Горизонтальний консольний стержень. 1. Викреслюємо в масштабі розрахункову схему стержня і вказуємо величини діючих навантажень та числові значення лінійних розмірів (рис
1. Викреслюємо в масштабі розрахункову схему стержня і вказуємо величини діючих навантажень та числові значення лінійних розмірів (рис. 2.6).
2. Опорні реакції в защемленні не визначаємо, а внутрішні зусилля визначаємо з умов рівноваги частини стержня з боку вільного краю.
Прикладені під кутом до осі стержня зосереджені сили розкладаємо на складові, проектуючи їх на вісь стержня (вісь х) та на перпендикуляр до осі (вісь z):
;
;
;
.
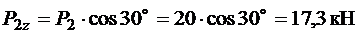3. Позначаємо характерні перерізи (1 – 4) вздовж осі стержня (рис. 2.6).
4. Обчислюємо величини та визначаємо знаки внутрішніх зусиль у зазначених точках стержня:
Рис. 2.6
а) поздовжня сила:
;
;
;
;
;
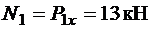б) поперечна сила:
кН;
кН;
кН;
кН;
кН;
в) згинальний момент:
;
кНм;
кНм;
кНм;
кНм.
5. За визначеними ординатами будуємо епюри (рис. 2.6).
6. Правильність побудови епюр перевіряємо за диференціаль-ними залежностями між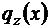 
, 
та 
:
1) розподілене навантаження на стержень відсутнє (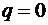 
), тому тангенс кута нахилу дотичної до епюри також рівний 0 і епюра по всій довжині стержня обмежена відрізками прямих, паралельних базі (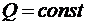 
); оскільки 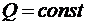, епюра обмежена відрізками прямих;
2) перевіряємо перерізи в точках прикладення зосередженого навантаження. В цих точках епюри мають стрибок, абсолютна величина якого дорівнює величині зосередженого навантаження:
;
;
.
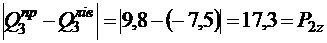ПРИКЛАД 2.5
Стержень на трьох шарнірних опорах
|
|
|
1. Викреслюємо в масштабі розрахункову схему стержня і вказуємо величини діючих навантажень та числові значення лінійних розмірів (рис. 2.7).
Рис. 2.7
2. Опори умовно відкидаємо і заміняємо їх дію опорними реакціями. Перерізи В, С, D закріплені шарнірно-рухомими опорами, реакції в яких направлені перпендикулярно опорним площинам (рис. 2.7).
Реакції опор визначаємо з рівнянь рівноваги стержня. У даному випадку рівняння мають такий вигляд:
;
;
кН;
кН.
Перевірка:
.
Прикладені під кутом до осі стержня опорні реакції розкладаємо на складові, проектуючи їх на вісь стержня (вісь х) та на перпендикуляр до осі (вісь z):
;
.
3. Позначаємо характерні перерізи (В – Е) вздовж осі стержня (рис. 2.7).
4. Обчислюємо величини та визначаємо знаки внутрішніх зусиль у зазначених перерізах стержня:
а) поздовжня сила:
;
;
;
;
;
.
б) поперечна сила:
кН;
кН;
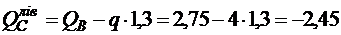кН;
кН;
кН;
;
.
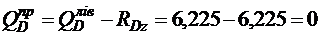в) згинальний момент:
Оскільки поперечна сила в межах ділянки В – С змінює знак, необхідно визначити координату перерізу, в якому 
, а згинальний момент набуває екстремального значення:
м;
кНм;
;
кНм;
;
кНм.
5. За визначеними ординатами будуємо епюри (див. рис. 2.7).
6. Правильність побудови епюр перевіряємо за диференціальними залежностями між 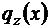, та :
|
|
|
1) на ділянці В – С 
, отже тангенс кута нахилу дотичної до епюри постійний і дорівнює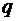 
, тобто епюра обмежена відрізком прямої, нахиленої до бази; оскільки змінюється за лінійним законом, тобто змінним є тангенс кута нахилу дотичної до епюри , то епюра у межах цієї ділянки обмежена квадратною параболою;
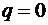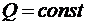2) на ділянці С – D , тому тангенс кута нахилу дотичної до епюри також рівний 0 і епюра обмежена відрізками прямих, паралельних базі ( ); оскільки 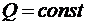, епюра у межах цих ділянок обмежена відрізками прямих;
3) перевіряємо перерізи в точках прикладення зосередженого навантаження. У цих точках епюри мають стрибок, абсолютна величина якого дорівнює величині зосередженого навантаження:
;
;
;
.
ПРИКЛАД 2.6
Дата добавления: 2018-02-18; просмотров: 1370; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!