Побудова епюр внутрішніх зусиль
МІНІСТЕРСТВО ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ
Київський національний університет будівництва і архітектури
ОПІР МАТЕРІАЛІВ
Геометричні характеристики плоских поперечних перерізів
Побудова епюр внутрішніх зусиль
Методичні рекомендації, завдання та приклади
до виконання розрахунково-графічних робіт
для студентів, які навчаються за напрямом підготовки
6.060101 „Будівництво”
| |
УДК 539.3
ББК 30.121
О-61
Укладачі: А. М. Станкевич, кандидат технічних наук, доцент
І. В. Жупаненко, кандидат технічних наук
Д. В. Левківський, асистент
Рецензент Л. Т. Шкельов, кандидат технічних наук, професор
Відповідальний за випуск А. М. Станкевич, кандидат технічних наук, доцент
Затверджено на засіданні кафедри опору матеріалів, протокол № 11 від 16 травня 2012 року.
Опірматеріалів. Геометричні характеристики плоских поперечних
О-61 перерізів. Побудова епюр внутрішніх зусиль: методичні рекомендації, завдання та приклади до виконання розрахунково-графічних робіт / уклад: А. М. Станкевич, І. В. Жупаненко, Д. В. Левківський. – К.: КНУБА, 2012. – 68 с.
Методичні рекомендації містять варіанти індивідуальних завдань, вказівки та детальні плани виконання розрахунково-графічних робіт з курсу «Опір матеріалів», а також приклади розв'язання кожного завдання. Розглянуто розділи: «Геометричні характеристики плоских поперечних перерізів» та «Побудова епюр внутрішніх зусиль».
|
|
|
Призначенодлястудентів, які навчаються за напрямом підготовки 6.060101 «Будівництво» для практичного використання під час виконання розрахунково-графічних робіт.
| |
Загальні положення
Методичні рекомендації призначені допомогти студентам виконати розрахунково-графічні роботи з курсу „Опір матеріалів” за розділами:
- „Геометричні характеристики плоских поперечних перерізів”;
- „Побудова епюр внутрішніх зусиль”.
Кожну розрахунково-графічну роботу студент повинен виконати за індивідуальним завданням, умова якого визначається згідно з шифром, виданим викладачем. Вихідні дані (розрахункові схеми та числові значення) студент вибирає з додатків (див. дод. 1, 2) за власним шифром у вигляді тризначного числа.
Оформлюється розрахунково-графічна робота на аркушах формату А4, які скріплюються зліва. Титульний аркуш роботи оформлюється за зразком:
Міністерство освіти і науки, молоді та спорту України
Київський національний університет будівництва і архітектури
Кафедра опору матеріалів
Розрахунково-графічна робота №___
|
|
|
„________________________________”
/тема/
Виконав:
студент_________________________
/спеціальність, курс, група/
_________________________
/прізвище, ініціали/
Керівник _______________________
/прізвище, ініціали/
Київ – 20__ р.
Пояснення та розрахунки потрібно виконувати на одній стороні аркуша ручкою, а креслення – олівцем. Дозволяється комп’ютерне виконання креслень.
Для кожного завдання наведено план та рекомендації щодо виконання поетапного розрахунку. Для ілюстрації наведено приклади виконання кожної РГР. Виконуючи кожен етап розрахунків, потрібно спочатку записати розрахункові формули, підставити числові значення та записати результат обчислення у відповідних одиницях виміру (см2, см3, см4, кН, кНм).
Розрахунково-графічна робота вважається зарахованою після її захисту.
Геометричні характеристики плоского поперечного перерізу
Постановка задачі
Для заданого поперечного перерізу, який складається з трьох елементів, потрібно визначити головні моменти інерції та моменти опору площі поперечного перерізу.
Вихідні дані
За особистим шифром із дод. 1 вибрати номери прокатних елементів, розміри пластини та розрахункову схему перерізу.
План виконання роботи
|
|
|
1. Відповідно до заданої схеми окремо накреслити кожен елемент складеного перерізу та виписати (або обчислити) усі вихідні геометричні характеристики кожного елемента.
2. Обрати допоміжну систему координат та визначити положення центра ваги складеного поперечного перерізу. Виконати перевірки.
3. Обчислити осьові та відцентровий моменти інерції перерізу відносно знайдених центральних осей.
4. Визначити величину та знак кута повороту, на який потрібно повернути центральну систему координат до набуття нею положення головної.
5. Обчислити головні центральні моменти інерції.
6. Обчислити головні радіуси інерції та побудувати еліпс інерції.
7. Користуючись побудованим еліпсом інерції, перевірити значення раніше обчислених моментів інерції відносно центральних осей.
8. Обчислити моменти опору площі складеного перерізу.
Рекомендації до виконання РГР
1. До складу перерізу, що розглядається, можуть входити: пластина (прямокутник), двотавр, швелер, кутик.
Кожен елемент перерізу, відповідно до завдання, потрібно накреслити окремо. На перерізі вказати центр ваги та положення власної центральної системи координат елемента, яка повинна мати напрямок та назву осей, що відповідають прийнятим у лекційному курсі. Для кожного елемента перерізу поруч із кресленням виписати лінійні розміри та необхідні геометричні характеристики. Користуючись таблицями сортаменту прокатної сталі, особливу увагу потрібно звернути на відповідність центральних систем координат елемента у завданні та сортаменті. Також потрібно пам’ятати, що відцентровий момент інерції для перерізів, які мають хоча б одну вісь симетрії, дорівнює нулю. Для кутиків, крім осьових моментів інерції, потрібно також виписати значення головних 
та 
моментів інерції, а величину відцентрового моменту інерції визначити за формулами:
|
|
|
- для рівнобічного кутика:
;
- для нерівнобічного кутика:
.
Знак відцентрового моменту інерції відповідає знаку квадрантів, у яких зосереджена більша частина площі поперечного перерізу. Визначення знака відцентрового моменту інерції кутика проілюстровано на рис. 1.1.
|
|
|
|
|
Рис.1.1
2. Положення центра ваги складеного перерізу визначається у допоміжній системі координат 
. Допоміжна система координат обирається дотичною до контуру перерізу, а сам переріз повинен знаходитись у додатному квадранті. Координати центра ваги визначаються за формулами:
; 
,
де 
– статичний момент площі перерізу відносно допоміжної осі 
;
– статичний момент площі перерізу відносно допоміжної осі 
;
– площа перерізу окремого елемента;
та 
– координати центрів ваги елементів у допоміжній системі координат.
Після визначення положення центра ваги складеного поперечного перерізу, його потрібно нанести на загальне креслення та виконати перевірки: візуальну (графічну) та математичну. Завдяки візуальній (графічній) перевірці переконуємось, що центр ваги складеного перерізу знаходиться усередині трикутника, вершинами якого є центри ваги елементів перерізу. Остаточною (математичною) перевіркою буде обчислення статичних моментів площі усього перерізу відносно знайдених центральних осей. Відповідно до визначення вони повинні дорівнювати нулю:
, 
,
де 
, 
– відстані між центральними та власними осями кожного елемента перерізу: – відстань між осями 
та з урахуванням знака, а – відстань між осями 
та . Похибка при обчисленні статичних моментів не повинна перебільшувати 
. Для забезпечення точності потрібно враховувати три знаки після коми.
3. Визначення осьових та відцентрового моментів інерції складеного перерізу відносно його центральної системи координат виконується за формулами паралельного переносу:
,
,
,
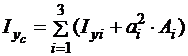де 
– значення власних осьових та відцентрового моментів інерції кожного елемента перерізу. Під час аналізу отриманих результатів потрібно пам’ятати, що значення осьових моментів інерції завжди додатні, а знак відцентрового моменту інерції можна перевірити за раніше згаданим правилом (для кутика).
4. Положення головної центральної системи координат визначається кутом повороту центральної системи координат у ту чи іншу сторону залежно від знака кута. Кут повороту та його знак визначаються через тангенс подвійного кута за формулою:
.
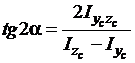У зв’язку з тим, що 
– функція непарна, значення кута може бути як додатним, так і від’ємним. Залежно від знака кута здійснюється поворот центральної системи координат. При 
поворот центральної системи координат здійснюємо за рухом годинникової стрілки, якщо 
– проти руху годинникової стрілки. Також потрібно пам’ятати, що 
(не існує), відповідно кут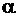 
може змінюватись лише у межах 
. Випадок, коли 
свідчить про те, що переріз має осі симетрії.
5. Головні центральні моменти інерції обчислюються за формулами:
;
,
а також
;
.
Потрібно пам’ятати, що головні моменти інерції є максимальним та мінімальним з можливих. Для перевірки їх визначення застосовують формулу, яка не містить тригонометричних функцій:
.
Також потрібно перевірити інваріантність суми осьових моментів інерції:
.
6. Обчислення головних радіусів інерції виконують за формулами:
Радіуси інерції використовуємо як півосі для побудови еліпса інерції, відкладаючи їх перпендикулярно однойменній осі, тобто 
. За допомогою еліпса інерції перевіряємо значення осьових моментів інерції 
та 
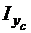. Для цього на осі та опускаємо дотично до еліпса перпендикуляри. Відрізки, які відсікають на осях ці перпендикуляри, будуть, відповідно, радіусами інерції 
та 
. Моменти інерції обчислюємо за формулами:
, 
.
Так, за допомогою еліпса інерції, можна визначити моменти інерції відносно будь-якої центральної системи координат.
7. Для обчислення моментів опору перерізу відносно головної системи координат потрібно визначити найбільш віддалені від кожної осі точки перерізу. Відстані від осей до точок вимірюються графічно на кресленні перерізу у відповідному масштабі. Моменти опору обчислюються за формулами:
, 
.
Тут 
та 
– відстані до найбільш віддалених точок від осі 
та 
відповідно.
ПРИКЛАД 1.1
Визначити головні центральні моменти інерції та моменти опору складеного поперечного перерізу, схема якого показана на рис. 1.2, побудувати еліпс інерції.
Рис. 1.2
1. Відповідно до заданої схеми окремо викреслюємо кожен елемент перерізу та визначаємо усі вихідні геометричні характеристики кожного елемента.
Для кутика і швелера геометричні характеристики виписуємо з таблиць сортаменту (ГОСТ 8240-72 та ГОСТ 8509-72), для пластини – обчислюємо за формулами прямокутника:
а) прямокутник 200х10 мм:
;
;
;
;
б) кутик рівнобічний 75х5:
;
;
;
;
;
в) швелер № 18 (з нахилом внутрішніх граней полиць) :
;
;
;
.
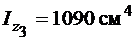Загальна площа поперечного перерізу:
.
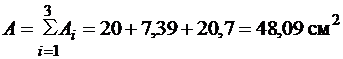2. Обираємо допоміжну систему координат та визначаємо положення центра ваги складеного поперечного перерізу.
Координати центра ваги визначаємо у допоміжній системі координат , яку обираємо дотичною до контуру перерізу так, щоб переріз знаходився у додатному квадранті.
Викреслюємо в масштабі схему поперечного перерізу, вказуємо положення центрів ваги і центральні осі кожного з елементів (рис. 1.3).
Рис. 1.3. Визначення центра ваги перерізу
Обчислюємо координати центрів ваги елементів у допоміжній системі координат 
, тобто відстані до центрів ваги кожного з елементів від допоміжних осей:
Координати центра ваги перерізу:
На схемі перерізу (рис. 1.3) від допоміжних осей відкладаємо координати центра ваги 
та 
і проводимо центральні осі.
Визначаємо координати центрів ваги кожного елемента перерізу в центральній системі координат 
, тобто відстані між центральними осями перерізу та власними центральними осями кожного елемента:
Для переконання у правильності визначення положення центра ваги складеного перерізу перевіряємо умову рівності нулю статичного моменту площі перерізу відносно центральних осей.
.
Відносна похибка складає:
.
.
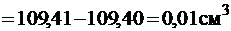Відносна похибка складає:
.
Відносні похибки обчислення не перевищують допустиме значення.
3. Обчислюємо осьові та відцентровий моменти інерції перерізу відносно знайдених центральних осей.
Осьові та відцентровий моменти інерції перерізу обчислюємо за формулами паралельного переносу:
Візуально перевіряємо знак “+” відцентрового моменту інерції перерізу. Як видно з рис. 1.3, більша частина площі перерізу знаходиться в І-й та ІІІ-й чвертях, тобто добуток координат центрів ваги цих частин додатній.
4. Визначаємо величину та знак кута повороту, на який потрібно повернути центральну систему координат до набуття нею положення головної.
; 
.
Проводимо головні осі перерізу u, v, повертаючи відповідно центральні осі 
та 
на кут 
в додатному напрямку (проти руху годинникової стрілки) (рис. 1.4).
Рис. 1.4
5. Обчислюємо головні центральні моменти інерції перерізу.
а) 
б) 
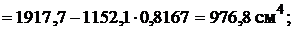
в) 
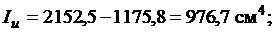
Таким чином отримали головні моменти інерції перерізу 
, 
. Оскільки 
, повертаючи на кут 
від осі , отримаємо вісь 
, а повертаючи від осі – вісь 
.
Перевіряємо умову інваріантності осьових моментів інерції:
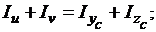
6. Обчислюємо головні радіуси інерції та будуємо еліпс інерції перерізу.
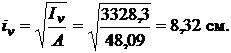
На головних центральних осях інерції будуємо еліпс з центром у центрі ваги перерізу і півосями, що дорівнюють головним радіусам інерції (рис. 1.4). При цьому радіуси інерції відкладаються перпендикулярно відповідній осі ( 
, 
).
7. Користуючись побудованим еліпсом інерції, перевіряємо значення раніше обчислених моментів інерції відносно центральних осей.
Графічно визначаємо радіуси інерції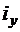 
та 
, для чого опускаємо на центральні осі дотичні до еліпса перпендикуляри і вимірюємо довжини відрізків, які перпендикуляри відсікають на осях ,
(рис. 1.4): 
, 
.
;
.
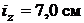8. Обчислюємо головні моменти опору складеного перерізу.
За рис. 1.4 визначаємо відстані від найбільш віддалених точок перерізу до осей и та v. Найбільш віддалена від осі v точка А ( 
), а від осі и – точка В ( 
).
Обчислюємо головні моменти опору перерізу:
; 
.
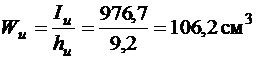ПРИКЛАД 1.2
Для поперечного перерізу, схема якого показана на рис. 1.5, визначити моменти інерції 
, 
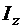та 
.
1. Переріз розбиваємо на три окремі елементи (прості фігури):
-
|
і висотою 
;
- трикутник шириною і висотою ;
- вирізаний півкруг радіусом 
.
Для елементів перерізу визначаємо геометричні характеристики відносно власних центральних осей.
а) прямокутник:
;
;
;
.
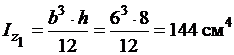б) трикутник:
;
;
;
.
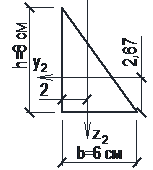
в) півкруг :
;
;
.
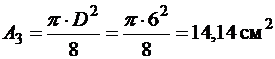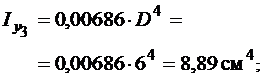
Оскільки півкруг вирізаний, його площу та моменти інерції в подальшому враховуємо зі знаком «–».
2. Задані осі у та z паралельні власним центральним осям елементів перерізу, тому моменти інерції перерізу відносно осей у та z обчислюємо за формулами паралельного переносу.
Знаходимо відстані між заданими осями та власними центральними осями елементів перерізу (рис. 1.6):
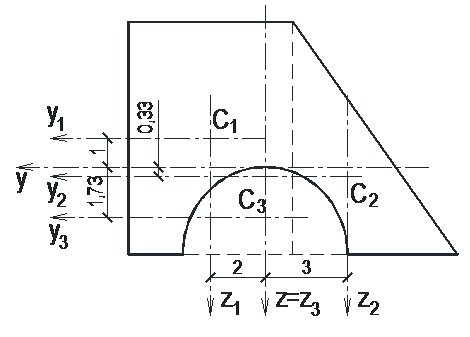
Рис. 1.6
ПРИКЛАД 1.3
Для поперечного перерізу, схема якого показана на рис. 1.7, визначити моменти інерції 
, 
та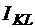 
.
|
а) двотавр № 24:
;
;
;
.
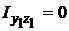б) кутик 100х10:
;
;
;
;
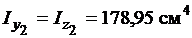2. Обчислюємо моменти інерції перерізу відносно допоміжних осей 
. Допоміжні осі (рис. 1.8) приймаємо паралельними власним центральним осям елементів перерізу з початком координат на перетині заданих осей L, K.
Рис. 1.8
Визначаємо відстані між допоміжними осями та власними центральними осями елементів перерізу (рис. 1.8):
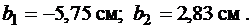
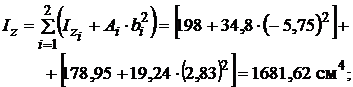
3. Обчислюємо моменти інерції перерізу відносно заданих осей LOK, повернутих відносно допоміжних осей за годинниковою стрілкою на кут 
:
Побудова епюр внутрішніх зусиль
Загальні зауваження
У перерізах довільно навантаженого стержня виникають внутрішні напруження. Зібрані по площі поперечного перерізу, вони характеризують внутрішні зусилля, що виникають у поперечних перерізах стержня. Для визначення внутрішніх зусиль у перерізі стержня застосовуємо „метод перерізів”. Він полягає у тому, що стержень умовно розрізається площиною на дві частини, кожна з яких знаходиться у рівновазі під дією зовнішнього навантаження та внутрішніх зусиль, які діють у площині поперечного перерізу. У загальному випадку в площині перерізу виникає головний вектор внутрішніх зусиль та головний момент.
У практичних розрахунках завжди використовуються проекції головного вектора та головного моменту на осі головної системи координат (рис. 2.1).
Рис. 2.1
Величини внутрішніх зусиль визначаються з умов рівноваги однієї з відсічених частин стержня.
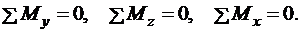
Для визначення дійсного напрямку внутрішнього зусилля потрібно з’ясувати його знак. Знак внутрішнього зусилля залежить від знаку нормалі до площини перерізу, що розглядається. Вважаємо, що нормаль буде додатною, якщо її напрямок співпадає з додатним напрямком відповідної осі. Тоді знаки внутрішніх зусиль потрібно визначати за таким правилом.
Поздовжнє – 
та поперечні – 
, 
внутрішні зусилля вважаються додатними, якщо у перерізі з додатною нормаллю їх напрямок співпадає з додатним напрямком відповідної осі.
Згинальні моменти 
та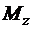 
вважаються додатними, якщо розтягують волокно стержня з додатного напрямку осі.
Момент кручення 
вважається додатним, коли з напрямку нормалі його поворот бачимо проти руху годинникової стрілки.
На рис. 2.1 вказані всі додатні напрямки внутрішніх зусиль у поперечному перерізі відсіченої частини стержня.
Постановка задачі
Для кожного стержня, заданого розрахунковою схемою, визначити величини та напрямки внутрішніх зусиль та побудувати їх епюри.
Вихідні дані
За особистим шифром з дод. 2 вибрати лінійні розміри стержня, величини навантажень та номер розрахункової схеми.
План виконання роботи
1. Відповідно до завдання, накреслити у масштабі розрахункову схему стержня. Вказати величини діючих навантажень та числові значення лінійних розмірів.
2. Обчислити величини діючих опорних реакцій.
3. Визначити характерні перерізи та вузлові точки вздовж осі стержня.
4. Обчислити величини та визначити знаки внутрішніх зусиль у зазначених точках стержня.
5. Побудувати епюри внутрішніх зусиль.
6. Перевірити правильність побудованих епюр.
Рекомендації до виконання РГР
1. У наведених в додатку схемах замість реального стержня зображено його вісь у вигляді лінії (прямої, ламаної або кривої), з літерними позначеннями довжин ділянок та прикладених навантажень. При складанні розрахункової схеми на її кресленні потрібно літерні позначення замінити на задані цифрові величини. Для уникнення спотворення характеру епюр, креслення обов’язково потрібно виконувати у масштабі.
У випадках, коли напрямок заданого навантаження не збігається з напрямками осей системи координат, потрібно визначити проекції цього навантаження на відповідні осі та вказати їх числові значення.
2. У заданих схемах стержнів зустрічаються такі види опор:
а) шарнірно-рухома опора – має одну в’язь, в якій виникає опорна реакція, перпендикулярна до опорної площини (рис. 2.2 а) або спрямована вздовж опорного стержня (рис. 2.2 б);
б) шарнірно-нерухома опора – має дві в’язі, в яких виникають дві лінійні опорні реакції – вздовж та перпендикулярно осі стержня
(рис. 2.2 в);
в) жорстке закріплення – обмежує можливість опори рухатись у двох напрямках та обертатись навколо точки опори. У такій опорі виникають дві лінійні реакції та реактивний (згинальний) момент (рис. 2.2.г).
а б в г
Рис. 2.2
У консольних стержнях (таких, що жорстко закріплені з одного краю) опорні реакції можна не визначати. Внутрішні зусилля у поперечних перерізах таких стержнів визначають, рухаючись з вільного краю (консолі) до жорсткого закріплення, розглядаючи завжди рівновагу відсіченої консольної частини стержня.
Для всіх інших варіантів закріплення стержнів потрібно визначати опорні реакції з умови статичної рівноваги стержня. Попередній напрямок опорних реакцій при складанні рівнянь рівноваги обирається довільно. Якщо у розрахунках знайдена реакція має від’ємний знак, це свідчить про її протилежний напрямок. На розрахунковій схемі потрібно вказувати тільки дійсні напрямки діючих навантажень та опорних реакцій.
Для балок із наскрізними шарнірами, крім звичайних рівнянь рівноваги потрібно додатково складати рівняння рівності нулю суми моментів усіх сил, що діють ліворуч або праворуч від шарніра:
або 
.
Також опорні реакції для балок із наскрізними шарнірами можна визначати, застосовуючи метод „поверхів”. Застосовуючи цей метод, потрібно завжди першою розглядати ту частину балки, яка внаслідок „розрізання” набуває степеня вільності.
3. Характерними перерізами (або точками) стержня є границі ділянок, у межах яких закон зміни внутрішніх зусиль залишається постійним. Відповідно, такими точками є:
- початок і закінчення стержня;
- точки, в яких прикладені зосереджені навантаження (сили, моменти, опорні реакції);
- точки початку, закінчення або зміни інтенсивності розподіленого навантаження;
- точки диференціальних залежностей.
Вузлом називаємо таку точку, в якій з’єднуються декілька стержнів або вісь стержня зламується, змінюючи напрямок. У вузлі стержня завжди потрібно перевіряти умову рівноваги.
4. Внутрішні зусилля у характерних перерізах можна обчислювати за допомогою складання рівнянь рівноваги відсіченої частини стержня. При складанні рівнянь для кожної ділянки стержня потрібно вказати границі зміни координати 
та, відповідно до наведених рекомендацій та правила знаків, скласти рівняння для кожного внутрішнього зусилля як функцію координати .
Складаючи рівняння, потрібно пам’ятати про існуючі диференціальні залежності між зовнішнім навантаженням та внутрішніми зусиллями:
,
, (2.1)
,
Отже, враховуючи диференціальні та інтегральні залежності між діючим навантаженням та внутрішніми зусиллями, можна впевнено визначити графік функції внутрішніх зусиль на кожній ділянці стержня. Виходячи з цього, більш раціональним є обчислення внутрішніх зусиль у характерних перерізах без складання рівнянь. Отримані результати використовуємо для побудови епюр внутрішніх зусиль.
5. Оскільки епюра внутрішнього зусилля – це графік, який відображає закон зміни величини та напрямку цього зусилля по довжині стержня, до епюри застосовують такі ж вимоги, як і до графіків. Епюри будують кожну окремо у масштабі на осьових лініях, які паралельні осі стержня (базах епюри). Обчислені у характерних перерізах значення 
є ординатами епюр відповідних внутрішніх зусиль. Ординати епюр відкладають перпендикулярно базі епюри у площині діючого навантаження. Обов’язковою є вимога будувати епюри згинальних моментів з боку розтягнутого волокна.
6. Перевірку правильності побудованих епюр виконуємо на основі диференціальних залежностей:
Характер діючого навантаження обумовлює вигляд епюр та :
- значення поперечної сили є тангенсом кута нахилу епюри згинальних моментів;
- знак епюри 
вказує на зростання або зменшення значень епюри згинальних моментів;
- нульові значення епюри вказують на наявність екстремумів в епюрі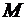 
.
Також потрібно пам’ятати, що у перерізах, де прикладені зосереджені сили, в епюрі відбуваються стрибки на величину та у напрямку діючої сили, а в епюрі 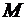– злами у напрямку діючої сили. Стрибки в епюрі 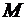відбуваються у точках прикладання зосереджених моментів.
Для перевірки епюр у стержнях, що мають вузлові точки, обов’язково потрібно розглядати умову рівноваги вузла.
ПРИКЛАД 2.1
Дата добавления: 2018-02-18; просмотров: 2244; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!