Связь между потенциалом и напряженностью электростатического поля.
Энергия взаимодействия системы точечных зарядов
Объемная плотность заряда
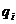
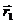Напомним, что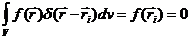 
Тогда энергия 
Так как 
Где 
- потенциал в точке i-го заряда, а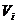 
- объем 
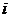-го заряда.
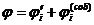
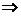
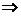
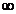
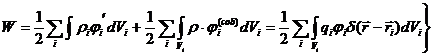Итак:
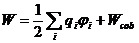Энергия взаимодействия
различных элементов
Энергия взаимодействия 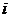-го заряда точечного заряда друг
с другими зарядами с другом
Таким образом, энергия взаимодействия точечных зарядов:
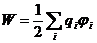
При этом для одного заряда q в точке с потенциалом φ энергия
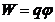- энергия заряда 
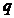в поле 
.
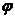Теорема Гаусса для вектора напряженности электростатического поля.
Общая формулировка: Поток вектора напряжённости электрического поля через любую произвольно выбранную замкнутую поверхность пропорционален заключённому внутри этой поверхности электрическому заряду.
| СГС | СИ |
| 
|
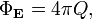
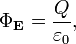
где
§ 
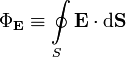— поток вектора напряжённости электрического поля через замкнутую поверхность S.
§ Q — полный заряд, содержащийся в объёме, который ограничивает поверхность S.
|
|
|
§ ε0 — электрическая постоянная.
Данное выражение представляет собой теорему Гаусса в интегральной форме.
§ Замечание: поток вектора напряжённости через поверхность не зависит от распределения заряда (расположения зарядов) внутри поверхности.
В дифференциальной форме теорема Гаусса выражается следующим образом:
| СГС | СИ |
| 
|
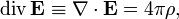
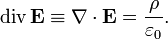
Здесь ρ — объёмная плотность заряда (в случае присутствия среды — суммарная плотность свободных и связанных зарядов), а 
— оператор набла.
§ Теорема Гаусса может быть доказана как теорема в электростатике исходя из закона Кулона (см. ниже). Формула однако также верна в электродинамике, хотя в ней она чаще всего не выступает в качестве доказываемой теоремы, а выступает в качестве постулируемого уравнения (в этом смысле и контексте ее логичнее называть законом Гаусса[2].
Дата добавления: 2018-02-18; просмотров: 619; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!