Вынужденные колебания. Амплитуда вынужденных колебаний
Вынужденные колебания — колебания, происходящие под воздействием внешних сил, меняющихся во времени.
Автоколебания отличаются от вынужденных колебаний тем, что последние вызваны периодическим внешним воздействием и происходят с частотой этого воздействия, в то время как возникновение автоколебаний и их частота определяются внутренними свойствами самой автоколебательной системы.
Наиболее простой и содержательный пример вынужденных колебаний можно получить из рассмотрения гармонического осциллятораи вынуждающей силы, которая изменяется по закону: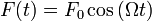 
.
Амплитуда вынужденных колебаний 7в 7стТ) и их фаза Y полностью определяются при заданных амплитуде внешней силы и декременте относительной частотой возбуждения. [1]
Амплитуда вынужденных колебаний этом случае увеличивается пропорционально времени. Круговая частота вынужденных колебаний при резонансе совпадает с круговой частотой возмущающей силы. [2]
Амплитуда вынужденных колебаний стремится к нулю быстрее при линейном сопротивлении с увеличением относительной частоты возмущающей силы, чем при отсутствии сопротивления. [3]
Амплитуды вынужденных колебаний равны абсолютным значениям А, и Av Воспользуемся формулой ( 7) для определения амплитуды М0 возмущающего момента. [4]
Амплитуда вынужденных колебаний зависит не только ( и не столько) от величины действующей силы, но и от ее частоты. Амплитуда вынужденных колебаний очень резко возрастает, если частота внешней силы близка к частоте собственных колебаний. [5]
|
|
|
Амплитуда вынужденных колебаний не зависит от начальных условий. Но она не зависит также и от времени, а потому вынужденные колебания с течением времени не угасают. [6]
Амплитуда вынужденных колебаний зависит еще и от силы трения. [7]
Амплитуда вынужденных колебаний получается путем умножения статической амплитуды на этот коэффициент. При равенстве частот ш и р наступает явление резонанса. Если сопротивления среды нет, и 0 ( идеальный случай), резонансная, амплитуда будет равна бесконечности. [8]
Амплитуда вынужденных колебаний стремится к нулю быстрее при линейном сопротивлении с увеличением относительной частоты возмущающей силы, чем при отсутствии сопротивления. [9]
Амплитуда вынужденных колебаний в этом случае увеличивается пропорционально времени. Круговая частота вынужденных колебаний при резонансе совпадает с круговой частотой возмущающей силы. [10]
Амплитуда вынужденных колебаний стремится к нулю быстрее при линейном сопротивлении с увеличением относительной частоты возмущающей силы, чем при отсутствии сопротивления. [11]
Амплитуда вынужденных колебаний зависит от величины потерь энергии вибрирующими подвижными частями прибора при постоянстве всех прочих условий. Эти потери обусловливаются вязкостью жидкости, деформацией пружинящих лент и трением в воздухе. [12]
|
|
|
Амплитуда вынужденных колебаний от начальных условий не зависит. Вынужденные колебания при наличии сопротивления не затухают. [13]
Амплитуда вынужденных колебаний пропорциональна амплитуде внешнего воздействия. [14]
Функция распределения молекул по скоростям
Скорости молекул газа имеют различные значения и направления, причем из-за огромного числа соударений, которые ежесекундно испытывает молекула, скорость ее постоянно изменяеться. Поэтому нельзя определить число молекул, которые обладают точно заданной скоростью v в данный момент времени, но можно подсчитать число молекул, скорости которых имеют значение, лежащие между некоторыми скоростями v1 и v2 . На основании теории вероятности Максвелл установил закономерность, по которой можно определить число молекул газа, скорости которых при данной температуре заключены в некотором интервале скоростей. Согласно распределению Максвелла, вероятное число молекул в единице объема; компоненты скоростей которых лежат в интервале от 
до 
, от 
до 
и от 
до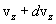 
, определяются функцией распределения Максвелла
|
|
|
где m - масса молекулы, n - число молекул в единице объема. Отсюда следует, чтсг число молекул, абсолютные значения скоростей которых лежат в интервале от v до v + dv, имеет вид
Распределение Максвелла достигает максимума при скорости 
, т.е. такой скорсти, к которой близки скорости большинства молекул. Площадь заштрихованной полоски с основанием dV покажет, какая часть от общего числа молекул имеет скорости, лежащие в данном интервале. Конкретный вид функции распределения Максвелла зависит от рода газа (массы молекулы) и температуры. Давление и объем газа на распределение молекул по скоростям не влияет.
Кривая распределения Максвелла позволит найти среднюю арифметическую скорость
.
Таким образом,
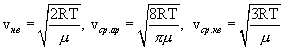
| (11.1) |
С Повышением температуры наиболее вероятная скорость возрастает, поэтому максимум распределения молекул по скоростям сдвигается в сторону больших скоростей, а его абсолютная величина уменьшается. Следовательно, при нагревании газа доля молекул, обладающих малыми скоростями уменьшается, а доля молекул с большими скоростями увеличивается.
|
|
|
Барометрическая формула
БАРОМЕТРИЧЕСКАЯ ФОРМУЛА - определяет зависимость от высоты h плотности n или давления pидеального изотермического газа, находящегося в гидростатическом равновесии в однородном поле силы тяжести. Высота h отсчитывается в направлении, противоположном ускорению силы тяжести g. Б. ф. явл. частным случаем Больцмана распределения, обычно используется для описания атмосфер космич. тел (планет, звёзд).
Дата добавления: 2018-02-18; просмотров: 2664; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!