Угловая скорость и угловое ускорение
Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени:
Вектор ω направлен вдоль оси вращения по правилу правого винта, т. е. так же, как и вектор dφ (рис. 2). Размерность угловой скорости dim ω = Т-1, а ее единица — радиан в секунду (рад/с).
Линейная скорость точки (см. рис. 1)
т.е
v=ωR
В векторном виде формулу для линейной скорости можно написать как векторное произведение:
При этом модуль векторного произведения, по определению, равен ωRsin(ω, R), а направление совпадает с направлением поступательного движения правого винта его вращения от ω к R.
Если ω=const, то вращение равномерное и его можно характеризовать периодом вращения Т - временем, за которое точка совершает один полный оборот, т. е. поворачивается на угол 2π. Так как промежутку времени Δt=Т соответствует Δφ=2π, то ω=2π/T, откуда
Т = 2π/ω.
Число полных оборотов, совершаемых телом при равномерном его движении по окружности, в единицу времени называется частотой вращения:
n= 1/T = ω/(2π),
откуда
ω = 2πn.
Угловым ускорением называется векторная величина, равная первой производной yгловой скорости по времени:
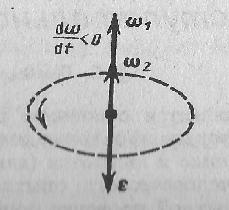
При вращении тела вокруг неподвижной оси вектор углового ускорения ε направлен вдоль оси вращения в сторону вектора элементарного приращения угловой скорости. При ускоренном движении вектор ε сонаправлен вектору ω (рис. 3), при замедленном - противонаправлен ему (рис. 4).
|
|
|
|
Нормальная составляющая ускорения 
Значит, связь между линейными (длина пути s, пройденного точкой по дуге окружности радиуса R, линейная скорость v, тангенциальное ускорение аτ, нормальное ускорение аn) и угловыми величинами (угол поворота φ, угловая скорость ω, угловое ускорение ε) выражается следующими формулами:
s = Rφ, v = Rω, аτ = R?, an = ω2R.
В случае равнопеременного движения точки по окружности (ω=const)
ω = ω0 ± ?t, φ = ω0t ± ?t2/2,
где ω0 — начальная угловая скорость.
Мгновенная ось вращения.
МГНОВЕННАЯ ОСЬ ВРАЩЕНИЯ
прямая, неподвижная в данный момент в нек-рой инерциальной системе отсчёта, относительно к-рой сложное движение твёрдого тела в этот момент можно представить как вращат. вокруг этой прямой. М. о. в. может лежать как внутри тела, так и вне его. С течением времени положение М. о. в. изменяется относительно как неподвижной системы отсчёта, так и системы отсчёта, движущейся вместе с телом.
Первый закон Ньютона и инерциальные системы отсчета
К выводу о существовании явления инерции впервые пришел Галилей, а затем Ньютон. Этот вывод формулируется в виде первого закона Ньютона (закона инерции): существуют такие системы отсчета, относительно которых тело (материальная точка) при отсутствии на нею внешних воздействий (или при их взаимной компенсации) сохраняет состояние покоя или равномерного прямолинейного движения.
|
|
|
Системы отсчета, в которых выполняется первый закон Ньютона, называют инерциальными. Следовательно, инерциальными являются такие системы отсчета, относительно которых материальная точка при отсутствии на нее внешних воздействий или их взаимной компенсации покоится или движется равномерно и прямолинейно.
Системы отсчета, в которых первый закон Ньютона не выполняется, называют неинерциальными. К таким системам относится любая система отсчета, движущаяся с ускорением относительно инерциальной системы отсчета.
Дата добавления: 2018-02-18; просмотров: 2530; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!