Теплоемкость идеальных газов.
Идеальный газ — математическая модель газа, в которой предполагается, что потенциальной энергией взаимодействия молекулможно пренебречь по сравнению с их кинетической энергией. Между молекулами не действуют силы притяжения или отталкивания, соударения частиц между собой и со стенками сосуда абсолютно упруги, а время взаимодействия между молекулами пренебрежимо мало по сравнению со средним временем между столкновениями.
Теплоемкость идеального газа — это отношение количества теплоты, сообщенного газу, к изменению температуры δТ, которое при этом произошло.

Молярная теплоемкость
Молярная теплоемкость — теплоемкость 1 моля идеального газа.
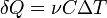

Уравнение адиабаты идеального газа.
Условие адиабатичности устанавливает, таким образом, дополнительную к
уравнению состояния связь между термодинамическими параметрами термоди-
намической системы. Поэтому в адиабатическом процессе состояние системы од-
нозначно определяется заданием одной переменной, например температуры. Ос-
тальные термодинамические величины будут функциями этой переменной. Чтобы
установить функциональную связь между термодинамическими параметрами
идеального газа в адиабатическом процессе или, как говорят на адиабате, необхо-
димо составить и решить несложное дифференциальное уравнение.
Пусть в результате малого изменения состояния идеального газа при адиаба-
|
|
|
тическом процессе (δQ = 0 ) температура газа изменилась на величину dT , а зани-
маемый газом объем изменился на величину dV . Из первого начала термодина-
мики в форме (3.5) и выражения (5.4) для внутренней энергии идеального газа
следует
C dT pdV V + = 0 . (6.1) 40
Привлекая уравнение состояния pV N k T = B
, исключаем из уравнения (6.1) давле-
ние p . Результат запишем в виде
dT
T
k N
C
dV
V
B
V
+ = 0 . (6.2)
Согласно (4.12) для идеального газа справедливо
k N C C B p V = − .
Теплоемкости CV и Cp
считаем постоянными. Введем обозначение
C
C
p
V
= γ (6.3)
С учетом (6.3), (6.4) из (6.2) следует
d lnT + d lnV = d lnTV =
γ γ − − 1 1
0 . (6.4)
Равенство нулю дифференциала функции означает, что функция есть константа.
Следовательно, на адиабате логарифм произведения TV
γ −1
сохраняет постоянное
значение. Постоянное значение сохраняет, стало быть, и само это произведение. В
итоге приходим к уравнению, связывающему на адиабате температуру и объем
идеального газа:
TV const
γ −
=
1
. (6.5)
Привлекая снова уравнение состояния идеального газа, можно записать уравне-
ний его адиабаты еще в других, эквивалентных (6.5), формах:
pV const
|
|
|
γ
= , (6.6)
Tpconstγγ−=1
. (6.7)
Энтропия. Второе начало термодинамики.
Энтропи́я (от греч. ἐντροπία — поворот, превращение) в естественных науках — мера беспорядкасистемы, состоящей из многих элементов. В частности, в статистической физике — меравероятности осуществления какого-либо макроскопического состояния; в теории информации — мера неопределённости какого-либо опыта (испытания), который может иметь разные исходы, а значит и количество информации; в исторической науке, для экспликации феноменаальтернативности истории (инвариантности и вариативности исторического процесса).
Второе начало термодинамики — физический принцип, накладывающий ограничение на направление процессов передачи тепла между телами.
Второе начало термодинамики гласит, что невозможен самопроизвольный переход тепла от тела, менее нагретого, к телу, более нагретому.
Второе начало термодинамики запрещает так называемые вечные двигатели второго рода, показывая что коэффициент полезного действия не может равняться единице, поскольку для кругового процесса температура холодильника не должна равняться 0.
Второе начало термодинамики является постулатом, не доказываемым в рамках термодинамики. Оно было создано на основе обобщения опытных фактов и получило многочисленные экспериментальные подтверждения.
Дата добавления: 2018-02-18; просмотров: 1320; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
