Кинетическая энергия твердого тела.
Консервативные и неконсервативные силы. Потенциальная сила.
В физике консервати́вные си́лы (потенциальные силы) — силы, работа которых не зависит от формы траектории (зависит только от начальной и конечной точки приложения сил). Отсюда следует определение: консервативные силы — такие силы, работа которых по любой замкнутой траектории равна 0.
Если в системе действуют только консервативные силы, то механическая энергия системы сохраняется.
Для консервативных сил выполняются следующие тождества:
§ 
— ротор консервативных сил равен 0;
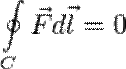— работа консервативных сил по произвольному замкнутому контуру равна 0;
§ 
— консервативная сила является градиентом некой скалярной функции U, называемой силовой. Эта функция равнапотенциальной энергии взятой с обратным знаком.
В физике силы разделяют на консервативные и неконсервативные. Примерами консервативных сил являются: сила тяжести, сила упругости. Примерами неконсервативных сил являются сила трения и сила сопротивления среды.
В теоретической физике выделяют только четыре типа сил, каждая из которых является консервативной.
Закон сохранения энергии в механике
Сумма кинетической и потенциальной энергии составляют полную механическую энергию системы Е
Т+П=Е (2.21)
Для замкнутых механических систем выполняется закон сохранения полной механической энергии
Т+П=Е=const (2.22)
Закон сохранения энергии – результат обобщения многих экспериментальных данных. Идея этого закона принадлежит М.В. Ломоносову (1711-1765), изложившему закон сохранения материи и движения, а количественная формулировка закона сохранения энергии дана немецким врачом Майером и немецким естествоиспытателем Гельмгольцем.
|
|
|
Гармонические колебания и их характеристики.
Как вы уже знаете, в природе существуют периодические и непериодические колебания. Особое место среди первых из них занимают гармонические колебания.
Гармоническими называются колебания, для которых изменяющаяся величина зависит от времени по закону синуса или косинуса.
Примеры: колебания груза на пружине при малой силе сопротивления, колебания маятника механических часов.
Уравнение гармонических колебаний можно записать в виде:
x = A*sin(wt +0), где
x - смещение точки от положения равновесия,
A - амплитуда колебаний,
(wt+0) - фаза колебаний,
0 - начальная фаза,
w - частота,
t - время.
Уравнение движения и энергия гармонического осциллятора.
Гармонический осциллятор (в классической механике) — это система, которая при смещении из положения равновесияиспытывает действие возвращающей силы 
, пропорциональной смещению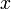 
(согласно закону Гука):
|
|
|
где k — положительная константа, описывающая жёсткость системы.
Если — единственная сила, действующая на систему, то систему называют простым или консервативным гармоническим осциллятором. Свободные колебания такой системы представляют собой периодическое движение около положения равновесия (гармонические колебания). Частота и амплитуда при этом постоянны, причём частота не зависит от амплитуды.
Если имеется ещё и сила трения (затухание), пропорциональная скорости движения (вязкое трение), то такую систему называютзатухающим или диссипативным осциллятором. Если трение не слишком велико, то система совершает почти периодическое движение — синусоидальные колебания с постоянной частотой и экспоненциально убывающей амплитудой. Частота свободных колебаний затухающего осциллятора оказывается несколько ниже, чем у аналогичного осциллятора без трения.
Если осциллятор предоставлен сам себе, то говорят, что он совершает свободные колебания. Если же присутствует внешняя сила (зависящая от времени), то говорят, что осциллятор испытывает вынужденные колебания.
Механическими примерами гармонического осциллятора являются математический маятник (с малыми углами отклонения), груз на пружине, торсионный маятник и акустические системы. Среди других аналогов гармонического осциллятора стоит выделить электрический гармонический осциллятор
|
|
|
Дата добавления: 2018-02-18; просмотров: 608; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!