Частотний критерій стійкості Найквіста
Критерій був розроблений американським вченим Найквістом у 1932 р. для дослідження електронних підсилювачів зі зворотним зв’язком. Пізніше він набув більшого використання для дослідження будь-яких САК. Перевагою його над іншими є те, що згідно з ним стійкість системи можна визначити як шляхом розрахунків, будуючи АФЧХ розімкнутих систем , так і експериментально, вимірюючи АФЧХ за допомогою приладів.
Критерій стійкості Найквіста формулюється таким чином: Замкнута САК є стійкою, якщо АФЧХ розімкнутої системи не охоплює точку –1 на дійсній осі комплексної площини (точку з координатами (-1, j0)). Ця умова є необхідною і достатньою для визначення стійкості САК.
Поняття розімкнутої системи ми вже розглядали. Це система, що являє собою повний ланцюжок зворотного зв’язку при умові його розриву в одному місці.
Приклади АФЧХ розімкнутих ланцюгів зворотного зв’язку стійких і нестійких систем показано на рис. 7.2.
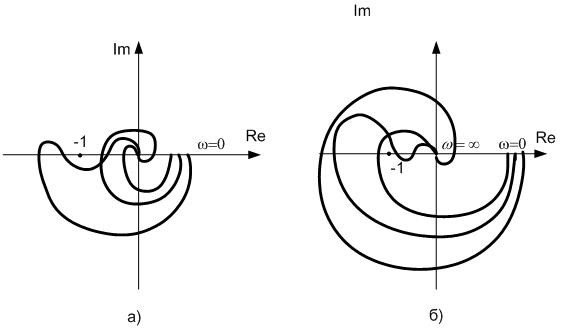
Рис. 7.2 – Приклади перевірки стійкості системи за критерієм Найквіста (АФЧХ розімкнутої системи: а- для стійких систем, б- для нестійких систем)
Для астатичних систем, систем, які мають у своєму складі інтегруючі ланки АФЧХ розімкнутої системи простягаються в нескінченність. Для того, щоб визначити стійкість такої системи, потрібно доповнити АФЧХ уявною дугою радіусом рівним безконечності до замикання з додатнім значенням дійсної осі. Стійкою вважається система для якої точка (-1, j0) поза виділеною частиною. Приклад таких САК показано на рис. 7.3.
 Рис. 7.3 – Приклади АФЧХ розімкнутої системи стійких астатичних САК
Рис. 7.3 – Приклади АФЧХ розімкнутої системи стійких астатичних САК
Логарифмічний частотний критерій стійкості Найквіста
Даний критерій дозволяє визначити стійкість системи шляхом співставлення амплітудної і фазової частотних характеристик.
Система стійка, якщо ЛАЧХ розімкнутої системи перетне вісь абсцис раніше ніж фаза пройде через значення -π.
Система стійка, якщо на частоті зрізу ЛАЧХ розімкнутої системи зсув фаз не перевищує -π (-1800).
Частотою зрізу називають частоту, при якій АФЧХ перетинає вісь абсцис.
Даний критерій – це той же критерій Найквіста, тільки в іншому формулюванні. Справді, якщо розглянути наведене раніше формулювання, то видно, що точка -1 за дійсною віссю відповідає амплітуді сигналу, рівній 1 і фазі –π (1800). Вісь абсцис на ЛАЧХ відповідає амплітуді сигналу рівній 1 (L = 20lg1 = 0). Фазі -π відповідає від’ємна частина дійсної осі. Всі точки в другому квадранті мають зсув фаз менший –π а в третьому квадранті – більший –π Отже якщо логарифм амплітуди буде від’ємним, коли фаза досягає –π, то це значить, що АФЧХ пройде через від’ємну частину дійсної осі між початком координат і точкою (-1, j0). АФЧХ розімкнутої системи не охопить точки (-1, j0), а значить система буде стійкою.
Запас стійкості
Про систему судять не тільки за тим стійкою, але за тим наскільки вона далека від нестійкого стану, який вона має запас стійкості. Система, якщо у неї недостатній запас стійкості, може перейти в нестійкий стан при зміні її параметрів. Такі зміни можуть виникнути з цілого ряду причин. Тому, крім стійкості системи характеризують запасом стійкості. Розрізняють цілий ряд параметрів, що характеризують запас стійкості системи. Ми розглянемо тільки два показники запасу стійкості, а саме запас стійкості за коефіцієнтом підсилення і за фазою.
Запас стійкості за коефіцієнтом підсилення. Збільшення коефіцієнта підсилення систем керування приводить до підвищення точності керування. Щоб підвищити точність керування завжди намагаються коефіцієнт підсилення системи зробити якомога більшим. Проте при збільшенні коефіцієнта підсилення система переходять зі стійкого стану в нестійкий. Тому для кожної системи намагаються забезпечити певний запас стійкості за коефіцієнтом підсилення. Характеристику запасу стійкості визначають кількістю децибел, на яку можна збільшити коефіцієнт підсилення системи, щоб вона досягла межі стійкості. Запас стійкості за коефіцієнтом підсилення визначають як відношення коефіцієнта підсилення системи, що знаходиться на межі стійкості, до фактичного коефіцієнта підсилення Для цього поряд з АФЧХ існуючої системи будують АФЧХ аналогічної системи із збільшеним коефіцієнтом підсилення. За виглядом АФЧХ визначають чи досяг коефіцієнт підсилення величини, при якій система знаходиться на межі стійкості. Коли коефіцієнт підсилення досягне граничного значення (АФЧХ пройде через точку -1, j0 комплексної площини), знаходять значення граничного коефіцієнта підсилення і обраховують запас стійкості за коефіцієнтом підсилення. На рис.7.4 показано приклад визначення запасу стійкості за коефіцієнтом підсилення.
Обраховують його згідно з формулою:
 . (7.8)
. (7.8)
Тут Кгр – коефіцієнт підсилення, при якому система досягає межі стійкості,
К – фактичне значення коефіцієнта підсилення стійкої системи.
Під час проектування САК рекомендується вибирати запас стійкості за коефіцієнтом підсилення не менше 6 дБ. h > 6 дБ.
Крім запасу стійкості за коефіцієнтом підсилення подекуди використовують такий показник, як запас стійкості за модулем. Запас стійкості за модулем АФЧХ визначають розміщенням точки перетину АФЧХ з дійсною віссю комплексної площини (див. рис.7.5).

Рис.7.4 – Визначення стійкості системи за коефіцієнтом підсилення

Рис. 7.5 – Загальний вигляд початкової частини АФЧХ розімкнутої системи.
Визначають його згідно з тією ж АФЧХ, як відносне значення модуля АФЧХ при перетині від’ємної частини дійсної осі. Величину запасу стійкості за модулем визначають згідно з формулами:
 (7.9)
(7.9)
Запас стійкості за фазою визначають за величиною зміщення за фазою, на яку величину повинно зрости запізнення за фазою, щоб стійка система виявилась на межі стійкості. Запас стійкості можна визначити за АФЧХ розімкнутої системи, який будується під час визначення стійкості системи згідно з критерієм Найквіста.
Для визначення запасу стійкості за фазою можна використати цю ж АФЧХ розімкнутої системи. Для визначення його проводять дугу з центром в початку координат через точку -1 до перетину з годографом. Запас стійкості визначають як кeт, на який потрібно повернути АФЧХ, щоб вона пройшла через точку -1 на дійсній осі. Тобто це кут між напрямком на точку перетину з проведеною дугою та від’ємним напрямком дійсної осі:
 (7.10)
(7.10)
Приклад визначення запасу стійкості за фазою показано на рис 7.5 та рис.7.6.
Для проектування САК рекомендується, щоб запас стійкості за фазою був не менше 300 Δφ > 300.
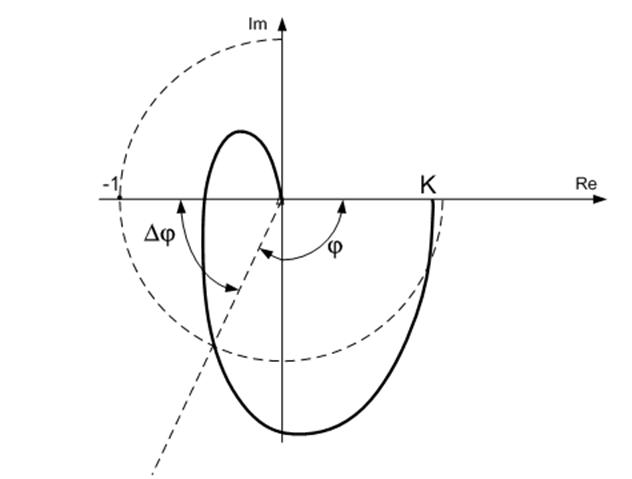
Рис.7.6 – Визначення стійкості системи за фазою
Більш зручним і наглядним є визначення запасу стійкості за логарифмічними частотними характеристиками розімкнутої системи. На рис.7.7 показано приклад логарифмічних частотних характеристик певної системи. Як видно з рисунка, запас стійкості за коефіцієнтом підсилення може бути визначений як віддаль в децибелах від осі ординат до графіка ЛФЧХ на частоті, при якій кут зсуву фаз дорівнює –π (1800). Запас стійкості за фазою згідно з цими ж характеристиками визначається різницею між фазою –π (1800). і величиною фази на частоті зрізу. Частотою зрізу називають частоту, при якій АФЧХ перетинає вісь абсцис (значення модуля АФЧХ дорівнює 1).

Рис 7.7 – Визначення запасу стійкості системи за логарифмічними частотними характеристиками
Дата добавления: 2018-02-15; просмотров: 1503; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
