Уравнение Клапейрона – Менделеева
Как уже отмечалось (п. 2.1 данного приложения), путём обобщения экспериментальных данных было получено уравнение состояния идеального газа (1). Учитывая определение удельного объёма его можно переписать в виде:
или р V = M R T, (8)
где V – объём газа, м3; M – масса газа, кг.
Соотношение (8) справедливо всегда, в частности, оно будет выполняться для одного киломоля некоторого идеального газа, находящегося при нормальных условиях. Для такого случая, исходя из (8), можно записать:
, (9)
где ро и То – нормальные давление и температура соответственно
ро = 101325 Па, То = 273,15 К; 
– объём, который занимает один киломоль идеального газа при н.у. = 22,4 м3; М1 – масса одного киломоля газа, кг.
Значение массы одного киломоля (103 молей) газа определяется по (2) (см. п. 2.2) следующим образом:
М1 = μ · 1 · 103, (10)
где μ – молярная масса газа, кг/моль.
Подставляя (10) в (9) получаем:
или 
. (11)
Подставляя в (11) известные численные значения для ро, и То, получаем:
, Дж/(кг · К). (12)
Размерность у числа 8,314, стоящего в числителе (12) Дж/(моль · К). Это число обозначается буквой Rμ, Дж/(моль · К), и называется универсальной газовой постоянной.
С учётом такого обозначения вместо (12) можно записать:
, Дж/(кг · К). (13)
|
|
|
Формула (13) позволяет определить значение газовой постоянной R для любого газа или газовой смеси, не прибегая к экспериментам, так как μ всегда известна.
Подставляя (13) в (1) окончательно получаем уравнение состояния идеального газа в виде формулы Менделеева – Клапейрона
. (14)
Приложение 3
Смеси идеальных газов
В технике часто расчёты проводятся не для чистых газов, а для газовых смесей.
Смесь идеальных газов можно рассматривать как идеальный газ, для которого уравнение состояния записывается в виде:
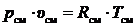или 
, (1)
где рсм, υсм и Тсм – параметры состояния смеси – абсолютное давление, удельный объём и температура, соответственно, Па, м3/кг, К; Rсм – газовая постоянная смеси, Дж/(моль · К); Rμ – универсальная газовая постоянная, Rμ = 8,314 Дж/(моль · К); μсм – кажущаяся молярная масса смеси, кг/моль.
Чтобы иметь возможность проводить расчёты с использованием уравнения (1) необходимо знать значения величин υсм, Rсм, μсм.
Эти значения всегда рассчитываются по известному химическому составу газовой смеси, который по условиям задачи всегда задан. (На практике он определяется с помощью газоанализатора).
|
|
|
Парциальные давления в газовой смеси. Закон Дальтона
Газовая смесь находится в состоянии равновесия, если её параметры состояния во всём объёме имеют одинаковые значения. При этом температура всех газов, входящих в смесь, одинакова и равна температуре смеси Тсм.
В равновесном состоянии молекулы каждого газа рассеяны равномерно по всему объёму смеси, то есть имеют свою определённую концентрацию и, следовательно, своё давление рi, Па, которое называется парциальным. Из этой констатации вытекает следующее определение.
Парциальное давление равно давлению данного компонента при условии, что он один занимает весь объём, предназначенный для смеси при температуре смеси Тсм.
По закону английского химика и физика Дальтона, сформулированному в 1801 году, давление смеси идеальных газов рсм равно сумме парциальных давлений её компонентов рi:
, (2)
где n – число компонентов.
Выражение (2) также называется законом парциальных давлений.
Дата добавления: 2018-02-15; просмотров: 1025; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!