Моделирование случайных событий и групп событий.
Одно событие:
Событие-факт,кот может происходить или не происходить. Надо смоделир наступление события во времени.
Введ в рассмотрение нов событие  Выч-им вер-ть Z:
Выч-им вер-ть Z:

 -случ вел-на,р-константа
-случ вел-на,р-константа
Xи Z-равносильн случайные величины
Алгоритм:
1)генерир 
2)сравниваем с р
3)если да,то событие Z и Х произошло
Группа событий:
 -независ события
-независ события


События образуют полн группу событий. Они попарно не совместны. В люб момент вр может произойти только одно событие.
Также будем генерир-ть базов послед-ть  ,распределён в диапазоне (0;1) равномерно. Можем рассм n событий.
,распределён в диапазоне (0;1) равномерно. Можем рассм n событий.
Напр,i –ое событие состоит в том, что  попало в i –ый отрезок,т.е
попало в i –ый отрезок,т.е


Z и Х-равносильн события
Алгоритм:
1)генерир 
2)определ, в какой отрезок попало 
3)№ отрезка и есть № произошед-го события
4)повтор процедуру нужное кол-во раз
Методы моделирования СВ.
-дискретные;
-непрерывные;
Чтобы генерировать нужно знать закон распределения. Он может быть записан в виде функции плотности либо в виде функций распределения вероятности.
Для имитации СВ исп
1) универсальные методы (генерация по закону) в частности метод обр. функций.
2) Исп спец методы (норм, гаусса, экспоненц…)
Метод обратных функций. Моделирование дискретных случайных велечин.
Могут задаваться ф-ией плотности(гистограммой) либо ф-ей распределения. Если вел-на явл дискретной, то использ график (табличные значения) ф-ции распред. При этом непрер вел-на сводится к дискретной.
|
|
|

показана ф-ция распред дискретной случ вел-ны (  = 1). Так, знач вел-ны Х- x1x2,...,xn можно поставить в соотв вероятн р ,р ,...,р , рассчит по зн-ниям ф-ции распр-ния как
= 1). Так, знач вел-ны Х- x1x2,...,xn можно поставить в соотв вероятн р ,р ,...,р , рассчит по зн-ниям ф-ции распр-ния как
р  =Fx(x
=Fx(x  )-Fx(xk-1). Указанные зн-ния X образ полн группу событий X = х
)-Fx(xk-1). Указанные зн-ния X образ полн группу событий X = х  , ...,Х= х
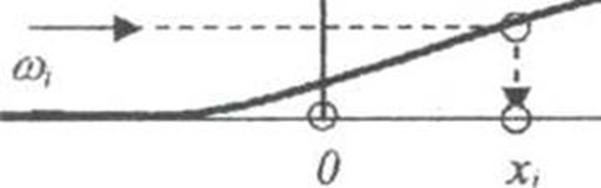
, ...,Х= х  , а задача генерации сводится к задаче моделир полн группы независ элементарных событий и графич означает "набрасывание" случ числа
, а задача генерации сводится к задаче моделир полн группы независ элементарных событий и графич означает "набрасывание" случ числа  , на отрезок ед длины по оси О- Y.
, на отрезок ед длины по оси О- Y.
Метод обратных функций.Моделирование непрерывных случайных велечин.
Пусть требуется имитир зн-ия случ в-ны X, для кот задан з-н распред, напр, в виде ф-ии распред Fx(x) = Р{Х < х). Если вел-на непрерывная и ф-ия распр-ия задана аналит, в виде ф-лы, то можно применить метод обратной ф-ции  , позвол через ее знач w определить зн-ие аргумента, т.е. Fx{x)=w
, позвол через ее знач w определить зн-ие аргумента, т.е. Fx{x)=w  x=Fx-1 (w). Если будет получено аналит выр-ие обр ф-ии, то алгоритм генерации сост в след: генерир зн-ние w
x=Fx-1 (w). Если будет получено аналит выр-ие обр ф-ии, то алгоритм генерации сост в след: генерир зн-ние w  , и рассчит очередное зн-ние
, и рассчит очередное зн-ние  по фор-ле xi=Fx-1 (wi). Напр, для равноме распредел величин из ф-ции распред по ф-ле (х - a)/(b - а)=w получают выр-ние =>хi=wi (b-a)+ а для аналитич расчета зн-ий x
по фор-ле xi=Fx-1 (wi). Напр, для равноме распредел величин из ф-ции распред по ф-ле (х - a)/(b - а)=w получают выр-ние =>хi=wi (b-a)+ а для аналитич расчета зн-ий x 
Моделирование типовых распределений (равномерного, показательного, Гаусса и др.).
|
|
|
1.Равномерное распределение
Пусть задана ф-ия распределения
 , т е a и b – заданы
, т е a и b – заданы
 =w
=w  x-?
x-?
X=w(b-a)+a
2.Показательное распределение


Если рассм поведение объекта во времени, то X может рассм как 1/t, где t – время м/у сосед событиями, а  - интенсивность появления событий, X – конкретное зн-ие времени м/у событиями
- интенсивность появления событий, X – конкретное зн-ие времени м/у событиями
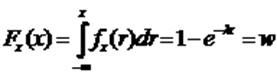
 x - ?
x - ?




Поскольку w  (0,1), то вел-на(1-w) обладает тем же самым з-ном. Поэтому
(0,1), то вел-на(1-w) обладает тем же самым з-ном. Поэтому 
Алгоритм аналогичный
3.Распределение Гаусса
Используем центр. предельную теорему , кот док-ет , что з-ном распределения случ вел-ны Z будет нормальный з-н

 ,x
,x  …x
…x  - независимы , равновесны , обладают тем же з-ном распределения
- независимы , равновесны , обладают тем же з-ном распределения
 и D
и D  - одинаковы
- одинаковы
а) генерир некот кол-вослуч вел-н , подчин этим условиям
б)суммируем их и масштабируем их , чтобы получить нормальное распределение с mx и Dx
Дата добавления: 2018-02-15; просмотров: 776; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
