Приведение силы к заданному центру

(теорема Пуансо)

 

 

Теорема. Силу F, не изменяя её действие на тело, можно перенести из точки её приложения А в любой центр приведения О, присоединив при этом к телу пару сил с моментом М, геометрически равным моменту M_О(F) этой силы относительно центра приведения.

 

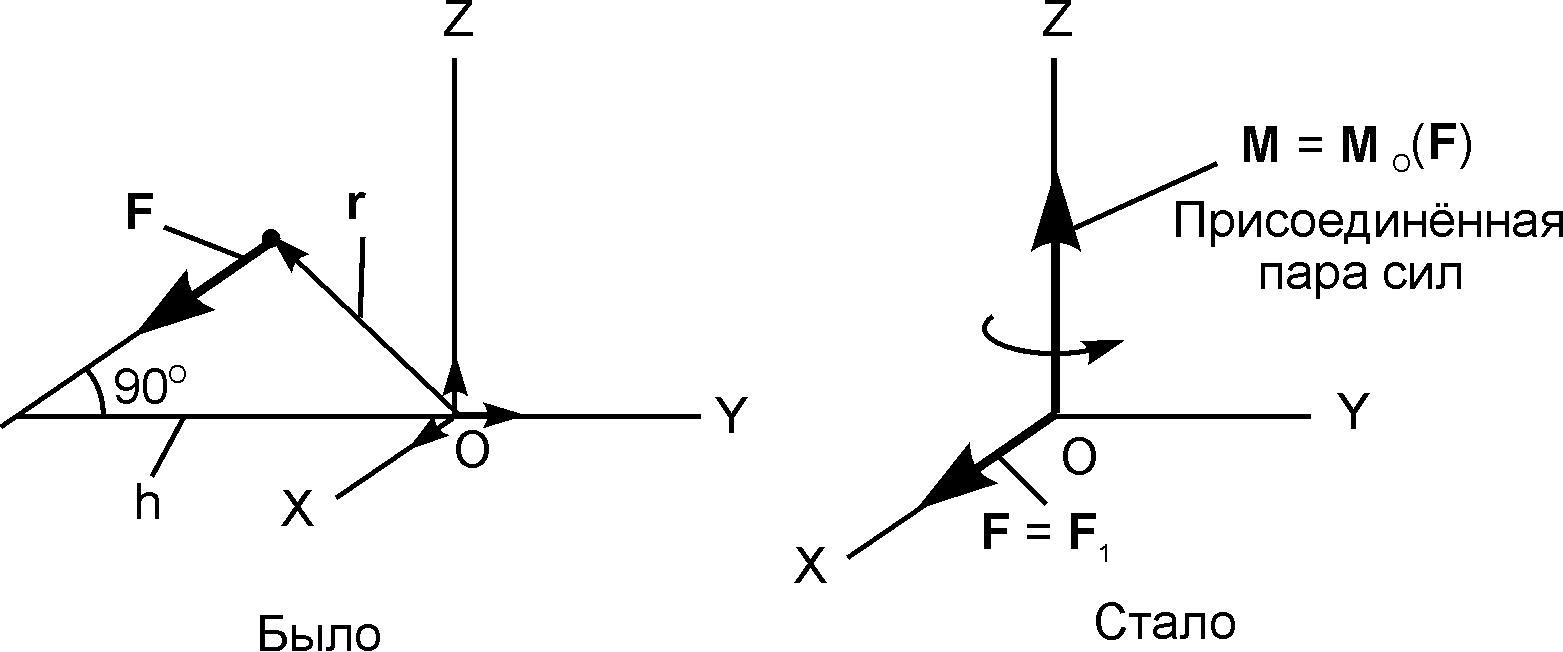Рис. 1.41

Пусть задана сила F, лежащая в горизонтальной плоскости OXY параллельно оси ОХ (рис. 1.41).

Согласно методу Пуансо вместо силы F, приложенной в точке А, получена сила F₁, равная по величине силе F, но приложенная в точке О и присоединённая пара сил, векторный момент которой M = M_О(F).

По теореме об эквивалентности пар сил присоединённую пару сил можно заменить любой другой парой сил с таким же векторным моментом.

 

 

Приведение произвольной системы сил

К заданному центру (теорема о главном векторе и главном моменте)

 

 

Теорема. Любую произвольную систему сил, действующую на тело, можно привести в общем случае к силе и паре сил.

 

Такой процесс замены системы сил одной силой и парой сил называют приведением системы сил к заданному центру.

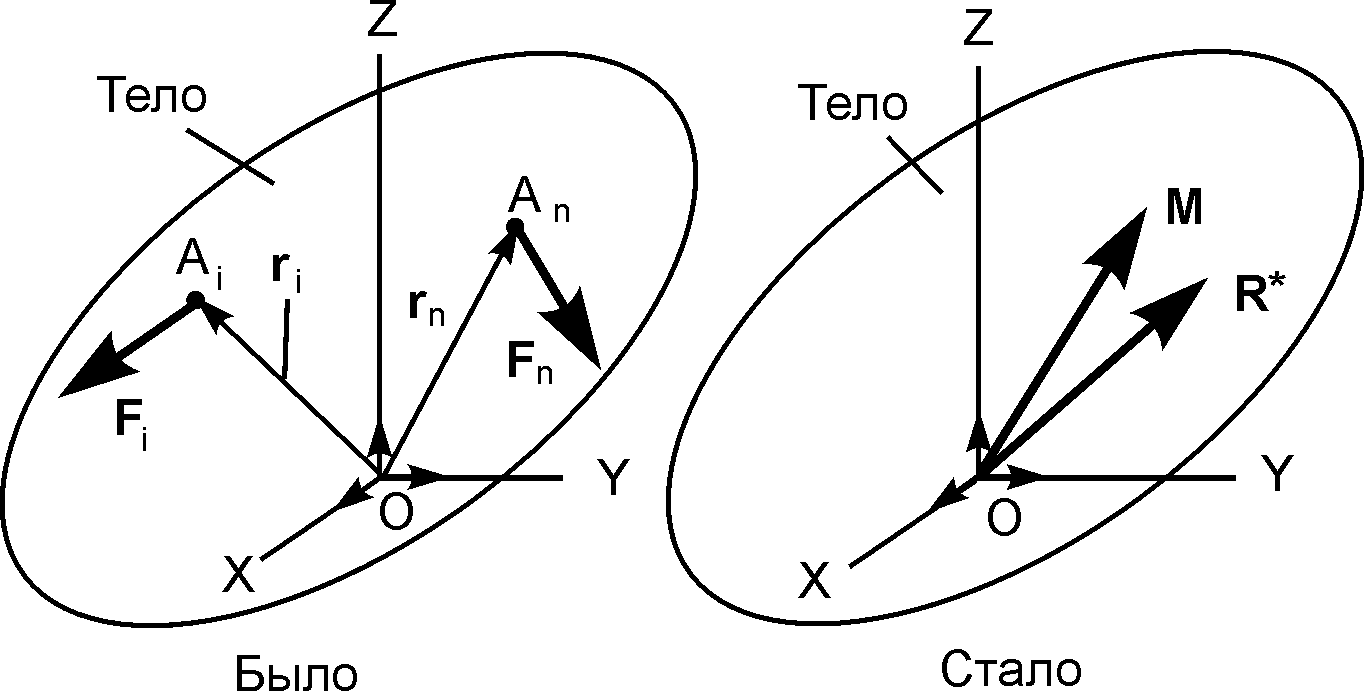Рис. 1.42

Пусть задана произвольная система сил (F₁, …, F_n) (рис. 1.42).

Последовательно применяя метод Пуансо к каждой из заданной системы сил, приведём её к произвольному центру О. В результате этого получим систему сил (F₁, …, F_n), приложенных в центре О, и присоединённую пару сил с моментом M = Σ M_О(F_i). Складывая силы F₁, …, F_n по правилу параллелограмма, получим их равнодействующую R^*, равную геометрической сумме заданных сил и приложенную в центре приведения.

Геометрическую сумму всех сил системы называют главным вектором системы сил и, в отличие от равнодействующей R, обозначают R^*.

Вектор M = Σ M_О(F_i) называют главным моментом системы сил относительно центра приведения.

Этот результат можно сформулировать следующим образом: силы, произвольно расположенные в пространстве, можно привести к одной силе, равной их главному вектору и приложенной в центре приведения и к паре сил с моментом, равным главному моменту всех сил относительно центра приведения.

Выбор центра приведения не отражается на модуле и направлении главного вектора R^*, но влияет на модуль и направление главного момента М. Главный вектор R^* является свободным вектором и может быть приложен в любой точке тела.

 

Аналитические условия равновесия

Плоской произвольной системы сил

 

 

Плоская произвольная система сил – система сил, линии действия которых произвольно расположены в одной плоскости.

 

Линии действия плоской произвольной системы сил пересекаются в различных точках.

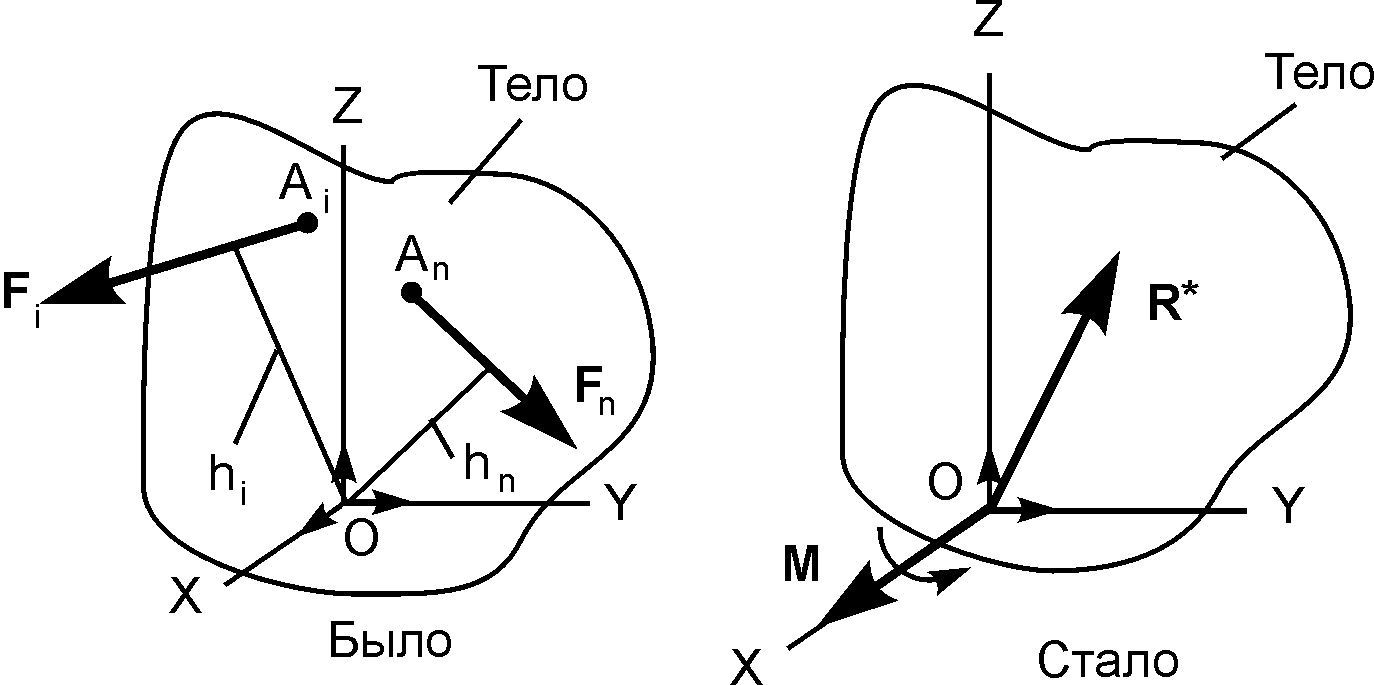Рис. 1.43

На рис. 1.43 изображена заданная плоская произвольная система сил (F₁, …, F_n), линии действия которых лежат в плоскости OYZ.

Последовательно применяя метод Пуансо для каждой из сил F_i, осуществим параллельный перенос сил из точек A_i в начало О системы отсчёта OXYZ. Согласно этому методу, сила F_iбудет эквивалентна силе F_i,приложенной в точке О, и присоединённой паре сил с моментом M_i = M_О(F_i). При этом M_i = ± F_i×h_i, где h_i – плечо силы F_i относительно центра приведения О. По окончании этой работы получим сходящуюся систему сил (F_i,…, F_n) и сходящуюся систему векторных моментов M_i = M_О(F_i) присоединённых пар сил, приложенных в центре приведения. Сложив векторы сил, получим глав

ный вектор R* = ΣF_i и главный момент эквивалентной пары сил          M = Σ M_О(F_i).

Таким образом, плоская произвольная система сил  (F_i,…, F_n) эквивалентна одной силе R* = Σ F_i и паре сил с моментом M = Σ M_О(F_i).

При решении задач статики используют проекции силы на координатные оси и алгебраические моменты сил относительно точки.

На рис. 1.44 изображена плоская произвольная система сил, приведённая к главному вектору сил, модуль которой               R*= 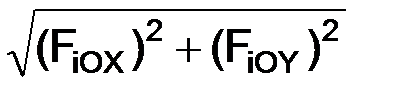 и эквивалентной паре сил с алгебраическим моментом M = Σ M_О(F_i).

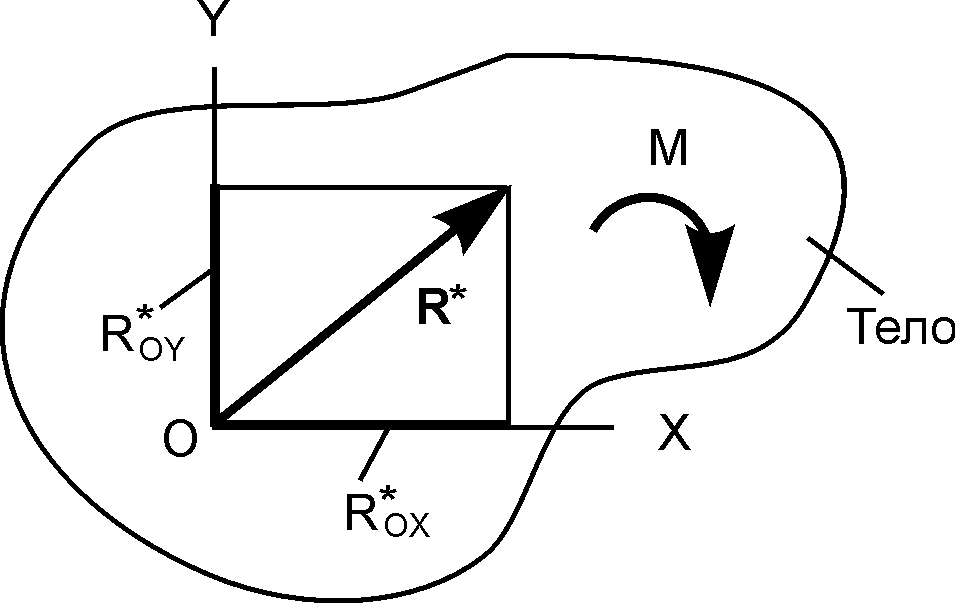Рис. 1.44

В этих формулах Σ F_iОX, Σ F_iОY – суммы проекций сил на координатные оси; Σ M_О(F_i) – сумма алгебраических моментов сил относительно точки О.

Геометрическое условие равновесия любой системы сил выражается векторными равенствами: R* = Σ F_i= 0; M = Σ M_О(F_i) = 0.

При решении задач требуется определить реакции R_i^E внешних связей, наложенных на механическую систему. При этом активные силы F_i^E, приложенные к этой системе, известны. Так как активные силы F_i^E и реакции связей R_i^E относятся к разряду внешних сил, то геометрическое условие равновесия системы внешних сил целесообразно выразить векторными равенствами:

 

Σ F_i^E + Σ R_i^E = 0;

Σ M_A(F_i^E) + Σ M_A(R_i^E) = 0.

 

Для равновесия системы внешних сил необходимо и достаточно, чтобы геометрическая сумма активных сил F_i^E и реакций R_i^E внешних связей и геометрическая сумма моментов активных сил M_A ( F_i^E) и реакций внешних связей M_A ( R_i^E ) относительно произвольной точки А равнялись нулю.

 

Проецируя эти векторные равенства на координатные оси системы отсчёта, получим аналитические условия равновесия системы внешних сил. Для плоской произвольной системы сил эти уравнения приобретают следующий вид:

Σ  + Σ  = 0;

Σ  + Σ  = 0;

Σ M_A(F_i^E) + Σ M_A(R_i^E) = 0,

где Σ ,Σ  – соответственно суммы проекций активных сил на координатные оси OX, OY; Σ ,Σ  – суммы проекций реакций внешних связей на координатные оси OX, OY; ΣM_A(F_i^E) – сумма алгебраических моментов активных сил F_i^E относительно точки А;   ΣM_A(R_i^E) – сумма алгебраических моментов реакций R_i^E внешних связей относительно точки А.

Совокупность этих формул есть первая (основная) форма уравнений равновесия плоской произвольной системы внешних сил.

Таким образом, для равновесия плоской произвольной системы внешних сил, приложенных к механической системе, необходимо и достаточно, чтобы суммы проекций активных сил и реакций внешних связей на две координатные оси и сумма алгебраических моментов активных сил и реакций внешних связей относительно произвольной точки А равнялись нулю.

 

Существуют и другие формы уравнений равновесия плоской произвольной системы сил.

Вторая форма выражается совокупностью формул:

Σ  + Σ  = 0;

Σ M_A(F_i^E) + Σ M_A(R_i^E) = 0;

Σ M_В(F_i^E) + Σ M_В(R_i^E) = 0.

Для равновесия плоской произвольной системы внешних сил, приложенных к телу, необходимо и достаточно, чтобы сумма проекций сил на координатную ось и суммы алгебраических моментов сил относительно произвольных точек А и В равнялись нулю.

Третья форма уравнений равновесия выражается совокупностью формул:

Σ M_A(F_i^E) + Σ M_A(R_i^E) = 0;

Σ M_В(F_i^E) + Σ M_В(R_i^E) = 0;

Σ M_С(F_i^E) + Σ M_С(R_i^E) = 0.

Для равновесия плоской произвольной системы внешних сил, приложенных к телу, необходимо и достаточно, чтобы суммы алгебраических моментов этих сил относительно произвольных точек А, В и С равнялись нулю.

 

При использовании третьей формы уравнений равновесия точки А, В и С не должны лежать на одной прямой.

 

 

---

Дата добавления: 2020-04-25; просмотров: 184; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!