Получите у преподавателя допуск для выполнения измерений.

МЕТОДИКА и ПОРЯДОК ИЗМЕРЕНИЙ

ЭКСПЕРИМЕНТ. Исследование диффузии частиц через тонкую трубку, соединяющую два объема.

Нажмите кнопку <СТАРТ> и через Dt секунд после начала процесса нажмите кнопки «½½» сверху во внешнем окне. Результат запишите в таблицу 2. Нажмите кнопку «uu». Через Dt секунд, нажав «½½», получите еще одну “мгновенную фотографию” и запишите количество частиц.

Закончив измерения с данной трубкой, установите второе значение диаметра соединительной трубки d₂из таблицы 1 и повторите измерения, записывая результат в таблицу 3, аналогичную таблице 2.

ТАБЛИЦА 1. Значения диаметров соединительной трубки, длительности промежутка измерения и сорта частиц.

Бригада	1	2	3	4	5	6	7	8
d₁, мм	10	12	14	16	10	12	14	16
d₂, мм	20	22	24	26	28	30	32	34
Dt , с	15	15	15	15	10	10	10	10
Сорт	красн	зелен	красн	зелен	красн	зелен	красн	зелен
Объем	справа	слева	справа	слева	справа	слева	справа	слева

ТАБЛИЦА 2

d₁=

t[с]=	Dt	2Dt	3Dt	4Dt	5Dt	6Dt	7Dt	8Dt	9Dt	10Dt
N(t)=

-

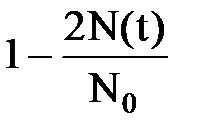
ТАБЛИЦА 3

d₂ =

t[с]=	Dt	2Dt	3Dt	4Dt	5Dt	6Dt	7Dt	8Dt	9Dt	10Dt
N(t)=

-

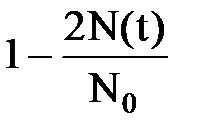
ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ

Вычислите и запишите в таблицы все указанные значения.

Постройте на одном рисунке графики экспериментальных зависимостей

- = f(t).

Используя формулу

D = ,

определите по графикам коэффициенты диффузии для каждого отверстия.

Длину отверстия L_отв измерьте линейкой на экране монитора, объем

сосуда V = 20 см³.

Найдите среднее значение коэффициента диффузии и, используя соотношение 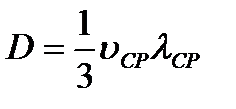, найдите среднюю скорость теплового движения υ_ср частиц (l_ср = 2 см).

Сделайте выводы по графику и ответу. В выводе по ответу сравните полученное экспериментально значение υ_срс величиной скорости, оцененной «на глаз».

РАСЧЕТЫ И ВЫВОДЫ:

Контрольные вопросы

1. Что происходит с макросистемой при нарушении равновесия?

2. Дайте определение явления переноса.

3. Назовите примеры явлений переноса.

4. Дайте определение явления диффузии.

5. Чем обусловлена диффузия?

6. В чем проявляется диффузия?

7. Какая диффузия называется одномерной?

8. Что такое самодиффузия?

9. Напишите уравнение одномерной диффузии для двухкомпонентной системы газов.

10. Каков физический смысл коэффициента диффузии.

11. Что такое плотность тела?

12. Что такое концентрация молекул (частиц)?

13. Дайте определение градиента плотности в общем случае.

14. Напишите формулу для градиента плотности, если она меняется только вдоль оси ОХ.

15. Напишите формулу для градиента плотности, если она меняется только вдоль оси ОY.

16. Напишите формулу для градиента плотности, если она меняется только вдоль оси ОZ.

17. Напишите формулу для градиента плотности, если она меняется вдоль осей ОХ и OY.

18. Что такое длина свободного пробега частицы?

19. Что такое эффективный диаметр и эффективное сечение частицы?

20. Какое уравнение связывает среднюю скорость с коэффициентом диффузии?

ЛАБОРАТОРНАЯ РАБОТА № 6

МАГНИТНОЕ ПОЛЕ

Цель работы: знакомство с моделированием магнитного поля от различных источников; экспериментальное подтверждение закономерностей для магнитного поля прямого провода и кругового витка (контура) с током; экспериментальное определение величины магнитной постоянной.

Данная лабораторная содержит описания, в которых используются компьютерные модели, разработанные фирмой «Физикон».

Для начала работы необходимо дважды щелкнуть левой кнопкой мыши, когда ее маркер расположен над эмблемой сборника компьютерных моделей. После этого появится начальная картинка, имеющая вид

После этого необходимо дважды щелкнуть левой кнопкой мыши, установив ее маркер над названием радела, в котором расположена данная модель

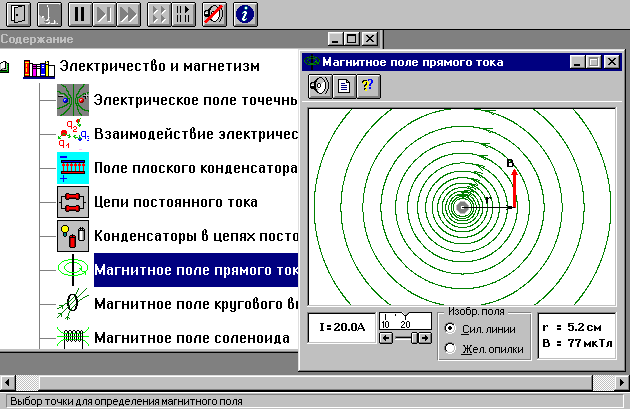
Запустите программу. Выберите «Электричество и магнетизм» и «Магнитное поле прямого тока».

КРАТКАЯ ТЕОРИЯ

Магнитным полем (МП) называется то, что существует в области пространства, в которой на электрически нейтральный проводник с током действует сила, называемая магнитной. Источником МП является движущаяся электрически заряженная частица (заряд), которая создает также и электрическое поле.

Если вблизи одной движущейся заряженной частицы (заряда №1) будет находиться вторая движущаяся с такой же скоростью υ заряженная частица (заряд №2), то на второй заряд будут действовать 2 силы: электрическая (кулоновская) и магнитная сила , которая будет меньше электрической в раз, где с – скорость света.

Для практически любых проводов с током выполняется принцип квазинейтральности: несмотря на наличие и движение заряженных частиц внутри проводника, любой (не слишком малый) его отрезок имеет нулевой суммарный электрический заряд. Поэтому между обычными проводами с током наблюдается только магнитное взаимодействие.

Магнитная индукция - характеристика силового действия МП на проводник с током, векторная величина, обозначаемая символом .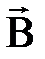

Линии магнитной индукции - линии, в любой точке которых вектор индукции МП направлен по касательной.

Анализ взаимодействия движущихся зарядов с учетом эффектов теории относительности (релятивизма) дает выражение для индукции МП, создаваемого элементарным отрезком 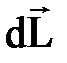c током I , расположенным в начале координат (закон Био-Савара-Лапласа или Б-С-Л):

где 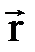- радиус-вектор точки наблюдения, - единичный радиус-вектор, направленный в точку наблюдения, m₀ - магнитная постоянная.

МП подчиняется принципу суперпозиции: индукция МП нескольких источников является суммой индукций полей, создаваемых независимо каждым источником .

Циркуляцией МП называется интеграл по некоторому контуру от скалярного произведения индукции МП на элемент контура: .

Закон циркуляции МП: циркуляция МП по замкнутому контуру L₀ пропорциональна суммарному току, пронизывающему поверхность S(L₀), ограниченную этим контуром L₀ . .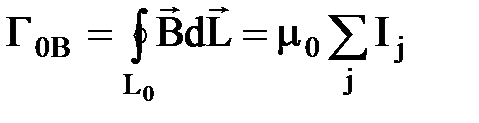

Закон Б-С-Л и принцип суперпозиции МП позволяют получить многие другие закономерности, в частности, индукцию магнитного поля прямого бесконечно длинного проводника с током: .

Линии магнитной индукции поля прямого проводника с током представляют собой концентрические окружности, лежащие в плоскостях, перпендикулярных проводнику, с центрами, расположенными на его оси.

Индукция МП на оси кругового контура (витка) радиуса R с током I на расстоянии r от центра: ,

где - магнитный момент витка площадью S, - единичный вектор нормали к поверхности витка.

Соленоидом называется длинная прямая катушка с током. Величина индукции МП вблизи центра соленоида меняется очень мало. Такое поле можно считать практически однородным.

Из закона циркуляции МП можно получить формулу для индукции МП в центре соленоида B = m₀In , где n – число витков, приходящихся на единицу длины соленоида.

МЕТОДИКА И ПОРЯДОК ИЗМЕРЕНИЙ

ТАБЛИЦА 1. Значения величин тока

Бригады	I₁	I₂	I₃	I₄
1 и 5	5	10	15	20
2 и 6	-5	-10	-15	-20
3 и 7	-15	-10	5	10
4 и 8	-20	-15	-10	5

Рассмотрите внимательно рисунок, изображающий компьютерную модель. Найдите на нем все основные регуляторы и поле эксперимента.

Дата добавления: 2020-04-08; просмотров: 200; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 4 567 Следующая ⇒

Мы поможем в написании ваших работ!