Оценка точности косвенных измерений
В случае косвенных измерений величина ‹X› определяется по результатам измерений других величин.
Пусть Хявляется некоторой функцией у и z, то есть:
Х= f(у; z). (9)
Тогда наилучшее значение при оценке ‹X› равно:
 (10)
(10)
где ‹у› и ‹z› ‑ находятся по формуле (4).
Абсолютная суммарная погрешность ∆X косвенных измерений находится через погрешности прямых измерений по правилу дифференцирования:
 . (11)
. (11)
Относительная погрешность δX косвенных измерений рассчитывается по формуле (8).
Для определения абсолютных и относительных погрешностей искомой величины при косвенных измерениях можно воспользоваться формулами дифференцирования в таблице 1.
| Таблица1. Формулы дифференцирования. | ||
| Функция | Абсолютная погрешность | Относительная погрешность |
| A = x +y | 
| 
|
| A = x - y | 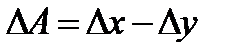
| 
|
| A = xyz | 
| 
|
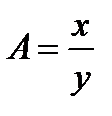
| 
| 
|

| 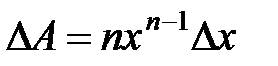
| 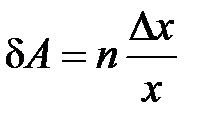
|
| A = xn + ym | 
| 
|

| 
| 
|

| 
| 
|
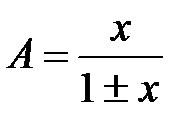
| 
| 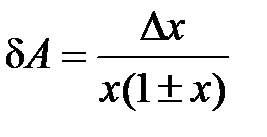
|

| 
| 
|
| 
| 
|

| 
| 
|

| 
| 
|

| 
| 
|

| 
| 
|
Правила предоставления результатов физического эксперимента
Точность экспериментально полученных физических величин ограничена точностью измерений. Например, при измерении длины тела с помощью обычной линейкой нельзя получить результат с точностью большой, чем ± 0.5 мм. В то же время, вычисляя значения ‹X› по формуле (4) и ∆Х по формуле (5) и (6), можно точно получить числа с несколькими десятичными знаками, соответствующие микронам и даже их долям. Очевидно, что эти десятичные знаки не отражают реальной точности измерений и, следовательно, при представлении результатов в виде Х=‹X›±∆Х численные значения величин ‹X› и ∆Х должны быть предварительно обработаны.
1. Погрешность ∆Х округляется и записывается только с одной значащей цифрой.
Например: результат вычислений 0.0263 записывается в виде ∆Х = 0.03;
321 в виде ∆Х = 300.
2. Среднеарифметическое значение ‹X› округляется так, что значащие цифры остаются только в тех разрядах, которые не младше значащей цифры погрешности ∆Х.
Например: результат вычислений 7714161.8434 при ∆Х=0.03 округляется до ‹X›= 7714161.84, а при ∆Х=300 до ‹X›=7714200.
Окончательно экспериментально измеренная физическая величина представляется в виде Х=7714161.84 ± 0.03 при ∆Х=0.03
и в виде Х=7714200 ± 300 при ∆Х=300.
ВЫПОЛНЕНИЯ РАБОТЫ
Задание : измерение объема тела (цилиндра).
1. Штангенциркулем измерить высоту цилиндра h, микрометром – диаметр цилиндра d. Замеры выполнить 5 раза и данные занести в таблицу 2.
2. По формуле (4) найти среднеарифметические значения размеров тела ‹h› и ‹d›.
3. По формуле (5) найти случайные составляющие погрешностей измерений ∆hсл и ∆dсл.
4. Найти систематические погрешности измерений ∆hпр и ∆dпр (погрешности инструмента).
5. Рассчитать абсолютные суммарные погрешности измерений ∆h и ∆d по формуле (6).
6. Результаты всех расчетов занести в таблицу 2.
Таблица 2.
| № | h, м | d, м | ∆hсл, м | ∆dсл, м | ∆hпр, м | ∆dпр,м | ∆h, м | ∆d, м | ‹V›,м3 | ∆V,м3 | δ V,% |
| 1 |
|
|
|
|
|
|
|
|
| ||
| 2 | |||||||||||
| 3 | |||||||||||
| 4 | |||||||||||
| 5 | |||||||||||
| Ср. |
7. Вычислить среднее значение объема ‹V› цилиндра по формуле:

8. Определить абсолютную погрешность ∆V косвенных измерений объема тела:

9. По формуле (8) найти относительную погрешность измерений δ V.
10. Результаты вычислений объема тела записать в виде:
V = (‹V› ± ∆V) м3.
РАСЧЕТЫ И ВЫВОДЫ:
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что такое измерение? Назовите виды измерений.
2. Какие бывают погрешности и за счет чего они возникают?
3. Что указывает класс точности прибора? Назовите классы точности приборов.
4. Как определить суммарную погрешность прямых измерений?
5. Как определить погрешность косвенных измерений?
6. Что такое относительная погрешность?
7. Как устроены штангенциркуль и микрометр. Как пользоваться этими приборами?
8. Правила округления результатов физического эксперимента.
9. В каком виде следует представлять результаты измерений физических величин?
ЛАБОРАТОРНАЯ РАБОТА № 2
МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
Цель работы: выбор физических моделей для анализа движения тел;исследование движения тела под действием квазиупругой силы;экспериментальное определение зависимости частоты колебаний от параметров системы.
Данная лабораторная содержит описания, в которых используются компьютерные модели, разработанные фирмой «Физикон».
Для начала работы необходимо дважды щелкнуть левой кнопкой мыши, когда ее маркер расположен над эмблемой сборника компьютерных моделей. После этого появится начальная картинка, имеющая вид

После этого необходимо дважды щелкнуть левой кнопкой мыши, установив ее маркер над названием радела, в котором расположена данная модель.
Выберите «Механические колебания и волны» и «Свободные колебания» (сначала математический маятник, потом груз на пружине). Нажмите вверху внутреннего окна кнопку с изображением страницы.
КРАТКАЯ ТЕОРИЯ
Колебание - периодически повторяющееся движения тела.
Период T - минимальное время, через которое движение полностью повторяется.
Гармоническое колебание - движение, при котором координата тела меняется со временем по закону синуса или косинуса:
 .
.
Дата добавления: 2020-04-08; просмотров: 171; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
