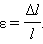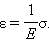ОБРАБОТКА РЕЗУЛЬТАТОВ И ОФОРМЛЕНИЕ ОТЧЕТА
Вычислите требуемые величины и заполните таблицы 2 и 3.
Постройте графики зависимости:
· квадрата периода колебаний от длины нити ММ,
· квадрата циклической частоты колебаний от жесткости пружины ПМ.
По наклону графика Т2 = f(L) определите значение g, используя формулу
g =.4 p 2 
.
Оцените абсолютную ошибку определения g.
По наклону графика w 2 = f( k ) определите значение m , используя формулу
m =. 
.
Оцените абсолютную ошибку определения m.
Проанализируйте ответ и графики.
РАСЧЕТЫ И ВЫВОДЫ:
Контрольные вопросы
1. Что такое колебание?
2. Дайте определение периода колебаний.
3. Дайте определение частоты колебаний.
4. Дайте определение гармонических колебаний.
5. Запишите закон зависимости от времени характеристики А, совершающей гармоническое колебательное изменение.
6. Запишите закон движения МТ, совершающей гармонические колебания.
7. Дайте определение амплитуды гармонических колебаний.
8. Дайте определение фазы гармонических колебаний.
9. Дайте определение начальной фазы гармонических колебаний.
10. Напишите уравнение связи частоты и периода гармонических колебаний.
11. Напишите уравнение связи частоты и циклической частоты гармонических колебаний.
12. Напишите формулу зависимости скорости МТ от времени при гармонических колебаниях.
|
|
|
13. Напишите уравнения связи амплитуды скорости и амплитуды смещения при гармонических колебаниях МТ.
14. Напишите формулу зависимости ускорения МТ от времени при гармонических колебаниях.
15. Напишите уравнения связи амплитуды скорости и амплитуды ускорения при гармонических колебаниях МТ.
16. Напишите уравнения связи амплитуды смещения и амплитуды ускорения при гармонических колебаниях МТ.
17. Напишите дифференциальное уравнение свободных гармонических колебаний МТ.
18. Напишите дифференциальное уравнение свободных затухающих колебаний МТ.
19. Что определяет коэффициент затухания?
20. Дайте определение математического маятника.
21. Запишите формулу циклической частоты свободных колебаний математического маятника.
22. Дайте определение пружинного маятника.
23. Запишите формулу циклической частоты свободных колебаний пружинного маятника.
24. Какие процессы происходят при вынужденных колебаниях?
25. Что такое резонанс?
26. При каком затухании резонанс будет более резким?
Лабораторная работа № 3
ОПРЕДЕЛЕНИЕ МОДУЛЯ УПРУГОСТИ ТВЁРДЫХ ТЕЛ
Цель работы : научиться определять модули упругости твёрдых тел.
Приборы и оборудование: установка для изучения упругих свойств материалов; набор грузиков; микрометр; штангенциркуль; линейка; образцы упругих материалов.
|
|
|
КРАТКАЯ ТЕОРИЯ
По своим физическим свойствам и молекулярной структуре твердые тела разделяются на два класса – аморфные и кристаллические тела.
Характерной особенностью аморфных тел является их изотропность, т. е. независимость всех физических свойств (механических, оптических и т. д.) от направления. Молекулы и атомы в изотропных твердых телах располагаются хаотично, образуя лишь небольшие локальные группы, содержащие несколько частиц (ближний порядок). По своей структуре аморфные тела очень близки к жидкостям. Примерами аморфных тел могут служить стекло, различные затвердевшие смолы (янтарь), пластики и т. д. Если аморфное тело нагревать, то оно постепенно размягчается, и переход в жидкое состояние занимает значительный интервал температур.
В кристаллических телах частицы располагаются в строгом порядке, образуя пространственные периодически повторяющиеся структуры во всем объеме тела. Для наглядного представления таких структур используются пространственные кристаллические решетки, в узлах которых располагаются центры атомов или молекул данного вещества. Чаще всего кристаллическая решетка строится из ионов (положительно и отрицательно заряженных) атомов, которые входят в состав молекулы данного вещества. Например, решетка поваренной соли содержит ионы Na+ и Cl–, не объединенные попарно в молекулы NaCl (рис. 1). Такие кристаллы называются ионными.
|
|
|
|
| Рис. 1. Кристаллическая решетка поваренной соли. |
В каждой пространственной решетке можно выделить структурный элемент минимального размера, который называется элементарной ячейкой. Вся кристаллическая решетка может быть построена путем параллельного переноса (трансляции) элементарной ячейки по некоторым направлениям.
Теоретически доказано, что всего может существовать 230 различных пространственных кристаллических структур. Большинство из них (но не все) обнаружены в природе или созданы искусственно.
Кристаллические решетки металлов часто имеют форму шестигранной призмы (цинк, магний), гранецентрированного куба (медь, золото) или объемно центрированного куба (железо).
Кристаллические тела могут быть монокристаллами и поликристаллами. Поликристаллические тела состоят из многих сросшихся между собой хаотически ориентированных маленьких кристалликов, которые называются кристаллитами. Большие монокристаллы редко встречаются в природе и технике. Чаще всего кристаллические твердые тела, в том числе и те, которые получаются искусственно, являются поликристаллами.
|
|
|
В отличие от монокристаллов, поликристаллические тела изотропны, т. е. их свойства одинаковы во всех направлениях. Поликристаллическое строение твердого тела можно обнаружить с помощью микроскопа, а иногда оно видно и невооруженным глазом (чугун).
Многие вещества могут существовать в нескольких кристаллических модификациях (фазах), отличающихся физическими свойствами. Это явление называется полиморфизмом. Переход из одной модификации в другую называется полиморфным переходом. Интересным и важным примером полиморфного перехода является превращение графита в алмаз. Этот переход при производстве искусственных алмазов осуществляется при давлениях 60–100 тысяч атмосфер и температурах 1500–2000 К.
Структуры кристаллических решеток экспериментально изучаются с помощью дифракции рентгеновского излучения на монокристаллах или поликристаллических образцах.
На рис. 2 приведены примеры простых кристаллических решеток. Следует помнить, что частицы в кристаллах плотно упакованы, так что расстояние между их центрами приблизительно равно размеру частиц. В изображении кристаллических решеток указывается только положение центров частиц.
В простой кубической решетке частицы располагаются в вершинах куба. В гранецентрированной решетке частицы располагаются не только в вершинах куба, но и в центрах каждой его грани. Изображенная на рис. 1. решетка поваренной соли состоит из двух вложенных друг в друга гранецентрированных решеток, состоящих из Na+ и Cl– . В объемноцентрированной кубической решетке дополнительная частица располагается в центре каждой элементарной кубической ячейки.
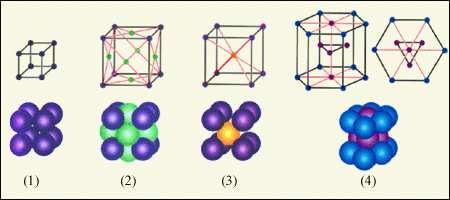Рис.2. Простые кристаллические решетки: 1 – простая кубическая решетка; 2 – гранецентрированная кубическая решетка; 3 – объемноцентрированная кубическая решетка; 4 – гексагональная решетка.
|
Кристаллические структуры металлов имеют важную особенность. Положительно заряженные ионы металла, образующие кристаллическую решетку, удерживаются вблизи положений равновесия силами взаимодействия с «газом свободных электронов» (рис. 3.). Электронный газ образуется за счет одного или нескольких электронов, отданных каждым атомом. Свободные электроны способны блуждать по всему объему кристалла.
|
| Рис. 3. Структура металлического кристалла. |
В твердых телах – аморфных и кристаллических – частицы (молекулы, атомы, ионы) совершают тепловые колебания около положений равновесия, в которых энергия их взаимодействия минимальна. При увеличении расстояния между частицами возникают силы притяжения, а при уменьшении – силы отталкивания. Силы взаимодействия между частицами обусловливают механические свойства твердых тел.
Деформация твердого тела является результатом изменения под действием внешних сил взаимного расположения частиц, из которых состоит тело, и расстояний между ними.
Существует несколько видов деформаций твердых тел. Некоторые из них представлены на рис. 4.
|
| Рис. 4. Некоторые виды деформаций твердых тел: 1 – деформация растяжения; 2 – деформация сдвига; 3 – деформация всестороннего сжатия. |
В твердых телах деформация называется упругой, когда после прекращения действия сил деформация полностью исчезает, и пластической (остаточной), когда после прекращения действия сил деформация не исчезает; если она исчезает не полностью, то деформация называется упругопластической. Принято различать следующие виды деформации: растяжение, сжатие, сдвиг, кручение, изгиб.
Простейшим видом деформации является деформация растяжения или сжатия. Ее можно характеризовать абсолютным удлинением Δl, возникающим под действием внешней силы 
Связь между Δl и F зависит не только от механических свойств вещества, но и от геометрических размеров тела (его толщины и длины).
Отношение абсолютного удлинения Δl к первоначальной длине l образца называется относительным удлинением или относительной деформацией ε:
|
При растяжении ε > 0, при сжатии ε < 0.
Если принять направление внешней силы, стремящейся удлинить образец, за положительное, то F > 0 при деформации растяжения и F < 0 – при сжатии. Отношение модуля внешней силы F к площади S сечения тела называется механическим напряжением σ:
|
За единицу механического напряжения в СИ принят паскаль (Па). Механическое напряжение измеряется в единицах давления.
Зависимость между ε и σ является одной из важнейших характеристик механических свойств твердых тел. Графическое изображение этой зависимости называется диаграммой растяжения. По оси абсцисс откладывается относительное удлинение ε, а по оси ординат – механическое напряжение σ. Типичный пример диаграммы растяжения для металлов (таких как медь или мягкое железо) представлен на рис. 5.
|
| Рис. 5. Типичная диаграмма растяжения для пластичного материала. |
При малых деформациях (обычно существенно меньших 1 %) связь между σ и ε оказывается линейной (участок Oa на диаграмме). При этом при снятии напряжения деформация исчезает. Такая деформация называется упругой. Максимальное значение σ = σпр, при котором сохраняется линейная связь между σ и ε, называется пределом пропорциональности (точка a).
На линейном участке выполняется закон Гука:
|
Коэффициент E в этом соотношении называется модулем Юнга.
При дальнейшем увеличении напряжения связь между σ и ε становится нелинейной (участок ab). Однако при снятии напряжения деформация практически полностью исчезает, т. е. восстанавливаются размеры тела. Максимальное напряжение на этом участке называется пределом упругости.
Если σ > σупр , образец после снятия напряжения уже не восстанавливает свои первоначальные размеры и у тела сохраняется остаточная деформация εост . Такие деформации называются пластическими (участки bc, cd и de). На участке bc деформация происходит почти без увеличения напряжения. Это явление называется текучестью материала. В точке d достигается наибольшее напряжение σmax , которое способен выдержать материал без разрушения (предел прочности). В точке e происходит разрушение материала.
Материалы, у которых диаграмма растяжения имеет вид, показанный на рис. 5., называются пластичными. У таких материалов обычно деформация εmax , при которой происходит разрушение, в десятки раз превосходит ширину области упругих деформаций. К таким материалам относятся многие металлы.
Материалы, у которых разрушение происходит при деформациях, лишь незначительно превышающих область упругих деформаций, называются хрупкими (стекло, фарфор, чугун).
Аналогичным закономерностям подчиняется и деформация сдвига (рис. 4 .2.). В этом случае вектор силы 
направлен по касательной к поверхности образца. Относительная деформация определяется безразмерным отношением Δx / l, а напряжение – отношением F / S (сила, действующая на единицу площади поверхности). При малых деформациях
|
Коэффициент пропорциональности G в этом отношении называется модулем сдвига. Модуль сдвига для большинства твердых материалов в 2–3 раза меньше модуля Юнга. Например, у меди E = 1,1·1011 Н/м2, G = 0,42·1011 Н/м2. Следует помнить, что у жидких и газообразных веществ модуль сдвига равен нулю.
На рис. 4.3. показана деформация всестороннего сжатия твердого тела, погруженного в жидкость. В этом случае механическое напряжение совпадает с давлением p в жидкости. Относительная деформация определяется как отношение изменения объема ΔV к первоначальному объему V тела. При малых деформациях
|
Коэффициент пропорциональности B в этой формуле называется модулем всестороннего сжатия.
Всестороннему сжатию могут подвергаться не только твердые тела, но и жидкости и газы. У воды B = 2,2·109 Н/м2, у стали B = 1,6·1011 Н/м2. На дне Тихого океана, на глубине порядка 4 км, давление p приблизительно равно 4·107 Н/м2. В этих условиях относительное изменение ΔV / V объема воды составляет 1,8 %, в то время как для стального тела оно составляет всего лишь 0,025 %, т. е. в 70 раз меньше. Твердые тела с их жесткой кристаллической решеткой значительно менее сжимаемы по сравнению с жидкостями, атомы и молекулы которых не так сильно связаны со своими соседями. Сжимаемость газов на много порядков выше, чем у жидкостей и твердых тел.
Величина модуля всестороннего сжатия определяет скорость звука в данном веществе.
МЕТОДИКА ИЗМЕРЕНИЙ
Значение модуля упругости удобно определять по изгибу образца. Образец размещают на опорах (рис.6). Затем к середине образца подвешивают груз p. В этом случае нижняя часть образца испытывает деформацию - растяжения, а верхняя - деформацию сжатия. При этом середина образца испытывает перемещение λ, называемое стрелой прогиба (рис.7).
| Рис. 6 |
| l |
| a |
| Рис. 7 |
В теории сопротивления материалов показывается, что для образцов в виде пластины модуль упругости определяется следующей формулой:
, (1)
где Ε – модуль упругости (Па);
Ρ – ( Ρ = m·g) вес нагрузки (Н);
l – длина образца (между опорами) (м);
λ – стрела прогиба (м);
b – ширина образца (м);
a – толщина образца (м).
Для измерения модуля упругости применяется экспериментальная установка, изображенная на рис. 8.
Экспериментальный образец помещают на неподвижные стойки. Расстояние между стойками принимается равным длине образца. Подводят стержень микрометра до соприкосновения с образцом - показание n1; делаем нагрузку на стержень и подводим стержень микрометра вновь до соприкосновения с образцом – показание n2 , определяют стрелу прогиба по формуле: λ = n2 –n1 .
| О |
| С |
| С |
| Г |
| М |
| λ |
| Рис. 8 |
М - микрометр для измерения стрелы изгиба;
О - образец;
С - стойки;
Г - грузики.
ВЫПОЛНЕНИЕ РАБОТЫ
1. Штангенциркулем измерьте ширину, толщину и длину образца. Каждое измерение делайте пять раз в разных местах и значения запишите в таблицу.
2. Подведите стержень микрометра к образцу. Снимите показания микрометра n1.
3. Последовательно нагружая образец грузами, подводите стержень микрометра к образцу и, измеряя положение образца n2, вычисляйте стрелу прогиба λ.
4. Вычисляйте модуль упругости для каждого образца по формуле (1).
5. Опыт повторите не менее 5 раз
6. Рассчитайте абсолютную погрешность ΔЕ.
| № | l, м | b, м | а , м | P, H | λ, м | Е, Па | ΔЕ, Па |
| 1 | |||||||
| 2 | |||||||
| 3 | |||||||
| 4 | |||||||
| 5 | |||||||
| ср |
РАСЧЕТЫ И ВЫВОДЫ:
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какие виды твердых тел существуют?
2. Что такое изотропность?
3. Приведите примеры аморфных тел.
4. Что такое кристаллическая решетка?
5. Что такое элементарная ячейка?
6. Что такое монокристаллы и поликристаллы?
7. Что такое полиморфизм?
8. Перечислите основные виды кристаллических решеток.
9. Что называется деформацией?
10. Какие существуют виды и типы деформации?
11. Что такое относительное удлинение?
12. Что такое механическое напряжение?
13. Изобразите диаграмму растяжения твердого тела.
14. Сформулируйте закон Гука.
15. Что такое предел пропорциональности?
16. Что такое предел упругости?
17. Что такое текучесть материала?
18. Что такое предел прочности?
19. Чем отличается упругая деформация от пластической (остаточной)?
20. Чем отличаются пластичные материалы от хрупких?
21. Что такое модуль сдвига и модуль всестороннего сжатия?
22. Что определяет скорость звука в веществе?
ЛАБОРАТОРНАЯ РАБОТА № 4
Дата добавления: 2020-04-08; просмотров: 392; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!