МЕТОДЫ ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТА ВЯЗКОСТИ ЖИДКОСТИ

⇐ ПредыдущаяСтр 5 из 7Следующая ⇒

Цель работы : 1. Изучить различные методы определения вязкости жидкостей. 2. Научиться определять коэффициент вязкости жидкостей методом Стокса.

Приборы и оборудование : цилиндр мерный прозрачный; исследуемая жидкость; секундомер; масштабная линейка; вискозиметр Освальда (типа ВПЖ–2); вискозиметр крови (типа ВК-4).

КРАТКАЯ ТЕОРИЯ

Определение вязкости широко используется в технике, агрономии, биологии, ветеринарии и т.д. Например, в технике коэффициент вязкости используется для определения качества горюче-смазочных материалов, его приходится учитывать при определении энергии, необходимой для перекачки жидкостей по трубам и подачи воздуха при создании микроклимата для животных и растений; в агрономии – для определения структуры почв; в ветеринарии – вязкость крови учитывается при диагностике состояния животного.

Все реальные жидкости и газы обладают вязкостью.

Вязкость веществ или внутреннее трение – это свойство жидкости или газа, благодаря которому выравниваются скорости движения различных слоев. Это выравнивание может быть частичным или полным. Другими словами, под вязкостью понимают способность жидкости или газа создавать сопротивление перемещению одного слоя вещества относительно другого. Это происходит за счет действия межмолекулярных сил. Из слоя жидкости с большей скоростью за счет теплового беспорядочного движения молекул переносится количество движения (импульс молекул) к слою, движущемуся с меньшей скоростью, и наоборот. При этом слои «быстрые» тормозятся, а слои «более медленные» начинают двигаться с большей скоростью. Так возникает между слоями жидкости сила внутреннего трения.

Количественно силу внутреннего трения, возникающую при переносе количества движения между слоями жидкости, движущимися с различными скоростями, можно определить следующим образом. Рассмотрим жидкость, которая движется в направлении оси Х. Пусть один слой движется со скоростью υ, а другой со скоростью (υ + ∆ υ). Расстояние между двумя точками выбранных слоев, для которых скорости отличаются на ∆ υ, равно ∆Z (рис.1).

υ + ∆ υ

ΔZ

Рис.1

Отношение характеризует изменение скорости потока в направлении оси Z (в направлении перпендикулярном вектору скорости).

Как было показано Ньютоном, сила вязкости, действующая между двумя слоями, выражается формулой:

или , (1)

где η – коэффициент пропорциональности, называемый коэффициентом внутреннего трения или коэффициентом динамической вязкости; S - площадь соприкосновения слоёв.

Знак «±» показывает, что сила вязкости действует по направлению движения на «медленный » слой и противоположно движению на «быстрый» слой.

Коэффициент динамической вязкости численно равен силе внутреннего трения, возникающей на каждой единице поверхности соприкосновения двух слоев, движущихся с разными скоростями. При этом отношение разности скоростей к расстоянию между этими плоскостями равно единице. Единица измерения коэффициента вязкости η в СИ: Па·с (Паскаль · секунда).

В биологической и сельскохозяйственной литературе встречается ранее применявшаяся единица вязкости пуаз (П): 10П = 1 Па∙с.

Коэффициент динамической вязкости веществ зависит от природы вещества и от температуры (с повышением температуры вязкость жидкости уменьшается, а вязкость газа увеличивается).

Вязкость играет существенную роль при движении твёрдых тел в жидкостях. Если внутри жидкости будет перемещаться твердое тело, то о его поверхность будут ударяться молекулы жидкости, и в итоге будет возникать трение, как между двумя слоями жидкости.

На тело, движущееся внутри жидкости или газа, действует сила внутреннего трения:

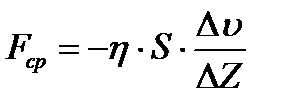(1а)

где знак «-» - означает, что сила внутреннего трения направлена против движения тела, ∆υ - разность между скоростью жидкости прилипшей к телу (скорость тела) и скоростью любого другого слоя (например, прилипшего к берегу υ=0), S – общая площадь соприкосновения тела со средой.

Помещая слои жидкости между двумя трущимися поверхностями твердых тел, можно заменить трение скольжения внутренним трением, а последнее, как известно, значительно меньше.

Вязкость биологических растворов (крови, ее плазмы, сыворотки и др.) - важный показатель функционального состояния цитоплазмы клеток. Вязкость жидкости играет значительную роль в диагностике различных заболеваний. При некоторых инфекционных заболеваниях вязкость крови увеличивается, а при туберкулезе, брюшном тифе - уменьшается. Венозная кровь обладает большей вязкостью, чем артериальная. При тяжелой физической работе вязкость крови увеличивается.

По вязкости судят о качестве некоторых продуктов питания, например, сахара, сиропа, соков, сгущенного молока и т.д.

Определять вязкость при помощи закона Ньютона (формула 1) сложно. Но существует около 20 других способов определения вязкости.

Совокупность методов измерения вязкости называется вискозиметрией, а приборы, применяемые для этих целей, называются вискозиметрами (от лат. viscous – клейкий).

Рассмотрим три основных метода определения вязкости: капиллярный,метод Стокса и ротационный.

Капиллярный метод

Этим методом измеряют вязкость в пределах от 10^-5 Па∙с (свойственно газам) и до 10⁴ Па∙с (свойственно консистентным смазкам).

Объем жидкости ∆V, протекающей за время ∆t, через трубу сечением S, выражается формулой:

ΔV = S υ Δt, (2)

а если труба круглая, то

ΔV = πr² υ Δt, (3)

где r – радиус трубы, υ– скорость ламинарного течения.

Поток жидкости через сечение трубы определяется формулой:

Используя (2) и (3), можно записать

Q = S· υ = π r² υ (4)

для трубы круглого сечения.

Скорость ламинарного течения по круглой трубе определяется законом Пуазейля:

, (5)

где ∆P – разность давлений на участке трубки длиной ℓ=∆х, η – коэффициент динамической вязкости жидкости или газа.

Откуда поток равен

. (6)

Oбъем протекающей жидкости

(7)

или получаем формулу Пуазейля

(8)

на которой основан капиллярный метод, где V – объем жидкости, протекающей через капилляр (м³), t – время протекания жидкости (с), ℓ =Δx - длина капилляра (м), r – радиус капилляра (м), η – динамическая вязкость жидкости (Па∙с), ∆Р – разность давлений на концах трубки (Па).

Капиллярный метод заключается в измерении времени протекания жидкости через капилляр под действием силы тяжести при определенном перепаде давлений. При определении вязкости капиллярным методом необходимо добиваться, чтобы течение жидкости было ламинарным, т.к. при турбулентном движении формула Пуазейля несправедлива. Ламинарным (лат. lamina – пластинка) называется такое течение вязкой жидкости, при котором отсутствует перемешивание между соседними слоями потока. При увеличении скорости движения жидкости из-за неоднородностей давления по поперечному сечению трубы создаются завихрения и движение становиться турбулентным (лат. turbulentus–неспокойным).

Характер течения жидкости можно определить кинематической вязкостью, которая с динамической вязкостью связана соотношением

, (9) где ν – кинематическая вязкость (м²/с); η – динамическая вязкость (Па∙с); ρ – плотность жидкости (кг/м³).

Ранее применялась и нередко встречается в литературе единица вязкости стокс: 1м²/с = 104 Стокс.

Величина, обратная динамической вязкости, φ = 1/η называется текучестью.

Жидкости в капилляре движутся под действием гидростатического давления

(10)

где ρ – плотность жидкости (кг/м²); g – ускорение свободного падения (м/с²); h – разность уровней жидкости в коленах вискозиметра (м).

Применим закон Пуазейля (2) для воды: .

И для исследуемой жидкости: .

Если объёмы двух вытекающих жидкостей будут одинаковые, то, приравнивая правые части этих уравнений и сокращая, получим:

и т.к. , то

или после сокращения

Переходя к кинематической вязкости, получим: .

Величина называется постоянной прибора, и тогда расчетная формула для капиллярного метода примет вид:

, (11)

где σ = 12,8 ∙ 10^-6 м²/с.

Капиллярный метод определения вязкости применяется для определения вязкости крови. Для этих целей применяется специальный гемовискозиметр типа ВК-4 (греч. haima – кровь).

Принцип его действия основан на том, что скорости продвижения жидкостей в капиллярах одинакового сечения при одних и тех же температуре и давлении зависят от вязкостей жидкостей.

По формуле Пуазейля для разных жидкостей

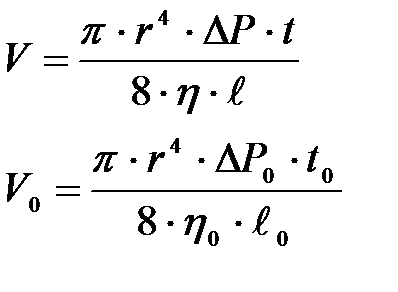
Разделив одно уравнение на другое, получим при t = t₀

где η – динамическая вязкость исследуемой жидкости; η₀ – динамическая вязкость воды; для цилиндрических объёмов

V = S ℓ, V₀ = S ℓ_о

и если сечения одинаковые, то

(12)

– расчетная формула для определения вязкости гемовискозиметром при известном коэффициенте вязкости эталонной жидкости.

Измерение вязкости при помощи капиллярного вискозиметра основано на определении времени истечения через капилляр определенного объема жидкости из измерительного резервуара.

Метод Стокса

Этот метод основан на определении времени падения шарика в жидкости. С помощью метода Стокса определяют вязкость в пределах от 6∙10^-4 Па∙с до 250 Па∙с.

На движущиеся в жидкости тело шарообразной формы действует сила внутреннего трения, тормозящая его движение. Для малых скоростей Стокс показал, что эта сила вязкости пропорциональна линейным размерам шарика и скорости его движения:

, (13)

где d – диаметр шарика, υ - скорость движения шарика.

Закон Стокса справедлив для движения тел шарообразной формы не только в жидкостях, но и газах. В частности, с помощью закона Стокса можно вычислить время оседания пыли в воздухе. (На основе этого расчета получается, что для выпадения пыли в комнате высотой 3м, при полной неподвижности воздуха требуется около 12 суток.)

Применяется закон Стокса и в технологии молочных продуктов. Например, с помощью его, принимая, что молочный жир имеет форму шарика, можно определить время отстаивания сливок от молока. Вязкость молока лежит в основе расчетов при конструировании выпарных аппаратов, подборе технологического оборудования для производства плавленых сыров, конструкции сепараторов, молокопроводов, характеризует консистенцию молочных продуктов.

Если шарик вертикально падает в жидкости, то на него, кроме силы вязкости F, действует сила тяжести Р и выталкивающая сила F_A (сила Архимеда) ( рис.2.).

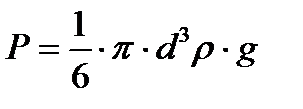Сила тяжести Р = mg, масса тела m = ρV; т.к. объем шарика , то вес шарика Р равен: . (14)

На основании закона Архимеда выталкивающая сила равна весу жидкости, вытесненной шариком:

(15)

Объем вытесненной жидкости равен объему шарика. Тогда:

(16)

В начале шарик двигается с ускорением, при этом сила вязкости меняется. Затем наступает момент, когда скорость шарика достигает такого значения, при котором векторная сумма всех сил равна нулю, т.е. выполняется первый закон Ньютона, и дальнейшее падение шарик совершает с постоянной скоростью. Запишем равенство:

(17)

Из равенства следует:

Скорость равномерно движущегося шарика:

, где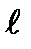

- путь, пройденный шариком за время t.

Рис. 2.

Окончательная расчетная формула для коэффициента вязкости методом Стокса:

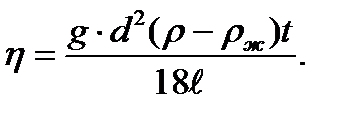(18)

Прибор для определения коэффициента вязкости методом Стокса состоит из стеклянного цилиндра, наполненного исследуемой жидкостью (рис.5). Вверху цилиндр прикрыт крышкой с отверстием посредине для опускания шарика. На поверхности цилиндра имеются две метки (А и В), расположенные друг от друга на расстоянии ℓ. Метки выполнены в виде колец из тонкой проволоки или резины. Верхняя метка опущена ниже уровня жидкости на 8-10 см. На этом участке в 8-10 см шарик достигает постоянной скорости.

Рис.5

Ротационный метод

Этот метод используется для измерения вязкости в пределах от 1 Па∙с до 10⁵Па∙с, т.е. смазочных масел, расплавленных силикатов и металлов, высоковязких лаков и клеев, глинистых растворов и т.п.

Сущность ротационного метода заключается в следующем: жидкость заливается между двумя соосными телами (цилиндрами). Один из цилиндров (ротор) вращается, другой неподвижен. Вязкость измеряется или по угловой скорости ротора при постоянной мощности двигателя, создающего определенный момент силы на неподвижном цилиндре, или по моменту силы, действующему на неподвижный цилиндр при заданной угловой скорости вращения ротора.

Возможно также измерение вязкости через определение скорости вращения цилиндра, опущенного в вязкую среду при фиксированных параметрах цилиндра и постоянном напряжении на электродвигателе.

ВЫПОЛНЕНИЕ РАБОТЫ

(определение вязкости методом Стокса)

1. Измерить микрометром диаметр самого маленького шарика (измеряют три диаметра одного шарика и берут среднее значение).

2. Осторожно опустить шарик через отверстие в крышке.

3. Одновременно с опусканием шарика в отверстие фиксируем глазом верхнюю метку. Кольцо должно сливаться в прямую линию.

4. При прохождении шарика через верхнюю метку включить секундомер.

5. Сразу же после прохождения шарика через верхнюю метку фиксируем глаз на нижней метке.

6. При прохождении шарика через нижнюю метку выключить секундомер.

7. По формуле (18) рассчитайте коэффициент вязкости.

8. Опыт провести 5 раз и результаты внести в таблицу 2.

9. Сравните полученные результаты с табличными данными. Сделайте выводы.

№ п/п	d (м)	ℓ (м)	t (с)	ρ (кг/м³)	ρ_ж (кг/м³)	g (м/с²)	η (Па∙с)	∆η (Па∙с)
1.
2.
3.
4.
5.
ср.

РАСЧЕТЫ И ВЫВОДЫ:

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Что такое вязкость жидкости?

2. Записать формулу Ньютона для силы внутреннего трения.

3. Что такое коэффициент динамической вязкости?

4. Чем отличается ламинарное течение от турбулентного?

5. Что такое кинематическая вязкость?

6. Что такое поток жидкости?

7. Запишите закон Пуазейля для скорости ламинарного течения.

8. В чем сущность метода Стокса?

9. Назвать силы, действующие на тело, движущееся в вязкой среде и указать их направление.

10. Первый закон Ньютона и его применение в данной лабораторной работе.

11. Качественное влияние температуры на коэффициент вязкости в жидкостях и газах.

12. Возможные применения метода Стокса.

13. Опишите капиллярный метод определения вязкости.

14. В чем сущность ротационного метода определения вязкости?

ЛАБОРАТОРНАЯ РАБОТА № 5

ДИФФУЗИЯ В ГАЗАХ

Цель работы : знакомство с компьютерной моделью, описывающей диффузию молекул идеального газа, экспериментальное подтверждение закона диффузии, экспериментальное определение средней скорости теплового движения частиц в данной модели.

Данная лабораторная содержит описания, в которых используются компьютерные модели, разработанные фирмой «Физикон».

Для начала работы необходимо дважды щелкнуть левой кнопкой мыши, когда ее маркер расположен над эмблемой сборника компьютерных моделей. После этого появится начальная картинка, имеющая вид

После этого необходимо дважды щелкнуть левой кнопкой мыши, установив ее маркер над названием радела, в котором расположена данная модель.

Выберите «Термодинамика и молекулярная физика», «Диффузия». Нажмите кнопку с изображением страницы во внутреннем окне.

КРАТКАЯ ТЕОРИЯ

При нарушении равновесия макросистема стремится вернуться в равновесное состояние.

Явлениями переноса называются процессы, связанные с возникновением в веществе направленного переноса (потока) массы, импульса или внутренней энергии.

Диффузия есть процесс установления внутри фаз вещества равновесного распределения концентраций, который обеспечивается направленным переносом массы этого вещества. Диффузия обусловлена тепловым движением молекул и проявляется в самопроизвольном выравнивании концентраций в смеси нескольких веществ.

Самодиффузия имеет место при самопроизвольном выравнивании концентрации однородного вещества, если по некоторым причинам равновесное распределение концентрации было нарушено.

Длина свободного пробега l есть среднее расстояние, пролетаемое частицей между двумя последовательными столкновениями.

Эффективный диаметр частицы есть минимальное расстояние, на которое сближаются центры двух сталкивающихся частиц.

Если в начальный момент времени имеет место неоднородное распределение плотности вещества r вдоль только одной оси (например, ОХ), тогда возникает одномерная диффузия, связанная с переносом массы М вдоль этой оси ОХ.

Для двухкомпонентной системы (например, смеси двух газов) одномерная диффузия описывается первым законом Фика:

где dM - масса одного компонента (индексы для характеристик данного компонента пропущены), которая переносится за время dt через элементарную площадку, перпендикулярную оси ОХ, имеющую площадь dS, в направлении убывания плотности этого компонента:

градиент плотности первого компонента;

D - коэффициент диффузии.

Для смеси «красных» и «зеленых» частиц, имеющих одинаковую массу m каждой частицы,

dM = m·dN; r = m , а ,

где dN - количество частиц, проходящих через dS за время dt, которое равно ,

где разность числа частиц в левом и правом сосудах

DN = N₂- N₁, N₂= N₀- N(t) , N₁= N(t);

DX = L_отв , объем сосуда V = 20 cм³ , dS есть площадь отверстия.

Решаем уравнение методом разделения переменных:

Интегрируем слева от 0 до N(t), а справа - от 0 до t и получаем:

или .

Обратите внимание на 2 системы частиц, находящихся в начальный момент в левом (красные) и в правом (зеленые) объемах. Они абсолютно упруго сталкиваются друг с другом и со стенками сосуда. Количество частиц N₀ каждой компоненты равно 100 и данная система является хорошей “механической” моделью идеального газа.

Нажмите мышью кнопку «Старт» во внутреннем окне экрана.

В процессе исследований можно останавливать движение всех молекул (при нажатии кнопки «½½» сверху во внешнем окне) и получать как бы “мгновенные фотографии”. Для продолжения наблюдений надо нажать кнопку «uu», расположенную сверху во внешнем окне. Количество частиц подсчитывается автоматически и высвечивается над соответствующими столбиками. Для установки нового диаметра трубки надо нажать «uu»сверху во внешнем окне и кнопки «Старт» и «Выбор» внизу во внутреннем окне.

Дата добавления: 2020-04-08; просмотров: 2766; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 456 7 Следующая ⇒

Мы поможем в написании ваших работ!