Оценка точности прямых измерений
МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА
РОССИЙСКОЙ ФЕДЕРАЦИИ
ФГБОУ ВО
« Белгородский государственный аграрный университет имени В.Я.Горина»
ПРАКТИКУМ
ПО ФИЗИКЕ
ДЛЯ СТУДЕНТОВ АГРОНОМИЧЕСКОГО ФАКУЛЬТЕТА
Белгород 2015
Удк 53(075.8)
ББК 22.3 я73
П69
Практикум по физике для студентов агрономического факультета./Составители А.Н.Акупиян, М.А.Шаршанова. – Белгород: Изд-во БелГАУ,2015.- 50с.
Рецензент – А.В. Сабылинский, канд. физ.-мат. наук, доцент кафедры физики БелГТУ им. Шухова.
© БелГАУ им. В.Я.Горина, 2015
Содержание:
| 1 | ЛАБОРАТОРНАЯ РАБОТА ОБРАБОТКА РЕЗУЛЬТАТОВ ФИЗИЧЕСКОГО ЭКСПЕРИМЕНТА | 4 |
| 2 | ЛАБОРАТОРНАЯ РАБОТА МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ | 13 |
| 3 | ЛАБОРАТОРНАЯ РАБОТА ОПРЕДЕЛЕНИЕ МОДУЛЯ УПРУГОСТИ ТВЕРДЫХ ТЕЛ | 18 |
| 4 | ЛАБОРАТОРНАЯ РАБОТА ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ВЯЗКОСТИ ЖИДКОСТИ | 28 |
| 5 | ЛАБОРАТОРНАЯ РАБОТА ДИФФУЗИЯ В ГАЗАХ | 37 |
| 6 | ЛАБОРАТОРНАЯ РАБОТА МАГНИТНОЕ ПОЛЕ | 43 |
ЛАБОРАТОРНАЯ РАБОТА № 1
ОБРАБОТКА РЕЗУЛЬТАТОВ ФИЗИЧЕСКОГО ЭКСПЕРИМЕНТА
Цель работы: ознакомление с методами оценки результатов измерений и
расчета погрешностей.
Приборы и принадлежности: исследуемые образцы; штангенциркуль;
микрометр.
КРАТКАЯ ТЕОРИЯ
|
|
|
Положения и выводы физики непосредственно связаны с экспериментом. Как и в любой точной науке, в физике результаты экспериментов представляются чаще всего набором некоторых чисел – числовых значений физических величин. Эти числовые значения, входящие в математическую формулу, устанавливают связь между физическими величинами в явлениях природы.
Измерить физическую величину – значит сравнить ее с единицей измерения. Измерение – это последовательность экспериментальных и вычисленных операций, осуществляемых для нахождения значения заданной физической величины. В зависимости от способа получения результата следует различать измерения прямые и косвенные.
При прямых измерениях результат получается непосредственно из измерений самой величины. Например, измерение длины стола линейкой, силы тока – амперметром, напряжения на участке цепи – вольтметром.
При косвенных измерениях результат получается после вычисленных операций, произведенных над результатами прямых измерений. Например, площадь стола можно найти по формуле:
 ,
,
где a и b – длина и ширина стола.
Косвенные измерения значительно сложнее, но они применяются довольно часто, особенно при экспериментальных исследованиях.
|
|
|
Измерения включают в себя следующие элементы:
‑ физический объект (например, цилиндр);
‑ технические средства измерений (например, штангенциркуль и микрометр);
‑ наблюдателя (или регистрирующее устройство), который воспринимает результат измерений.
Истинное значение физической величины абсолютно точно измерить нельзя. При измерении физических величин возникают погрешности измерений. Погрешностями измерений называют отклонения результатов измерений от истинного значения измеряемой величины. Все погрешности принято подразделять на систематические, случайные и промахи.
Промахи (грубые погрешности) возникают вследствие недосмотра наблюдателя или необнаруженной неисправности инструмента (прибора). Промахи исключаются из результатов измерений.
Случайные погрешности обусловлены как несовершенством органов чувств наблюдателя, так и условиями проведения эксперимента. Случайных погрешностей избежать нельзя. Их оценивают по данным многократных наблюдений методами математической статистики. Чем больше измерений сделано, тем ближе значение измеряемой величины к его истинному значению.
Систематические погрешности появляются вследствие неточности приборов и несовершенства методов измерений. Систематические погрешности не зависят от числа измерений. Они остаются постоянными в течение времени проведения эксперимента и могут быть исключены введением поправок.
|
|
|
Итак, систематические погрешности можно устранить или учесть, промахи следует отбросить, а случайные погрешности необходимо учитывать путем специальной математической обработки результатов измерений.
Погрешности приборов
В лабораторных работах метод измерений обычно задан, поэтому из систематических погрешностей учитываются только приборные.
Все приборы и инструменты, используемые для измерений физических величин: амперметр, вольтметр и т.д., характеризуются классом точности и (или) ценой деления. Класс точности K – это обобщенная характеристика прибора, показывающая относительную погрешность прибора выраженную в процентах. Класс точности обозначается числом на шкале прибора: 0.1; 0.2; 0.5; 1.0; 1.5; 2.5; 4. Приборы класса точности 0.1; 0.2; 0.5 применяются для точных измерений и называются прецизионными. В технике применяют приборы классов 1.0; 1.5; 2.5; 4, которые называются техническими. Если на шкале прибора класс точности не указан, то данный прибор внеклассный, то есть имеет большую погрешность измерений.
|
|
|
Абсолютная систематическая погрешность ∆Хпр прибора
 , (1)
, (1)
где  – наибольшее значение физической величины, которое может быть измерено по шкале прибора.
– наибольшее значение физической величины, которое может быть измерено по шкале прибора.
Если класс точности прибора не известен, то его абсолютная систематическая погрешность  принимается равной половине цены наименьшего деления
принимается равной половине цены наименьшего деления  шкалы:
шкалы:
 . (2)
. (2)
Например, при измерении линейкой, наименьшее деление которой 1мм допускается погрешность 0.5мм.
Для приборов, оснащенных нониусом, за приборную принимают погрешность, определяемую нониусом. Для штангенциркуля (рис.1.) – 0.1мм, 0.02 мм или 0.05мм; для микрометра (рис. 2.) – 0.01мм.
Штангенциркуль – прибор для наружных и внутренних измерений. Он построен по принципу штанги 1 с основной шкалой, представляющей собой миллиметровую линейку, и подвижной рамки 2 с нониусом 3 (рис.1.). Рамка может передвигаться по штанге. Закрепление рамки на штанге осуществляется с помощью винта 4. Нониус ‑ это вспомогательная шкала штангенциркуля, расположенная на рамке и служащую для отсчета долей миллиметра. В нашей стране стандартизированы штангенциркули с нониусами 0.1; 0.05; и 0.02 мм. Отсчет размеров производится по основной шкале и нониусу.
На рис. 1. представлен штангенциркуль с нониусом 0.05мм. Шкала этого нониуса получена при делении 39 мм на 20 частей. Следовательно, каждое деление нониуса равно 1.95 мм, то есть на 0.05 мм меньше делений основной шкалы. Если расположить нониус ровно так, что первый штрих нониуса совпадет с первым штрихом основной шкалы, то основное деление нониуса отойдет от основного деления шкалы на 0.05 мм. Для получения нониуса с ценой деления 0.1 мм делят 19 мм на 10 частей (19 мм : 10 = 1.9 мм), тогда каждое деление нониуса будет на 0.1 мм меньше, чем 1 мм.

| 1 |
| 3 |
| 2 |
| 4 |
| 5 |
| 6 |

Рис. 1. Штангенциркуль
Измеряемый предмет располагают между ножками 5, 6 штангенциркуля и закрепляют винтом 4. Целые значения в миллиметрах отсчитывают по основной шкале от «0» основной шкалы до «0» нониуса. Затем смотрят, какое деление нониуса совпало с делением основной шкалы. Если номер совпавшего деления нониуса умножить на цену деления прибора, то получаются сотые доли миллиметра. Если с делением основной шкалы совпадает нулевое или последнее деления нониуса, то сотых долей не будет.
На рис. 2. представлены измерения штангенциркуля с нониусом 0.05 мм.

| размер 6,70 мм |

| размер 25,30 мм |

Рис. 2.
Микрометр – это инструмент, применяемый для точных измерений. Принцип действия микрометра основан на работе винтовой пары, то есть преобразования вращательного движения в поступательное.
В скобе 1 микрометра при вращении барабана 2 перемещается микрометрический винт 3, между торцом которого и пяткой 4 помещают измеряемую деталь (рис. 3.). Шаг микрометрического винта равен 0.5 мм, а конусная поверхность барабана разделена на 50 равных частей. Следовательно, поворот барабана на одно деление соответствует перемещению винта на 0,01мм. Вращения барабана нужно производить с помощью трещотки 5, обеспечивающей постоянное усилие на измеряемую деталь. Зажим детали про 
| 1 |
| 4 |
| 6 |
| 2 |
| 3 |
| 5 |

Рис. 3. Микрометр
На стебле 6 микрометра расположены две шкалы. Деления нижний шкалы нанесены через 1 мм, деления верхней шкалы расположены посередине между штрихами нижней шкалы. По нижней шкале отсчитывают целые миллиметры, а по верхней ‑ половину миллиметра. При измерении встречаются два характерных случая. В первом случае (рис. 4.) деления нижний шкалы расположены ближе к барабану, нежели деления верхней шкалы. При этом целые значения миллиметров отсчитываются по нижней шкале, а сотые доли ‑ по барабану. Например, показания инструмента соответствуют размеру 18.04 мм. Во втором случае деление верхней шкалы расположены ближе к барабану, чем деление нижней шкалы. При этом учитываются целые, половинка и сотые доли миллиметра. Например, показания инструмента соответствует размеру 18 целых + половинка 0.50 + 9 сотых, то есть 18,59 мм.

| размер 18,04 мм |

| размер 18,59 мм |

Рис. 4.
Оценка точности прямых измерений
Для наиболее точного определения искомой физической величины измерение ее значения производят несколько раз. При многократном измерении возможно получение результата как большего, так и меньшего, чем истинное значение измеряемой величины.
Пусть величину Х измеряли n раз и получали множество значений:
 , (3)
, (3)
i – номер измерения.
Хорошим приближением к истинному значению измеряемой величины является его среднеарифметическое значение ‹X›:

| å |
| = |
| = |
| + |
| + |
| + |
| + |
| = |
| ñ |
| á |
| » |
| n |
| i |
| i |
| n |
| ист |
| Х |
| n |
| n |
| Х |
| Х |
| Х |
| Х |
| Х |
| Х |
| 1 |
| 3 |
| 2 |
| 1 |
| 1 |
| ... |
| . |
Абсолютная случайная погрешность ∆Хсл n‑измерений имеет размерность измеряемой величины и определяется по формуле:

Для оценки суммарной абсолютной погрешности измерений ∆X необходимо знать случайную составляющую погрешности ∆Хсл и систематическую составляющую погрешности ∆ X пр.
Тогда:  (6)
(6)
и результат измерений записывается в виде:
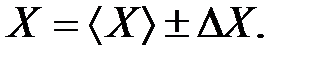 (7)
(7)
Абсолютная погрешность ∆X не дает полной информации о точности измерений. Поэтому результат оценивается еще и относительной погрешностью δX, показывающей, какая часть абсолютной погрешности приходится на каждую единицу измеряемой величины.
Относительная погрешность равна отношению абсолютной погрешности к среднеарифметическому значению измеряемой величины.
 (8)
(8)
Результат измерений физической величины считается хорошим, если относительная погрешность не превышает 5% .
Дата добавления: 2020-04-08; просмотров: 217; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
