Допущения, принимаемые при расчетах на прочность

⇐ ПредыдущаяСтр 3 из 10Следующая ⇒

-материал деталей обладает способностью полностью восстанавливать первоначальные форму и размеры тела после устранения причин, вызвавших его деформацию, т. е. обладает свойством идеальной упругости.

– Материал деталей является однородным и сплошным, т. е. свойства материала не зависят от размера и формы детали и одинаковы во всех ее точках, будь это композиционный материал, пластмасса или сплав.

– Материал детали изотропен, т.е. обладает во всех направлениях одинаковыми свойствами. Различие свойств в разных направлениях (анизотропия) учитывают при расчете деревянных деталей.

– В теле до приложения нагрузки нет начальных внутренних сил, т. е. отсутствуют напряжения.

– Деформации тела очень малы по сравнению с его размерами и не оказывают влияния на взаимное расположение нагрузок.

– Деформации материала в каждой его точке прямо пропорциональны напряжениям в этой точке (закон Гука).

– Принцип независимости действия сил (принцип наложения) – результат воздействия на тело системы сил равен сумме результатов воздействия тех же сил, прилагаемых к телу отдельно в любом порядке.

Деформация растяжения-сжатия?

Стержень испытывает деформацию растяжения, длина его увеличилась на величину ,

а ширина уменьшилась на величину 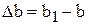, где ℓ₁, b ₁– соответственно длина и ширина стержня после приложения сил. Величины Δℓ и Δ b называют абсолютным удлинением и сужением стержня или абсолютной продольной и поперечной деформацией. Величину ε = Δℓ/ ℓ называют относительной линейной деформацией или относительным удлинением.\\ Соответственно ε₁ = Δ b / b называется относительной поперечной деформацией.\\ Абсолютная величина отношения относительной поперечной деформации ε₁ к относительной продольной деформации ε называется коэффициентом поперечной деформации, или коэффициентом Пуассона μ = | ε₁/ ε |,который характеризует упругие свойства материала, его способность к поперечным деформациям.// деформации и напряжения во всех точках поперечного сечения одинаковы.\\\\ Из уравнения равновесия в проекциях сил на продольную ось стержня определим, что N = F. Составляющая внутренних сил N направлена по нормали к поперечному сечению, поэтому в сечении действуют нормальные напряжения, величина которых определяется с учетом равномерного распределения их по сечению как σ = N / S = F / S, где S(А*) – площадь поперечного сечения стержня. \\\При упругих деформациях справедлив закон Гука, устанавливающий линейную зависимость между напряжением и деформацией, σ = E·ε. Коэффициент пропорциональности Е называют модулем упругости материала (модулем Юнга)\\\ Подставив в выражение, значения σ, и ε, получим формулу для определения абсолютного удлинения стержня Δℓ = (N·ℓ)/ (E·A)

Произведение Е·А характеризует сопротивляемость стержня к удлинению (сжатию) и называется жесткостью стержня при растяжении (сжатии).

20/ Определение механических свойств материалов. Диаграмма напряжений

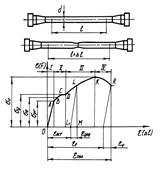
Свойства материалов при расчетах на прочность, жесткость и устойчивость определяются механическими характеристиками.\\Мех хар матер можно определить нагружая образцы, до разрушения или значительной деформации, при любом виде нагружения.\\\ Наибольшее распространение имеют испытания на растяжение\\ На специальных машинах растягивают образцы (рис. 5.8, а), размеры которых ограничены стандартом, записывая автоматически зависимость изменения растягивающей силы F от удлинения образца Δℓ , т.е. диаграмму растяжения в координатах F = f(Δℓ).\\\ Известно, что величина растягивающей силы F и величина удлинения Δℓ образцов из одного материала зависят от их размеров.\\\ Чтобы можно было сравнить результаты испытаний образцов различных размеров, диаграмму растяжения перестраивают в координатах σ = F / S и ε = Δℓ/ ℓ , где S – первоначальная площадь сечения образцов; ℓ – первоначальная длина рабочей части образца. Эту диаграмму σ = f (ε) называют диаграммой напряжений или условной диаграммой растяжения, определяется свойствами материала.\\\ Участок длиной ОА до некоторого напряжения σ _pr , называемого пределом пропорциональности, представляет прямую линию. На этом участке справедлив закон Гука и величина абсолютной деформации Δℓ прямо пропорциональна растягивающему усилию F , а относительная деформация ε – напряжению σ.==Точке В(начало появл остаточ напряжен) соответствует предел упругости материала σ _e * – то наибольшее напряжение, до которого в материале появляются только упругие деформации.(ε_ост≈0,05%)== Точка С. Для таких материалов пределу текучести σ _y соответствует напряжение, при котором остаточная деформация равна 0,2%. Поэтому иногда предел текучести обозначают σ _0,2 и называют условным пределом текучести. (ε_ост≈0,2%)== Точка К диаграммы соответствует наибольшей по величине нагрузке, а напряжение, соответствующее этой точке (наибольшей по величине нагрузке), называется пределом прочности σ _u *** или временным сопротивлением и обозначается при растяжении σ _ut****.\\\\ Кроме перечислимых выше прочностных характеристик при испытании на растяжение определяют характеристики пластичности материала, т.е. способности материала получать не разрушаясь большие остаточные деформации: относительное остаточное удлинение при разрыве 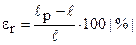и относительное остаточное сужение при разрыве ,где ℓ _p, A_p – соответственно расчетная длина образца и площадь поперечного сечения в наиболее тонком месте шейки после разрыва.

21/ Твердость материалов

На производстве при необходимости быстрого контроля свойств изготавливаемых деталей, например, контроля прочности после термической или термохимической обработки, метод испытания образцов на растяжение имеет много неудобств.

Твердость (Н)– способность материала оказывать сопротивление проникновению в него инородного тела.

Метод Бринелля основан на вдавливании в поверхность испытуемого материала стального закаленного шарика(НВ) диаметром 2,5; 5 или 10 мм под действием силы F, приложенной перпендикулярно к поверхности изделия в течение определенного времени. Числом твердости по Бринеллю называется отношение нагрузки F к площади сферического отпечатка S, т.е. HB=F/ S. Твердость по Бринеллю при условиях испытания, когда диаметр шарика 10 мм, F = 3000 кгс и продолжительность выдержки под нагрузкой от 10 до 15 с, обозначается цифрами, характеризующими число твердости, и буквами НВ. Например, 120НВ, где 120 – число твердости в кгс/мм²; НВ – твердость по Бринеллю. \\ Достоинства: Достаточная быстрота испытания, простота и надежность прибора, отсутствие необходимости тщательноц подготовки поверхности. Недостатки: ограничение НВ<450/\\\\

О твердости по методу Роквелла( HR ) судят по разности глубин, на которые проникает алмазный конус с углом при вершине 120° или стальной закаленный шарик диаметром 1,588 мм при действии двух последовательно приложенных нагрузок: предварительной величиной 10 кгс и общей – 60, 100 или 150 кгс, равной сумме предварительной и основной нагрузок. Для определения числа твердости применяют три шкалы. Шкала В соответствует вдавливанию шарика и число твердости при этом обозначается HRB. Для более твердых материалов применяются шкалы А и С_э, соответствующие вдавливанию алмазного конуса. Вначале индентор вдавливается в поверхность образца под предварительной нагрузкой, которая не снимается до конца испытаний, что обеспечивает точность измерений. Затем подается основная нагрузка (для шкалы А – 50 кгс, для шкалы В – 90 кгс, для шкалы С – 140 кгс), после снятия которой число твердости определяют глубиной отпечатка. Достоинства: совмещение операций вдавливания индентора и измерения размеров отпечатка, универсальности, небольшому размеру отпечатка. Недостатки: подготовка поверхности, условный и безразмерный численный результат . HR <170/ \ \\ 1 HRC ≈ 10 НВ.

Метод измерения твердости по Виккерсу ( HV ) заключается во вдавливании в испытываемый материал правильный четырехгранной алмазной пирамиды с углом в 136° между противоположными гранями. Число твердости по Виккерсу вычисляется путем деления нагрузки на площадь поверхности пирамидального отпечатка HV=F/S.

Достоинства: алмазный индентор, сам отмечаток, размерность 1 HV ≈ 1 НВ

22/ Допускаемые напряжения. Условия прочности и жесткости конструкций

При расчетах на прочность нагруженных деталей необходимо подобрать размеры поперечных сечений такими, чтобы детали не могли получить недопустимую при работе деформацию или разрушиться. Это обеспечивается соблюдением условий прочности и жесткости. Согласно условию прочности максимальные действительные напряжения, возникающие вследствие действия внешних сил, не должны превышать допускаемых. По условию жесткости должны быть ограничены величины деформаций: абсолютная или относительная действительная деформация не должна превышать допускаемую.

Допускаемыми называют напряжения, соответствующие деформациям, допустимым при работе механизма. Допустимые деформации деталей ограничивают упругими деформациями. Так как величины допускаемых напряжений определяются величиной допустимых деформаций, при расчетах обычно используют условие прочности, которое включает в себя условие жесткости. Условия прочности по нормальным и касательным напряжениям имеют соответственно вид

σ_max ≤ σ_adm; τ_max ≤ τ_adm, (5.13)

где σ _max, τ _max – соответственно максимальные нормальные, касательные напряжения; σ _adm, τ _adm* – соответственно допускаемые нормальные, допускаемые касательные напряжения.

Допускаемое напряжение связывают с механическими свойствами материала детали и определяют по формуле σ_adm = σ_u/ n, (5.14)

где σ _u – предельное напряжение для материала, т.е. напряжение, при котором могут появиться заметные остаточные деформации: для пластичных материалов в качестве такового принимают условный предел текучести σ_0,2 или предел текучести σ _y, а для хрупких материалов – предел прочности σ _u; n – коэффициент запаса прочности, представляемый в виде произведения n = n₁n₂n₃…, который всегда больше единицы и учитывает разброс механических свойств материала, неточное знание действующих нагрузок, возможные перегрузки при эксплуатации, влияние концентраторов напряжений, габаритов детали, последствий разрушения или выхода ее из строя и других факторов. Чем больше коэффициент запаса прочности, тем надежнее деталь в работе, но превышение n определенной величины ведет к чрезмерному увеличению габаритов и веса, что экономически невыгодно. Правильный выбор коэффициента запаса прочности n является важным этапом при расчетах на прочность. Для пластичных материалов принимают n ≈ 1,4 … 1,6, для хрупких – 2,5 … 3,0. \\\Допускаемое касательное напряжение τ _adm материала принимается как часть допускаемого нормального напряжения: для пластичных материалов (конструкционных сталей, сплавов меди и алюминия) τ_adm = (0,5 .. 0,6)σ_adm, для хрупких материалов τ_adm = (0,8 … 1,0)σ_adm.

Условием прочности при растяжении (сжатии) будет выражение σ = N / A ≤ σ _adm. (5.15)

С его помощью можно решить следующие задачи: – Проверить прочность нагруженного стержня, т.е. по заданной нагрузке и размерам поперечного сечения определить действительные напряжения и сравнить их с допускаемыми . – Определить размеры поперечного сечения стержня по известной нагрузке и допускаемому напряжению материала A ≥ N/ σ_adm. – Определить допускаемую продольную силу по заданным размерам А поперечного сечения стержня и допускаемому напряжению материала стержня N ≤ A·σ_adm.\\\Далее, зная связь между продольной силой N и внешними силами F, можно найти предельную внешнюю нагрузку F_u. – Выбрать материал нагруженного стержня по заданным размерам А поперечного сечения стержня и нагрузке, приняв или рассчитав величину коэффициента запаса прочности n: σ_0,2 = n· σ_adm ≥ (n N)/ A.

Стержни, испытывающие деформацию сжатия, кроме расчета на прочность необходимо рассчитывать и на устойчивость (продольный изгиб), чтобы не произошло выпучивания и потери устойчивости сжатого стержня.

Отметим, что при действии на стержень системы внешних сил продольная сила N в поперечном сечении равна алгебраической сумме внешних продольных сил, действующих по одну сторону от сечения.

Деформация сдвига(Среза)?

При простом растяжении две части стержня, разделенные наклонным сечением, стремятся не только оторваться, но и сдвинуться одна относительно другой. Сдвигу противодействуют касательные напряжения, действующие в плоскости сечения.

На практике ряд деталей работает в таких условиях, когда причиной их разрушения является сдвиг одной части детали относительно другой. При расчете на прочность таких деталей учитываются касательные напряжения и расчет на прочность ведется по ним. Пусть к стержню приложены перпендикулярно его продольной оси две равные по модулю, но противоположно направленные силы, действующие очень близко друг от друга (рис. 5.13, а). При достаточной величине этих сил произойдет срез – отделение правой части стержня относительно левой по сечению I – I. Деформации среза в зоне действия усилий предшествует перекашивание прямых углов элементарного объема – параллелепипеда с ребрами abd с (5.13, б). На гранях параллелепипеда возникают касательные напряжения, направление которых определяется законом парности касательных напряжений. Если нормальные напряжения вызывают линейные деформации (удлинения и укорочения), то касательные напряжения вызывают угловые деформации γ, так называемые углы сдвига. При равенстве касательных напряжений по площадкам элементов деформированного тела (закон парности касательных напряжений) имеем одинаковые угловые деформации, углы сдвига.

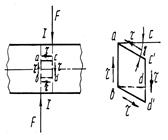
Чистым сдвигом называют такое напряженное состояние, когда по граням элемента в виде бесконечно малого кубика действуют только касательные напряжения. Например, чистый сдвиг наблюдается во всех точках скручиваемого стержня с круглым поперечным сечением.

Пользуясь методом сечений, определим, что равнодействующая внутренних сил в плоскости I – I (плоскости сдвига) (рис. 5.13, а) равна внешней силе F, т.е. Q = F . Это усилие может вызвать лишь касательные напряжения, равномерно распределенные по плоскости сечения. Поэтому

τ = Q/A = F/A, (5.26)где А – площадь поперечного сечения стержня.

Действительное распределение касательных напряжений по сечению I – I не является равномерным, в узких краевых зонах касательные напряжения приближаются к нулю. Но это обстоятельство при инженерных расчетах не принимается во внимание, так как область указанных отклонений мала по сравнению с размерами сечения.

Опыты показывают, что для большинства материалов до определенных величин нагружения имеется линейная зависимость между напряжениями и деформациями при сдвиге, которую выражает закон Гука: τ = G·γ, (5.27) где G – модуль упругости материала при сдвиге, или модуль упругости второго рода. Он связан с модулем упругости E при растяжении через коэффициент Пуассона μ следующей зависимостью:G = E/[2(1 + μ)]. Отметим, что для стали G ≈ 8·10⁴ МПа, для алюминия G ≈ 2,7·10⁴ МПа.

Так как разрушение детали при деформации сдвига называют срезом, расчет на прочность при данной деформации называют расчетом на сдвиг или на срез. Примером соединений, рассчитываемых на срез, являются заклепочные, болтовые, сварные, паяные, клеевые соединения.

Условие прочности при сдвиге имеет вид τ = Q / A ≤ τ _adm, (5.28)где Q – равнодействующая внутренних сил в плоскости сдвига; А – площадь сдвига; τ _adm – допускаемое касательное напряжение материала детали.

24/ Моменты инерции плоского сечения (прямоугольника, круга)

Полярным моментом инерции сечения называется взятая по всей площади сечения сумма произведений площадей элементарных площадок на квадрат их расстояния до данного полюса (точки). Из рис. 5.15

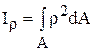, (5.35)

где ρ – расстояние от площадки dA до полюса (точки 0).

Рис. 5.15 Рис. 5.16

Осевым моментом инерции сечения называется взятая по всей площади сечения сумма произведений площадей элементарных площадок на квадрат их расстояния до оси. Так, моменты инерции сечения относительно координатных осей z и y будут соответственно равны

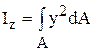, (5.36) 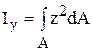. (5.37)

Так как ρ² = z² + y², сравнив выражения (5.35), (5.36) и (5.37), получим I_ρ = I_z + I_y, (5.38)

т.е. сумма осевых моментов инерции сечения относительно двух взаимно перпендикулярных осей равна полярному моменту инерции этого сечения относительно точки пересечения рассматриваемых осей. Моменты инерции сечений – всегда положительные величины.

Дата добавления: 2020-01-07; просмотров: 419; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 234 5 6 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!