Билет 6. Приведение системы сил к простейшему виду.
1. Равновесие
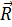 =0 ,
=0 , 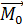 =0
=0 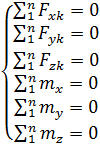
а) плоская система сил 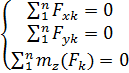
б) система параллельных сил 
в) сходящаяся система сил 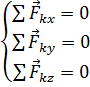
. 
2. 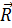 ≠0 ,
≠0 , 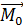 =0
=0
В данном случае система сил сводится к равнодействующей, равной гл. вектору и приложенной в данном центре приведения.
3. 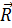 =0 ,
=0 , 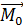 ≠0
≠0
Система сводится к паре сил с моментом, равным главному моменту и не зависит от центра приведения.
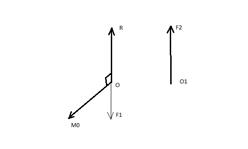
4. . 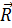 ≠0 ,
≠0 , 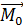 ≠0
≠0
а) 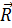 перпендикулярен к
перпендикулярен к 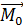
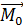 =
= 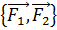
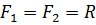
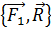 -уравниваем систему
-уравниваем систему
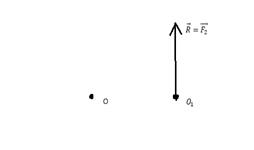
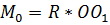
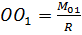 (1)
(1)
Когда 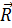 перпендикулярен к
перпендикулярен к 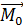 систему сил можно привести к равнодействующей, равной гл. вектору и приложенной в новом центре приведения, найти который можно по ф.(1)
систему сил можно привести к равнодействующей, равной гл. вектору и приложенной в новом центре приведения, найти который можно по ф.(1)
б) 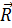 НЕ перпендикулярен к
НЕ перпендикулярен к 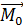
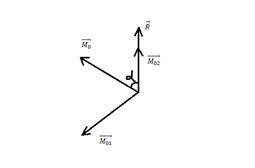 Разложим
Разложим 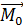 на
на 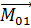 и
и 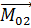
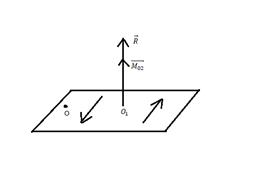
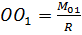
Систему сил вида « 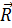 НЕ перпендикулярен к
НЕ перпендикулярен к 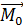 » можно привести к виду: 3 силы- 1 сила-это
» можно привести к виду: 3 силы- 1 сила-это 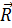 и пара сил, параллельных к плоскости. Такая система сил называется-винт.
и пара сил, параллельных к плоскости. Такая система сил называется-винт.
Билет 7. Центр параллельных сил. Центр тяжести тела.
Точка С, через которую проходит линия действия равнодействующей силы параллельных сил при любых поворотах этих сил около их точек приложения в одну и ту же сторону и на один и тот же угол, называется центром параллельных сил.
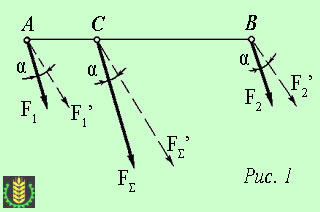
Формулы для определения координат центра параллельных сил:
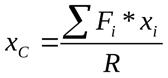
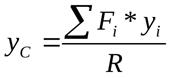
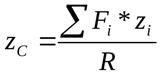
Центр тяжести тела.
Центром тяжести тела называется геометрическая точка, жестко связанная с этим телом, и являющаяся центром параллельных сил тяжести, приложенных к отдельным элементарным частицам тела.
|
|
|
Координаты центра тяжести неоднородного твердого тела в выбранной системе отсчета определяются следующим образом:
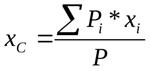
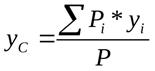
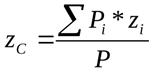
Если тело объемное, то P=j*V
Если тело плоское, то P=j*S
Если тело линейное, тоP=j*L
Билет 8. Кинематика. Способы задания движения точки. Касательное и нормальное ускорение точки.
Кинематикой называется раздел механики, в котором изучается геометрические свойства движения тел без учета их инертности (массы) и действующих на них сил.
Кинематически задать движение или закон движения тела (точки) - значит задать положение этого тела (точки) относительно данной системы отсчета в любой момент времени.
Непрерывная линия , которую описывает движущаяся точка относительно данной системы отсчета, называется траекторией точки. Если траекторией является прямая линия, движение точки называется прямолинейным, а если кривая - криволинейным.
Способы задания движения точки.
Для задания движения точки можно применить один из следующих трёх способов:
* Векторный
* Координатный
* Естественный
1. Векторный способ задания движения точки.
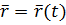
Это равенство определяет закон движения точки в векторной форме, так как оно позволяет в любой момент времени построить соответствующий вектор 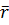 и найти положение движущейся точки. В прямоугольных декартовых координатах для вектора
и найти положение движущейся точки. В прямоугольных декартовых координатах для вектора 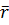 будет:
будет: 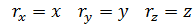 , где x , y , z – декартовы координаты точки.
, где x , y , z – декартовы координаты точки.
2. Координатный способ задания движения точки.
|
|
|
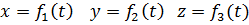
Эти уравнения представляют собой уравнения движения точки в прямоугольных декартовых координатах. Они определяют закон движения точки при координатном способе задания движения.
Если движение точки происходит все время в одной и той же плоскости , то, приняв эту плоскость за плоскость Oxy, получим в этом случае два уравнения движения: 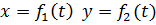
При прямолинейном движении точки, если вдоль ее траектории направить координатную ось Ox, движение будет определяться одним уравнением (законом прямолинейного движения точки) 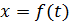
3. Естественный способ задания движения точки.
Естественным (или траекторным) способом задания движения удобно пользоваться в тех случаях, когда траектория известна заранее.
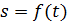
Это уравнение выражает закон движения точки вдоль траектории.
Чтобы задать движение точки естественным способом, надо задать:
1) Траекторию точки
2) Начало отсчета на траектории с указанием положительного и отрицательного направлений отсчета
|
|
|
3) Закон движения точки вдоль траектории в виде 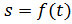
Касательное и нормальное ускорение точки.
Теорема Проекция ускорения точки на касательную равно первой производной от числового значения скорости или второй производной от расстояния (криволинейной координаты) s по времени, а проекция ускорения на главную нормаль равна квадрату скорости, деленному на радиус кривизны траектории в данной точке кривой; проекция ускорения на бинормаль равна нулю.
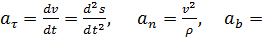 0
0
Дата добавления: 2020-01-07; просмотров: 163; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
