Показательное распределение (экспоненциальное)
Это распределение которое описывается деф.функцией вида: 
Где  -параметр деф.функции
-параметр деф.функции  и
и  ,
,  таким образом показательное распределение в отличии от нормального задается только
таким образом показательное распределение в отличии от нормального задается только  . В качестве примера НСВ которая подчиняется показательному закону распределения можно привести временной интервал появления 2х последовательных событий простейшего потока.
. В качестве примера НСВ которая подчиняется показательному закону распределения можно привести временной интервал появления 2х последовательных событий простейшего потока.
Интегральная функция:  На практике часто становится задача отыскания вероятности попадания в (a,b) НСВ Х подчиняющейся показательному закону распределения вероятности который задан интегральной функцией вида
На практике часто становится задача отыскания вероятности попадания в (a,b) НСВ Х подчиняющейся показательному закону распределения вероятности который задан интегральной функцией вида 
Для решения данной задачи  с учетом того что
с учетом того что 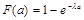
 получаем
получаем  значение функции затабулировано.
значение функции затабулировано.
Найдем Мат.ожидание НСВ Х распределенной по показательному закону:  в результате 2го интегрирования получаем
в результате 2го интегрирования получаем 
Дисперсия НСВ Х распределенной по показательному закону:  полученный интеграл находим двукратного применения формулы интегрирования по частям
полученный интеграл находим двукратного применения формулы интегрирования по частям 
Среднеквадратическое отклонение НСВ Х: 
40. Функцией надежности R ( t ) называют функцию, определяющую вероятность безотказной работы устройства в течение времени t. Функция надежности.
Пусть элемент (то есть некоторое устройство) начинает работать в момент времени t 0 = 0 и должен проработать в течение периода времени t . Обозначим за Т непрерывную случайную величину – время безотказной работы элемента, тогда функция F(t) = p(T > t) определяет вероятность отказа за время t. Следовательно, вероятность безотказной работы за это же время равна
|
|
|
R(t) = p(T > t) = 1 – F(t).
Эта функция называется функцией надежности.
Показательный закон надежности.
Часто длительность безотказной работы элемента имеет показательное распределение, то есть
F(t) = 1 – e - λt .
Следовательно, функция надежности в этом случае имеет вид:
R(t) = 1 – F(t) = 1 – (1 – e-λt) = e-λt .
Показательным законом надежности называют функцию надежности, определяемую равенством
R(t) = e - λt ,
где λ – интенсивность отказов.
Интегральная функция распределения двумерной СВ.
Пусть (ХУ) –двумерная СВ а ху пара действительных чисел. Обозначим через F(x,y) – вероятность события состоящего в том что СВ Х примет значение <х и в тоже время СВ У <у при изменении чисел х, у будет изменятся F(x,y) т.е F(x,y) рассматривается как функция от х и у.
Интегральная функция распределения двумерной СВ – это функция F(x,y) которая для каждой пары чисел (x,y) определяет вероятность того что СВ Х примет значение<х и в тоже время СВ У <у : 
Свойства:
1)значение интегральной функции F(x,y) удовлетворяет:  . Док-во: в основе данного свойства лежит определение интегральной функции как вероятности т.е вероятность – это всегда неотрицательное число и меньше 1
. Док-во: в основе данного свойства лежит определение интегральной функции как вероятности т.е вероятность – это всегда неотрицательное число и меньше 1
|
|
|
2) интегральная функция F(x,y) является неубывающей функцией по каждому аргументу:  если x2>x1
если x2>x1  если y2>y1
если y2>y1
3) для интегральной функции распределения двумерной СВ справедливо:  ;
;  ;
; 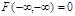 ;
; 
4) при  интегральная функция F(x,y) системы двух СВ становится интегральной функцией компонента х:
интегральная функция F(x,y) системы двух СВ становится интегральной функцией компонента х:  , при
, при 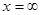 интегральная функция F(x,y) системы двух СВ становится интегральной функцией компонента y
интегральная функция F(x,y) системы двух СВ становится интегральной функцией компонента y  .
.
При помощи интегральной функции F(x,y) системы СВ Х и У можно рассматривать и рассчитать вероятность того что в результате эксперемента случайная точка попадает в полуполосу 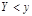
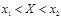 . для определения вероятности попадания случайной точки в полуполосу у применяют формулу :
. для определения вероятности попадания случайной точки в полуполосу у применяют формулу : 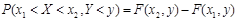
Для определения вероятности попадания случайной точки в полуполосу х:  следовательно вероятность попадания случайной точки в полуполосу рассчитывается как приращения интегральной функции системы 2х СВ по одному из аргументов.
следовательно вероятность попадания случайной точки в полуполосу рассчитывается как приращения интегральной функции системы 2х СВ по одному из аргументов.
Деф.функция двумерной НСВ.
Двумерная НСВ может быть задана не только при помощи интегральной но и при помощи деф.функции распределения вероятностей.
Деф.функция распределения двумерной НСВ Х и У это вторая смешенная частная производная от интегральная функции F(x,y): 
|
|
|
Если известна деф.функция f(x,y) двумерной СВ то интегральную функцию F(x,y) можно рассчитать по формуле 
Свойства:
1) деф.функция f(x,y) является неотрицательной 
2) двойной несобственный интеграл с бесконечными пределами от деф.функции =1 
3) если все возможные значения (x,y) принадлежат конечной области Д то 
Дата добавления: 2020-01-07; просмотров: 371; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
