Теорема полной вероятности. Формулы Байеса.

⇐ ПредыдущаяСтр 2 из 7Следующая ⇒

Вероятность события А, которое может наступить при условии 1го из несовершенных событий В1В2…В4 образующих полную группу, равна сумме произведений вероятностей из этих событий на соответствующую условную вероятность события А, которая называется формулой полной вероятности.

P(A)=P(B1)*P(A/B1)+P(B2)*P(A/B2)+…+P(Bn)*P(A/Bn)=∑ P(Bi)*P(A/Bi)

Пусть имеется событие А в которой может произойти при наступлении 1го и только 1го события В1В2…Вn из некоторой полной группы попарно несовершенных событий необходимо найти вероятность события Bi при условии что событие А уже наступило. По теореме умножения вероятности следует

P(B1A)=P(Bi)*P(A/Bi)/P(A) (1)

Применяет знам-лю последовательного равенства формулу полной вероятности

P(BiA)=P(Bi)*P(A/Bi)/∑P(Bi)*P(AB).

Локальная теорема Лапласа.

Если вероятность р-наступления события А в каждом испытании постоянна отлична от 0 и до 1,то вероятность Pn(m) того что событие появится в n-испытаниях , равно m-раз приближенно ровна тем точнее чем больше n приближенно знач.функции.

Для положения значения аргумента х значения

Определяется с помощью спец.таблиц,т.к. ф(х)-четная,то для значения аргумента х испытаний те же таблицы.

Вероятность отклонения относительной частоты от постоянной вероятности в независимых испытаниях.

При осущ. при n-независимых испытаний в которых из n вероятность появ. событий постоянна u=p(0<p<1), тогда вероятность того, что отклонение относительной частоты от постоянной вероятности p по абсолютной величине не превышает заданного числа ε >0 т.е. необходимо найти вероятность осущ .неравенства:

|m/n-p|≤ε

Искомую вероятность обозначим р(|m/n-p|≤ε)Для нахожд.ее заменим ему равносильным

Умножим на

Получим неравенство равносильное исходному

Распределение случайной величины.

Эта функция F(x) которая определяется на множестве действительных чисел равенством F(x)=P(X<x).Геометрическая интерпретация функции х распределения случайной величины х для каждого значения х и функция F(x)=вероятности случайногот события заключается в том что х примет значение в интервале от (-бесконечность;х).Областью определения функции распределения яв.множество действий чисел, а обл.измерения отрезок [0;1]

Свойсто функций распределения случайной величины

2)F(x) явл неубывающей т.е. Х1≤Х2

3) F(x)непрерывна слева

4)Если Х1<Х2,то P(X1≤X≤X2)=F(x2)-F(x1)

При изв. ряде распределения дискретной случайной величины функцию распределения данной величины можно поставить следующим образом

F(x)=F{x<x}=∑xi<x, где ∑{x=xi} означ. ∑ всех возможных значений xi случ. Величины х которое меньше х.

11)Определение случайной величины. Дискретныенепрерывные случайные величины. Закон распределения дискретной случайной величины.

Случайной величиной называется- величины которые в результате испытаний могут принимать те или иные возможные значения за раннее неизвестное. Случайные величины обознач прописными буквами X,Y,Z.А их возможное значение строчными буквами x,y,z.

Дискретной или непрерывной случайной величы-наз случайную величину X которая может принимать конечное множество или счетное число значений х1,х2,х3…Хn.

Непрерывной случайной величиной называется- случайные величины х которые могут принимать все значения из конечного или бесконечного промежутка.Для описания дискретной случайной величины необходимо не только указать все ее значения но и перечислить их вероятности.

Закон распределения дискр случ величины – это соотношение между возможными значениями х1,х2…Хn случайной величины х.закон случайной величины записывается в табличном виде,где 1ая строка содержит возможные значения,а 2ая их вероятности.

Последовательные независимые испытания. Схема Бернули.

Для вычисления вероятности: Pn(m) необходимо учесть что число различных произведений содержат:m-элементов, которые можно составить из n-элементов =числу сочетаний из n по m

Применяя m сложения вероятностей попарно несовместных событий получим формулу Бернули

Pn(m)=n!/m!(n-m)!

Биноминальное распределение

Случайный эксперимент состоит в том, что осуществляется n независимых испытаний, в каждом из которых событие А может появиться или не появиться, причем вероят-ть наступления события А во всех испытаниях постоянна и равна р. Вероят-ть не наступления события А или наступления противоположно событию 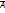: q =1- p .

В качестве дискретной случайной величины будем рассматривать число появлений события А в этих испытаниях. Необходиммо найти закон распределения дискретной СВ. События А в испытаниях может либо не наступить, либо наступить 1 раз, 2 раза или n раз. Таким образом возможное значение х может записываться так

х₁=0

х₂=1

х₃=2

……..

х_n₊₁=n

Вероят-ть можно найти с помощью формулы Бернулли

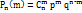, где n=1,2,…,n и m=1,2,…,m

Данная формула считается аналитическим выражением закона распределения дискретной СВ Х. Ф-ция распределения вероят-тей рассматриваемой СВ: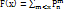

Распределение степени вероят-ти, которая определяется формулой Бернулли, называется биноминальным распределением. Биноминальный закон записывается так:

х	n	n-1	n-2	…	m
р	np	np^n-1q	p^n-2q²	…	mp

14. Распределение Пуассона . Для задач,в кот.число n независимых испытаний велико,а вероятность p наступления данного события А при каждом отдельном испытании мала,то искомые вероятности P_n(m) того,что в серии из n испытаний событие А наступит m раз могут быть вычислены с практически достаточной степенью точности по осимптотической формуле Пуассона: 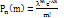Эта формула характеризует закон распределения Пуассона.Функция распределения вероятностей этой случайной величины имеет вид: 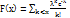Искомые вероятности можно вычислить с помощью специальных таблиц при известных m и λ.

15.Простейший поток событий. Поток событий – последовательность событий, кот. наступают в случайные заранее неизвестные моменты. Н-р, поступление вызовов на пункт неотложной скорой помощи. К основным св-вам, кот.хар-ют поток событий, относятся свойства стационарности, отсутствие последствий и ординарности. Свойство стационарности потока событий проявляется в том, что вероятность наступления m-событий на любом отрезке времени зависит только от числа m и от длительности его отсчета и не зависит от начала отсчета. При условии, что различные промежутки времени являются непересекающимися. Свойство отсутствия последствия проявляется в том, что вероятность наступления n-событий на любом отрезке времени не зависит от того, наступили или нет события в момент времени, кот. предшествуют началу рассматриваемого временного отрезка. Таким образом, если поток событий обладает свойством отсутствия последствия, то появление какого-либо числа событий в различные непересекающиеся отрезки времени считаются взаимно-независимыми. Свойство ординарности потока событий проявляется в том, что наступление 2-х и более событий за малый отрезок времени практически невозможно, т.е. вероятность наступления более 1-го события за малый отрезок времени, пренебрежимо мало, по сравнению с вероятностью наступления только 1-го события. Т.о. если поток событий обладает свойством ординарности, то за бесконечно малый отрезок времени может появиться не более 1-го события. Поток событий, кот. обладает св-вом стационарности, отсутствие последствий и ординарности наз.простейшим или Пуассоновским потоком. Интенсивность потока λ – это среднее число событий, кот. наступает в единицу времени. При заданной постоянной интенсивности потока λ,вероятность появления m-событий простейшего потока за временной отрезок длит.t можно рассчитать по формуле Пуассона: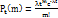

16.Мат.ожидание дискретной случайной величины. М(х) мат.ожидание дискретной случайной величины х, принимает значение х₁,х₂,…,х_n с вероятностями соотв. p₁, p₂,…,p_n наз.сумма произведений всех ее возможных n-значений на их вероятности.

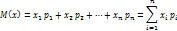
Математическое ожидание дискретной случайной величины х явл. неслучайной постоянной величиной. Если число возможных значений дискретной случайной величины конечно, то предполагается, что ряд сходится абсолютно.Пример: случайная величина х задана следующим законом распределения: х 4 6 9

P 0.5 0.3 0.2

Математическое ожидание числа появления событий в одном испытании равно вероятности этого события.

Теорема: математическое ожидание прим.равно среднему арифметическому наблюдаемых значений и случ.величины.

17.Свойство мат.ожидания дискретной случайной величины. 1.Мат.ожидание постоянной величины k=самой постоянной: M(k)=k; 2.Постоянный множитель можно выносить за знак мат.ожидания:M(kx)=kM(k); 3.Мат.ожидание-произведение нескольких попарно независимых случ.величин=произведению их мат.ожиданий. M(kyz)=M[(xy)z]= M(xy)M(z)=M(x)M(y)M(z)

4.Мат.ожидание-сумма 2-х случайных величин-сумме их мат.ожидания. M(x+y)=M(x)+M(y).Следствие:мат.ожидание суммы нескольких случ.величин. M(x+y+z)=M[(x+y)+z]=M(x+y)+M(z)=M(x)+M(y)+M(z).Следствие:мат.ожидание суммы нескольких случайных величин: M(x+y+z)=M[(x+y)+z]=M(x+y)+M(z)=M(x)+M(y)+M(z).

18.Дисперсия дискретной случайной величины. Понятие дисперсии случ.величины вводится для характеристики отклонения данной величины от ее среднего значения.Для этого рассм.понятие отклонения.Пусть х-случ.величина и М(х)-ее мат.ожидание. Отклонением наз.разность между случ.величиной х и ее мат.ожиданием.Теорема: мат.ожидание отклонения=0; M[x-M(x)]=0. Дисперсией или рассеянием дискретной случ.величины х наз.мат.ожидание квадрата отклонения случ.величины от ее мат.ожидания. D(x)=M(x-M(x))². Дисперсия случ.величины также имеет закон распределения.Пусть случ.величина х задана законом распределения

x	x₁	x₂	x₃	…	x_n
P	p₁	p₂	p₃	…	p_n

В этом случае дисперсия распределена по след.закону:

(x-M(x))²	(x₁-M(x))²	(x₂-M(x))²	…	(x_n-M(x))²
p	p₁	p₂	…	p_n

По закону распределения квадрата отклонения можно непосредственно рассчитать значение дисперсии

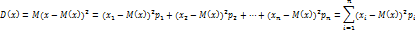
Теорема: дисперсия равна разности между между мат.ожиданием квадрата случ.величины х и квадратом ее мат.ожидания, т.е. D(x)=M(x)²-(M(x))².

Пример: случ.величина х задана законом распределения. Х 3 2 9 Найти дисперсию. М(х)=3*0.4+2*0.4+9*0.2=3.8

Р 0.4 0.4 0.2 М(х)²=9*0.4+4*0.4+81*0.2=21.4

D(x)=21,4-(3,8)²=6.96

Дата добавления: 2020-01-07; просмотров: 115; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 4 5 6 7 Следующая ⇒

Мы поможем в написании ваших работ!