Функция одного случайного аргумента и её распределения

⇐ ПредыдущаяСтр 6 из 7Следующая ⇒

Y наз-ся ф-ции случайного аргумента х в том случае, если каждому возможному значению СВ Х соответствует одно возможное значение СВ Y :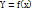

Необходимо найти распределение ф-ции Y по известному распределению аргумента Х. Рассмотрим несколько решений данной задачи: пусть аргумент Х – дискретная СВ

Если различным возможным значением аргумента Х соответствует различное возможное значение ф-ции Y, то вероят-ти соответствующих значений Х и Y равны между собой. Другими словами возможное значение Y находят из равенства 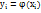, где 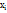- возможное значение Х. Вероят-ть возможного знаячения Yнаходят из равенства .

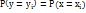Если различным возможным значениям Х соответствуют значения Y. Среди которых есть одинаковые значения, то вероят-ти повторяющихся значения Y необходимо суммировать. Другими словами вероят-ть повторяющегося значения Y равна сумме вероят-тей тех возможных значений Х, при которых Y принимает одно и тоже значение.

Пусть величина Х – НСВ в том случае, если ф-ция 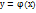является дифференцируемой в строго возрастающей или строго убывающей ф-цией, то дифференцируемая ф-ция q ( y ) СВ Y определяется равенством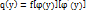

Математ.ожидание, функции одного аргумента

Пусть задана ф-ция 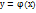случайного аргумента Х. Задача состоит в нахождении М(Y) при известном законе распределения аргумента Х. 2 способа:

Аргумент Х задан как дискретная СВ с возможными значениями х₁,х₂, …, х_n. Вероят-ти данных возможных значений соответственно равны р₁,р₂, …, р_n. СВ Y также является дискретной величиной с возможными значениями

, , …,

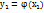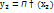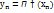
Если СВ Х приняло возможное значение х_i => СВ Y примент значение 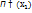. Тогда вероят-ти возможных значения СВ Y также равны р₁,р₂, …, р_n. Таким образом матем.ожидание ф-ции 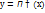можно найти по формуле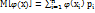

1. Аргумент Х является НСВ, которая задана дифферен.ф-цией 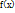. В данном случае матем.ожидание 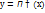может быть рассчитано двумя способами:

1) Можно рассчитать дифферен.ф-цию q ( y ) случайной величины Y, а затем применить формулу: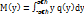

2) Если расчет дифферен.ф-ции q ( y ) является достаточно трудоемким, то матем.ожидание ф-ции 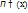можно найти по формуле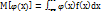

Если возможные значения СВ Х принадлежат интервалу (a;b), то матем.ожидание находят по формуле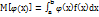

38. Функция двух случайных величин.Распределение суммы независимых слагаемых.

Если каждой паре возможных значений случайных величин Х и Y соответ-ствует одно возможное значение случайной величины Z, то Z называют функцией двух случайных аргументов X и Y : Z = φ(X , Y).

Рассмотрим в качестве такой функции сумму Х + Y. В некоторых случаях можно найти ее закон распределения, зная законы распределения слагаемых.

1) Если X и Y – дискретные независимые случайные величины, то для определения закона распределения Z = Х + Y нужно найти все возможные значения Z и соответствующие им вероятности.

2) Если X и Y – непрерывные независимые случайные величины, то, если плотность вероятно-сти хотя бы одного из аргументов задана на (-∞, ∞) одной формулой, то плотность суммы g(z) можно найти по формулам

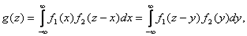
где f₁(x), f₂(y) – плотности распределения слагаемых. Если возможные значения аргументов неотрицательны, то

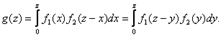Замечание. Плотность распределения суммы двух независимых случайных величин называют композицией.

Дата добавления: 2020-01-07; просмотров: 185; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 4 567 Следующая ⇒

Мы поможем в написании ваших работ!