Свойство дифферен.функции распределения вероят-тей

⇐ ПредыдущаяСтр 5 из 7Следующая ⇒

1. Дифферен.ф-ция неотрицательна f(x) 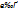0. Интегральная ф-ция есть неубывающая ф-ция => её производная. 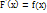есть ф-ция неотрицательная. График дифферен.функции называется кривой распределения.

2. Несобственный интергал от дифферен.функции в пределах от :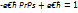

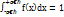
Доказательство: Несобственный интергал – это выражение вероят-ти события состоящего в том, что СВ х примет значение принадлежащее интервалу 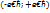, достоверное событие р=1. В том случае если все значения СВ х находятся в пределах интервала (a;b)

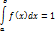
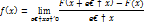
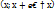=> предел отношения вероят-ти того. Что НСВ х примет значение а интервале 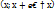к длине этого интервала. 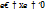равен значению интервал.ф-ции в точке Х. Значение 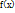в точке Х определяется как плотность вероят-ти в данной точке, те.е дифферен.ф-ция 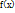определяет плотность распределения вероят-ти для точки Х.

Условные характеристики НСВ

Пусть х – это НСВ, которая задана дифферен.ф-цией 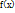. Предположим, что все возможные значения величины х принадлежат отрезку [a;b]. Разобьем этот отрезок на n частей, длины которых 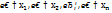и выделим в каждой из них произвольную точку 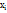, где i=1,2,3,…,n. Для того чтобы дать определение матем.ожиданию НСВ, составим сумму произведений возможных значений 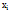на вероят-ти их попадания в интервал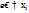

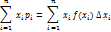
Так как произведение 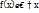приближенно равно вероят-ти попадания х в интервал 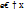. В результате перехода к пределу при условии, что длина наибольшего из полученных отрезков стремится к 0, получим открытый интеграл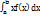

Матем.ожидание НСВ Х, чьи возможные значения принадлежат отрезку [a;b] – это число равное определенному интегралу вида 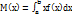. В том случае если возможные значения НСВ Х принадлежат всей оси Х, то 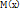будет равно интегралу 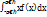. Последнее справедливо при условии, что несобственный интеграл сходится абсолютно, т.е. существует интеграл вида

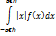
Если данное условие не выполняется, то значение интеграла независимо от скорости снижения нижнего предела к 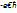, а верхнего – к 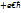по отдельности.

Дисперсия НСВ Х – это матем.ожидание квадрата её отклонения в том случае, если возможное значение НСВ Х принадлежит [a;b], то дисперсия определяется как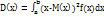

Если возможное значение НСВ Х принадлежит всей оси ОХ, то дисперсия равна

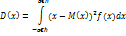
Среднее квадратическое отклонение НСВ Х – это корень квадратный из дисперсии данной величины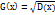

Те свойства матем.ожидания и дисперсии, которые были определены для дискретных случайных велични, справедливы и для НСВ Х.

Нормальное распределение

Нормальное распределение вероят-ти НСВ описывается дифференциальной функцией вида

f(x)=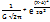

Данная ф-ция задается 2 параметрами a и G, т.е. достаточно определить эти параметры, чтобы задать нормал. Распределение. Параметр а в этом случае понимается как матем. ожидание, а параметр G – как среднее квадратическое отклонение нормал. распределения.

Рассмотрим параметр а дифферен. Ф-ции нормал.распределения вероят-ти. Матем.ожидание нормал. распределения НСВ находится по формуле:

M(x) =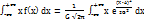

Введем новую переменную 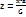; zG + a = x , тогда dx = G dz. С учетом новой переменной z матем.ожидание можно записать в виде:

M(x) =

1-ое слагаемое = 0; 2-ое слагаемое = a . Таким образом матем.ожидание нормал.распределения равно параметру а.

Рассмотрим параметр G дифферен.ф-ции нормал.распределния вероят-ти. Дисперсия нормал.распределния НСВ Х с учетом того что М(х)=а имеет вид:

D(x) =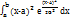

Вновь используем переменную z,на основе к-рой получим след. равенство: zG+a=x ; dx=Gdz. С учетом новой переменной z дисперсию можно записать в след.виде:

D(x) =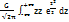

В результате интегрирования данного выражения по частям получим D(x) = 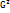, следовательно G(x) = 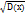. Таким образом среднее квадратическое отклонение нормал.распределения равно параметру G. Если нормал.распределения определяется М(х) = 0 и G(x) = 1, то такое распределение называется нормальным, и дифферен.ф-ция нормал.распределения имеет вид:

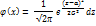
Вероят-ть того, что Х примет значение принадлежащее интервалу 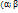), находиться по формуле: , где а – мат.ожидание, G – среднее квадратическое откл-е

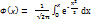- функция Лапласа

Нормальная кривая

Дифферен.ф-ция нормал.распределенной НСВ имеет вид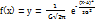

График дифферен.ф-ция нормал.распределения вероят-ти наз-ся нормал.кривой или кривой Гаусса. Исследуем дифферен.ф-ция нормал.распределения с помощью метода дифферен. Исчисления:

Данная ф-ция определена на всей оси ОХ

Нормал.кривая расположена над осью ОХ, т.к. при всех значениях х ф-ция принимает положительные значения

Предел ф-ции при неограниченном возрастании х равен 0

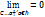- это означает, что ось ОХ явл-ся горизонтальной асимптотой.

Найдем 1-ую производную ф-ции для исследования её на экстремум

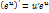
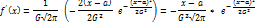
При х=а, у’=0; при x< a , y’>0 ; при x> a , y’<0.

Отсюда следует, что при х= а ф-ция принимает максимальное значение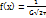

График симметричен относительно прямой х=a. Находим 2-ую производную ф-ции для исследования её на точке перегиба

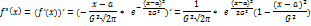
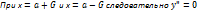
А при переходе через эти точки он меняет знак. В обеих этих точках значение ф-ции равно 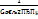следовательно (a-G; 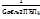) и (a+G; 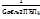) явл-ся точками перегиба

При а=0 и G=0

Изменение величины матем.ожидания, т.е величины параметра а дифферен.ф-ции нормал.распределения не меняет формы, а приводит её к сдвигу вдоль оси абцисс. При увеличении а сдвиг вправо, при уменьшении а сдвиг влево

При возрастании G максимальная ордината нормал.кривой убывает, а сама кривая становиться более пологой, те.е сжимается к оси ОХ. При уменьшении нормал.кривая становиться более островершинной и растягивается.

Площадь фигуры ограниченной нормал.кривой и осью ОХ при любых значениях параметров а и G будет равно 1.

Правила 3х сигм

Пусть НСВ Х задана дифферен.ф-цией f(x), тогда по теореме вероят-ти того, что х примет значение принадлежащее интервалу 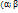), будет равна

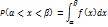
Пусть НСВ Х подчиняется нормал.закону распределения. В этом случае вероят-ть того, что Х примет значение принадлежащее интервалу 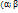), равна

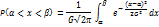
Можно воспользоваться готовыми таблицами, приведя данную формулу к виду

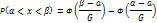
Определим вероят-ть что отклонение нормал.распреленной величины Х по абсолютной величине будет меньше заданного положительного числа а, т.е. найдем вероят-ть осуществления вероят-ти

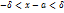
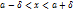
На основании выше приведенной формулы получим

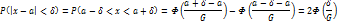
В этом случае если параметр а равен 0, мы имеем

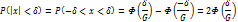
Зададим параметру 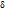значение равное Gt . получим 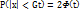. Если 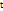=3, то 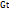=3 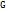, тогда вероят-ть того, что отклонение нормал.распределенной СВ Х по абсолютной величине будет равно 2Ф(3). Данная вероят-ть выражается в существование 3^х G . Если НСВ подчиняется нормал.закону распределения, то абсолютная величина её отклонения от матем.ожидания не превосходит утроенного вреднего квадратического отклонения.

Теорема Ляпунова

При проведении какого-либо статистического исследования, сопровождающегося сбором данных об изучаемом количественном признаке, всегда сталкиваются с проблемой ошибки данных. Проблема может быть вызвана как несовершенства методов и инструментов, используемых при проведении стат. исследования, так и заранее непредусмотренных факторов. Ошибки делятся на систематические и случайные.

Систематические ошибки – ошибки, вызванные несовершенством методов и инструментов, применяемых при проведении исследования. Теоретически все эти ошибки могут быть исключены. Случайные ошибки – ошибки, которые вызваны под воздействием целой совокупности случайных факторов. Результатом совместного действия всех случайных факторов является суммарная случайная ошибка, которую необходимо оценить. Предположим, что осуществляется серия наблюдений, как CВ Х. Ошибки, которые возникают в ходе произведения наблюдений данной СВ, формируются по воздействием многих незавершенных факторов х₁,х₂, …, х_n_.В этом случае ошибка 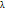, возникающая при наблюдении СВ Х, может быть охарактеризована след.образом 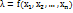, где f – законность образованных ошибок.

В случае если ф-ция f удовлетворяет условию дифферентности по совокупности всех переменных, тогда ф-ция f может быть предназначена для формулы Пейлора

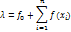
1-ое линейное приближенное значение ошибки 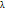является суммарной независимой СВ :

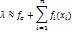
Ошибка наблюдения 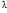является СВ, поэтому для наиболее точной характеристики данной величины необходимо знать закон распределения вероят-тей СВ 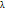. Решение поставленной проблемы было найдено русским математиком Ляпуновым, который открыл централ.предельную теорему теории вероят-тей.

Следствие из теоремы: если СВ Х – сумма очень большого числа попарно-независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то СВ Х подлежит закону распределения, которых близок к нормал.закону распределения вероят-тей СВ.

Ассиметрия и эксцесс

Теоретическим распределением является распределение вероят-тей случайных величин. Подобное распределение изучается в теории вероят-ти. В том случае если изучаемое распределение вероят-тей отличается от нормал. распределения, то возникает необходимость количественной оценки этого различия. Данное оценивание осуществляется с помощью спец. Характеристик (в частности показатели ассиметрии и эксцесса).

Если СВ подчиняется нормал.закону распределения, то в данном случае показатели ассиметрии и эксцесса равны 0. Если ассиметрия и эксцесс имеют небольшие значения, можно предположить, что изучаемое распределение вероят-ти СВ близок к 0. Если же напротив ассиметрия и эксцесс имеют большие значения, то это является признаком значительного отклонения изучаемой величины от нормал.распределения.

Для оценки ассиметрии используется понятие симметрического распределения, график которого симметричен относительно прямой х=М(х). В данном случае каждый централ.момент нечетного порядка равен 0, т.е.

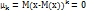, когда k=1,3,5…

Для несимметрических распределений централ.моменты нечетного порядка отличны от 0. Следовательно любой из централ.моментов может служить для оценки ассиметрии, кроме централ.момента первого порядка, который равен 0 для любого распределения

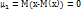. Оценка ассиметрии осуществляется с помощью централ.момента 3-го порядка. Однако величина данного показателя зависит от единиц, в которых изучается СВ.

Для устранения этого недостатка централ.момент 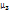делят на показатель G в кубе, сто позволяет получить безразмерную характеристику.

Ассиметрия теоретического распределения – отношение централ.момента 3-го порядка к кубу среднего квадратического отклонения 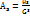. Показатель ассиметрии является положительным, если данная часть кривой распределния на графике расположена справа от М(х) и отрицательным – если слева от М(х).

Показатель эксцесса применяется для оценки большого или меньшего подъема кривой теоретического распределения по сравнению с нормал.кривой. Эксцесс теоретического распределения – это характеристика, которая рассчитывается по формуле 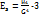. Если СВ подчиняется нормал.закону распределения, то 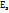=0 следовательно 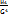= 3. Если показатель 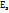отличен от 0, то кривая этого распределения отличается от нормал.кривой.

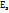> 0 => кривая имеет более высокую и острую вершину, чем нормал.кривая.

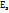< 0 => кривая распределения имеет более низкую и плоскую вершину, чем нормал.кривая. Это при условии, что нормальное и теоретическое распределения имеют одинаковые математ.ожидание и дисперсию.

Дата добавления: 2020-01-07; просмотров: 110; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 456 7 Следующая ⇒

Мы поможем в написании ваших работ!