Тема 2.6. Понятие о касательных напряжениях
При изгибе. Линейные и угловые перемещения
При изгибе, их определение
Иметь представление о касательных напряжениях при изгибе, об упругой линии балки, о деформациях при изгибе и методах определения линейных и угловых перемещений.
Знать один из методов определения линейных и угловых перемещений.
Поперечный изгиб. Внутренние силовые факторы.
Напряжения
Рассмотрим изгиб балки, защемленной справа и нагруженной сосредоточенной силой F (рис. 33.1).
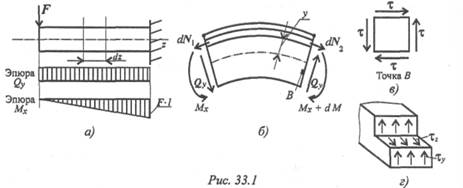
В поперечном сечении возникает изгибающий момент, меняющийся по длине балки, и постоянная поперечная сила Q .
Рассмотрим участок балки длиной dz (рис. 33.1b).
Изгибающий момент, как известно, является равнодействующим элементарных моментов, возникающих в результате действия продольных сил упругости. Связь между нормальными напряжениями в точках поперечного сечения и изгибающим моментом уже рассматривал ась:
Тема 2.6. Понятие о касательных напряжениях при изгибе 271
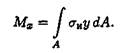
Поперечная сила представляет собой равнодействующую касательных сил упругости, возникающих в поперечных сечениях (рис. 33.1в), и связана с касательными напряжениями зависимостью
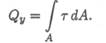
В силу парности касательных напряжений в продольных сечениях балок, параллельных нейтральному слою, возникают такие же по величине касательные напряжения (рис. 33.1г).
|
|
|
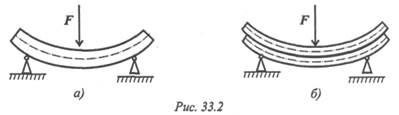
Появление касательных напряжений в продольных слоях балок подтверждается следующим опытом. Рассмотрим поперечный изгиб двух балок, одна — цельная, другая — составленная из нескольких положенных друг на друга слоев (рис. 33.2). Цельная балка изогнется (рис. 33.2а), брусья второй балки сдвинутся (рис. 33.26). Каждый из брусьев деформируется независимо. В цельной балке сдвигу слоев препятствуют возникающие касательные напряжения.
На поверхности касательные напряжения равны нулю.
Формула для расчета касательных напряжений для балки квадратного сечения была получена в 1855 году русским инженером Д. И. Журавским,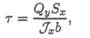 
где Qy — поперечная сила в сечении; Sx — статический момент отсеченной части относительно оси х, Sx = Аoтсyc, Аoтс — площадь поперечного сечения отсеченной части (рис. 33.3); Jx — момент инерции сечения; b— ширина балки.
272 Лекция 33
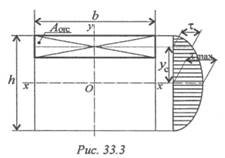Наибольшее значение касательного напряжения достигается на нейтральной оси: 
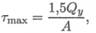А — площадь сечения.
|
|
|
Максимальное напряжение при поперечном изгибе в полтора раза больше среднего значения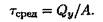 
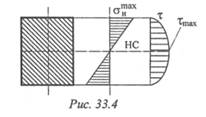Обнаруживается, что максимальные нормальные напряжения в сечении не совпадают с максимальными касательными (рис. 33.4).
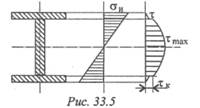
Для длинных балок расчет проводят только по нормальным напряжениям, т. к. касательные здесь не значительны. Для коротких балок, нагруженных значительными поперечными силами вблизи опор, проводят расчет по касательным напряжениям. Однако для тонкостенных профилей (двутавр, швеллер) необходимо проверять прочность балки в точках, где полка сочленяется со стенкой. Здесь и нормальные, и касательные напряжения значительны (рис. 33.5).
Дата добавления: 2019-09-13; просмотров: 421; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!