Определение внутренних силовых факторов

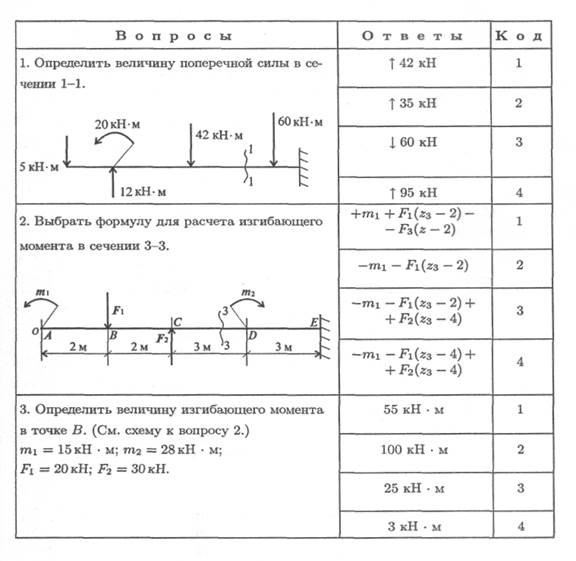
254                                                                               Лекция 30

 

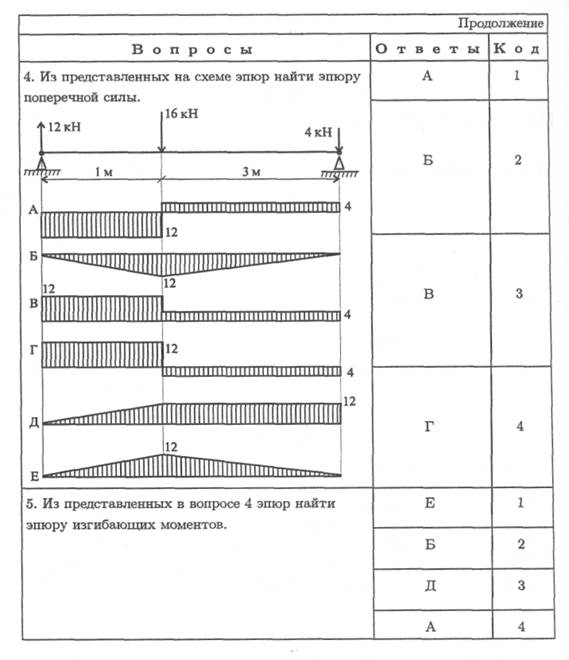
                                                                    Тема 2.6. Изгиб                                                                255

ЛЕКЦИЯ 31

Тема 2.6.    Изгиб.

Построение эпюр поперечных сил и изгибающих

Моментов. Приложены сосредоточенные и распределенные

Нагрузки

Знать дифференциальные зависимости между интенсивно­стью распределенной нагрузки, поперечной силой и изгибающим моментом, основные правила построения эпюр.

Уметь строить эпюры поперечной силы и изгибающего момен­та в случае приложения сосредоточенных и распределенных нагру­зок.

Примеры решения задач

Пример 1. Одноопорная балка нагружена сосредоточенными силами и распределенной нагрузкой (рис. 31.1). Построить эпюры поперечных сил и изгибающих моментов.

Решение

Задачу решаем с помощью составления уравнений поперечных сил и изгибающих моментов в поперечных сечениях балки.

При проверке эпюр используем дифференциальные зависимости между интенсивностью распределенной нагрузки, поперечной силой и изгибающим моментом:

1. Производная от поперечной силы по длине балки равна интенсивности распределенной нагрузки

            

2. Производная изгибающего момента по длине балки равна по­
перечной силе

           

256                                                      Лекция 31

 

        

Рассмотрим участок 1, сечение 1.

Поперечная сила Q1 = — F1 =—15 кН.

По принятому правилу знаков поперечная сила отрицательна и постоянна на этом участке.

Изгибающий момент М_Х1 = — F1z1.

0 ≤ z1 ≤ 4м:  М_А = 0; М _B = -15 • 4 = -60кН • м.

Рассмотрим участок 2, сечение 2.

Поперечная сила Q2 = — F1— q (z2 - 4).

4 м ≤ z ₂ ≤ 8 м: Q_B = - F1 = -15 кН; Q с^{слев a} = -39 кН.

Поперечная сила изменяется по линейному закону.

Изгибающий момент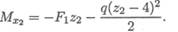  

 4 м ≤ z ₂ ≤ 8 м:

                                                                       Тема 2.6. Изгиб                                                             257

при Z2 = 4 м изгибающий момент Мв = —60 кН • м. В точке В нет внешнего момента, поэтому изгибающий момент слева и справа от точки В одинаков. В этом случае рассчитывать его дважды не следует;

Рассмотрим участок 3, сечение 3.

В точке С приложена внешняя сила F2.На эпюре должен быть скачок, равный приложенной силе; на эпюре моментов должен быть излом.

Поперечная сила на участке 3: Q3 = - F1- q (z3 - 4)-F2;

при z₃ = 8м Q с^справа = -15 - 6 • 4 - 10 = -49кН;

точка С: Q с^слева = 39 кН; Q с^справа = 49 кН;

при z₃ = 10м Q_D = -15-6∙6- 10 = -61кН.

Поперечная сила изменяется по линейному закону.

Изгибающий момент

                                

8 м ≤ z ₃ ≤ 10 м:

На участках 2 и 3 эпюра изгибающих моментов ограничена ква­дратичной параболой.

По полученным результатам, учитывая дифференциальные за­висимости между поперечной силой и изгибающим моментом, стро­им эпюры Q и М_х. На втором и третьем участках поперечная сила не имеет нулевых значений, поэтому на эпюре моментов нет экс­тремумов.

Основные правила построения эпюр в случае приложения распределенной нагрузки. Контроль правильности решений

1. Для участка балки с равномерно распределенной нагрузкой поперечная сила Q изменяется по линейному закону, эпюра ограни­чена наклонной прямой. Изгибающий момент изменяется по квадра­тичному закону, эпюра М_х ограничена параболой второго порядка.

2. В сечении, где эпюра Q переходит через ноль (наклонная ли­ния пересекает ось абсцисс), изгибающий момент экстремален: ка­сательная к эпюре М_х в этом месте параллельна оси абсцисс.

9- 8060 Олофинская

258                                                                                                                   Лекция 31

3. Параболическая и прямолинейная части эпюры моментов там,
где кончается или начинается распределенная нагрузка, сопрягаются плавно, без излома, если в соответствующем сечении к балке не
приложена сосредоточенная сила.

4. Если распределенная нагрузка направлена вниз, то эпюра мо­мента очерчена параболой, обращенной выпуклостью вверх.

5. Из теоремы Журавского следует:

— если на участке Q > 0, М_И растет;

— если на участке Q < 0, М_Иубывает;

— если на участке Q = 0, изгибающий момент постоянен (чи­стый изгиб);

— если в точке Q = 0, изгибающий момент достигает экстремального значения ( Ми^min или Ми^max ).

Пример 2. Расчет двухопорной балки. Двухопорная балка на­гружена равномерно распределенной нагрузкой (рис. 31.2).

Решение

При определении реакций в опоре равномерно распределенную нагрузку можно   заранее  заменить  равнодействующей  сосредоточен­ной  силой:  G = q l ; q = 4кН/м;   G = 4 • 6 = 24кН (рис. 31.2).

При построении эпюр поперечных сил и изгибающих моментов распределенная нагрузка учитывается постепенно.

Расчет балки можно провести по характерным точкам, при этом необходимо знать правила построения эпюр, перечисленные выше.

              

Определяем реакции в опорах балки.

        

                                                                                     Тема 2.6. Изгиб                                                                 259

 

Построение эпюр

Анализируем схему балки.

Рассмотрим участок 1 до сечения 1.

В опоре А действует сосредоточенная сила Ra = 7,2 кН. На участке 1 поперечная сила остается постоянной: Q 1 = Ra = 7,2 кН (рис. 31.3).

         

Изгибающий момент в точке А равен нулю, т. к. здесь нет мо­мента внешней пары сил: Ма = 0.

Момент в точке С (граница участка, z — 4м) Мс = Ra • 4; М_с = 7,2 -4 = 28,8кН • м.

Эпюра очерчивается прямой линией, наклонной к оси Oz (рис. 31.3).

260                                                                  Лекция 31

Рассмотрим участок 2 (рис. 31.3). Здесь действует распределен­ная нагрузка интенсивностью q = 4кН/м. При перемещении вдоль оси балки направо распределенная нагрузка суммируется. Эпюра Q2— прямая линия, наклонная к оси Oz . Распределенная нагруз­ка направлена вниз (см. Основные правила построения эпюр, п. 4), здесь эпюра изгибающего момента очерчена параболой, обращенной выпуклостью вверх.

Реакция в опоре Ra и распределенная нагрузка направлены в разные стороны. Следовательно, возможна точка, в которой, по пра­вилу 2, Q2 = 0, а изгибающий момент экстремален.

Для построения эпюры моментов необходимо составить уравне­ние поперечной силы на участке 2 и приравнять величину попереч­ной силы нулю. Из уравнения можно определить координату точки, в которой изгибающий момент экстремален.

Проводим необходимые расчеты, определяем величины попереч­ных сил и изгибающих моментов в характерных точках.

Рассмотрим участок 2, сечение 2 (рис. 31.3).

Уравнение поперечной силы Q2 = Ra — q ( z2— 4) = 0.

Откуда: 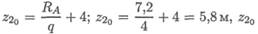  — координата

точки, где изгибающий момент экстремален, т. к. Q2 = 0.

  Уравнение момента на участке 2:

Максимальное значение изгибающего момента на участке 2                                    

                      

Значения    поперечной    силы    и    изгибающего    момента    в    точке  В : Q_B = R_B = 16,8 кН; М_В = 0.

Строим эпюру поперечной силы. Первый участок — прямая ли­ния, параллельная оси Oz . В точке С эпюра становится наклонной. Строим эпюру изгибающих моментов (рис. 31.3).

Участок 1 эпюра — прямая линия; Ма = 0; Мс — 28,8 кН • м.

Участок 2 эпюра — парабола с    экстремумом    в    точке  z = 5,8 м;

                                                                         Тема 2.6. Изгиб                                                           261

          

Контрольные вопросы и задания

1. Если эпюра поперечной силы ограничена наклонной прямой, как выглядит эпюра изгибающего момента?

2. Как определить положение экстремального значения изгиба­ющего момента при действии распределенной нагрузки на участке балки?

3. Распределенная нагрузка направлена вверх. Как выглядит парабола, очерчивающая эпюру изгибающих моментов вдоль оси бруса?

4. Определите координату z , в которой поперечная сила равна нулю (рис. 31.4).

 

 

5. Определите величину изгибающего момента в точке С (z = 5 м), используя схему рис. 31.4.

262                                                                                 Лекция 32

ЛЕКЦИЯ 32

Тема 2.6. Изгиб.

---

Дата добавления: 2019-09-13; просмотров: 780; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!