Рациональные сечения при изгибе

Определим рациональные сечения при изгибе, для этого срав­ним моменты сопротивления простейших сечений.

Осевой момент инерции прямоугольника (рис. 32.4, вывод формулы в лекции 25) равен 

                                                

Осевой момент сопротивления прямо­угольника

Сравним сопротивление изгибу двух прямоугольных сечений (рис. 32.5).

             

Вариант на рис. 32.5b обладает большим сопротивлением изги­бу при прочих равных условиях.

Осевой момент инерции круга (рис. 32.6) равен

                

Все необходимые расчетные данные (площади, моменты инер­ции и сопротивления) стандартных сечений приводятся в таблицах стандартов (Приложение 1).

266                                                                          Лекция 32

Для материалов, одинаково работающих на растяжение и сжа­тие, выбирают сечения, симметричные относительно оси, вокруг ко­торой совершается изгиб (рис. 32.7).

Пример

Сравним моменты сопротивления двух сечений одинаковой пло­щади: двутавра (рис. 32.7г) и круга (рис. 32.7а).

Двутавр № 10 имеет площадь 12 см², осевой момент инерции 198 см⁴, момент сопротивления 39,7 см³.

Сопротивление изгибу у двутавровой балки в шесть раз выше, чем у балки круглого сечения.

Из этого примера можно сделать вывод: сечения прямо­угольные, квадратные, круглые и ромбовидные нерациональны (рис. 32.7а, б).

           

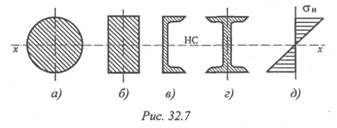
Для материалов, обладающих разной прочностью при растяже­нии и сжатии (хрупкие материалы обладают значительно большей прочностью на сжатие, чем на растяжение), выбирают асимметрич­ные сечения тавр, рельс и др.

Расчет на прочность при изгибе

Рассчитать на прочность — это значит определить напряжение и сравнить его с допустимым.

Условие прочности при изгибе:

        

                                                                  Тема 2.6. Изгиб                                                            267

где [σ_и] — допускаемое напряжение.

По этому неравенству проводят проверочные расчеты после окончания конструирования балки.

Для балок из хрупких материалов расчеты ведут по растянутой и сжатой зоне одновременно (рис. 32.8).

              

При проектировочном расчете определя­ют потребные размеры поперечных сечений  балки или подбирают материал. Схема нагружения и действующие нагрузки известны.

По условию прочности можно определить нагрузочную способ­ность балки [М_и] = W_p[ σ ].

Примеры решения задач

Подобрать размеры сечения балки в виде двутавра. Известна схема нагружения балки (рис. 32.9), материал — сталь, допускаемое напряжение материала при изгибе [σ_р] = [σ_с] = 160 МПа.                         Решение

1. Для защемленной балки реакции в опоре определять не следует.

Проводим расчеты по характерным точкам. Раз­меры сечения подбираем из расчета по нормаль­ным напряжениям. Эпю­ру поперечных сил стро­ить необязательно.

Определяем моменты в характерных точках. М_А = 0; М _B = F 1·4; М _B = 20·4 = 80 кН·м.

В точке С приложен внешний момент пары, поэтому расчет про­водим для левого сечения (без момента) и для правого — с моментом  m. 

268                                                                                 Лекция 32

 

МС^лев = F1 • 6 - F ₂ • 2; МС^лев= 20 • 6 - 45 • 2 = 30 кНм.   Момент положительный.

Мс^прав = МС^лев+ m; Мс^прав= 30 + 25 = 55 кН·м.

Момент в заделке M d = F1 · 8 - F ₂ · 4 + т;

M_D = 20 · 8 - 45 · 4 + 25 = 5кНм.

Выбираем соответствующий масштаб по максимальному значе­нию изгибающего момента.

Опасное сечение — сечение балки, где действует максимальный момент. Подбираем размеры балки в опасном сечении по условию прочности

               

Основываясь на значении W_x = 500 см³ по таблице ГОСТ 8239-89 выбираем двутавр № 30а: момент сопротивления W_x = 518 см³; пло­щадь сечения А = 49,9 см³.

Для сравнения рассчитаем размеры балки квадратного сечения (рис. 32.10) при  том же моменте сопротивления сечения.

              

 

Сторона квадрата b ≥ ³√6 · 500 ≈ 14,5 см. Площадь сечения бал­ки А = b² = = 14,5² = 210,2см².

                                    

Балка квадратного сечения в 4 раза тяжелее.

        

Контрольные вопросы и задания

1. Напишите формулу для определения нормального напряже­ния при изгибе в любой точке поперечного сечения.

                                                                   Тема 2.6. Изгиб                                                                269

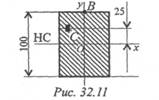
2. Нормальное напряжение в точке В поперечного сечения
120 МПа. Определите напряжение в точке С (рис. 32.11).

             

             

3. В каком случае (рис. 32.12) балка выдержит большую
нагрузку?

             

          

 

4. Напишите формулы для определения момента инерции и мо­мента сопротивления для прямоугольника. Что характеризуют эти величины? Укажите единицы измерения этих величин.

5. Напишите условие прочности при изгибе.

6. Определите изгибающий момент в точке В (рис. 32.13), ис­пользуя метод характерных точек.

 

 

7. Подберите размеры поперечного сечения балки в виде швел­лера. Максимальный изгибающий момент 15кНм; допускаемое на­пряжение материала балки 160 МПа.

270                                                                                      Лекция 33

         ЛЕКЦИЯ 33

---

Дата добавления: 2019-09-13; просмотров: 766; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!