Из точки А, удаленной от плоскости a на 12 см, проведена к этой плоскости наклонная АВ, равная 37 см. Найти проекцию наклонной АВ на плоскость a .
2. Из точки вне плоскости проведена к этой плоскости наклонная, равная 20 см, образующая с этой плоскостью угол 45 °. Найти расстояние от данной точки до плоскости.
Из центра круга радиуса 18 см восстановлен перпендикуляр к его плоскости. Найти расстояния от конца этого перпендикуляра до точек окружности, если длина перпендикуляра 80 см.
4. Из вершины D прямоугольника АВСD, стороны которого АВ = 9 см и ВС = 8 см, восстановлен к плоскости прямоугольника перпендикуляр DF = 12 см. Найти расстояния от точки F до вершин прямоугольника.
8. ДВУГРАННЫЙ УГОЛ. ЛИНЕЙНЫЙ УГОЛ ДВУГРАННОГО УГЛА
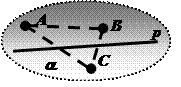 III4. Любая прямая р, лежащая в плоскости a, разбивает множество не принадлежащих ей точек этой плоскости на два непустых множества так, что любые две точки, принадлежащие разным множествам, разделены прямой р; любые две точки, принадлежащие одному и тому же множеству, не разделены прямой р.
III4. Любая прямая р, лежащая в плоскости a, разбивает множество не принадлежащих ей точек этой плоскости на два непустых множества так, что любые две точки, принадлежащие разным множествам, разделены прямой р; любые две точки, принадлежащие одному и тому же множеству, не разделены прямой р.
Множества, на которые прямая р разбивает множество не принадлежащих ей точек плоскости a , называются открытыми полуплоскостями с границей р.
Объединение открытой полуплоскости с её границей называется полуплоскостью.
Определение: Фигура, состоящая из двух лучей с общим началом и ограниченной ими части плоскости, называется углом.
Определение: Угол называется развёрнутым, если стороны угла образуют прямую.
Проведём аналогию между плоскостью и пространством.
 Рассмотрим фигуру, образованную двумя различными полуплоскостями с общей границей. Она делит пространство на две части.
Рассмотрим фигуру, образованную двумя различными полуплоскостями с общей границей. Она делит пространство на две части.
|
|
|
Определение: Фигура, состоящая из двух полуплоскостей с общей границей и ограниченной ими части пространства, называется двугранным углом.
Обозначение: 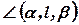
Определение: Двугранный угол называется развёрнутым, если его грани образуют плоскость.
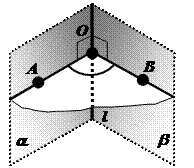 Определение: Угол, являющийся пересечением двугранного угла плоскостью, перпендикулярной его ребру, называется линейным углом двугранного угла.
Определение: Угол, являющийся пересечением двугранного угла плоскостью, перпендикулярной его ребру, называется линейным углом двугранного угла.
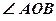 - линейный угол двугранного угла
- линейный угол двугранного угла 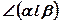
1. 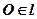
2. 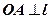
3. 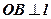
Замечание:
- Градусная мера двугранного угла – это градусная мера его линейного угла.
- В зависимости от линейного угла двугранный угол может быть острым, тупым, прямым, развёрнутым.
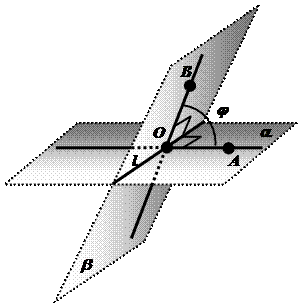 Рассмотрим две пересекающиеся плоскости:
Рассмотрим две пересекающиеся плоскости: 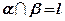 . Две пересекающиеся плоскости образуют четыре двугранных угла с общим ребром.
. Две пересекающиеся плоскости образуют четыре двугранных угла с общим ребром.
Определение: Углом между двумя пересекающимися плоскостями называется наименьший из двугранных углов, полученных при их пересечении.
Обозначение: 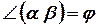 ;
; 
Замечание: 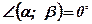 , если
, если 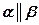
Определение: Две плоскости называются перпендикулярными, если угол между ними прямой.
9. 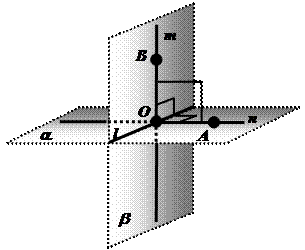 ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ ДВУХ ПЛОСКОСТЕЙ
ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ ДВУХ ПЛОСКОСТЕЙ
|
|
|
Теорема: Если плоскость проходит через перпендикуляр к другой плоскости, то эти плоскости перпендикулярны.
Дано: 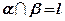 ;
; 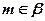 ;
; 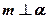
Доказать: 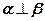
Упражнения:
Сторона ВС прямоугольника АВСD служит стороной треугольника ВСF, причём вершина F проектируется на DС. Назвать линейный угол двугранного угла, образованного плоскостями АВС и ВСF (Рис. 1.).
 | |||
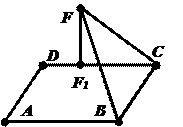 | |||
Рис. 1. Рис. 2.
Дано изображение равнобедренной трапеции АВСD и треугольника АВМ. Отрезок МС перпендикулярен плоскости АВС. Построить линейный угол двугранного угла, образованного плоскостями АВС и АВМ так, чтобы одна из его сторон проходила через точку М (Рис. 2.).
3. На грани двугранного угла, равного 45 °, дана точка, удалённая от ребра на 4 см. Найти расстояние от этой точки, до другой грани.
10. Упражнения по теме «Прямые и плоскости в пространстве»:
Стороны треугольника равны 20 см, 65 см, 75 см. Из вершины большего угла треугольника проведён к его плоскости перпендикуляр, равный 60 см. Найти расстояние от концов перпендикуляра до большей стороны треугольника.
2. Из точки, отстоящей от плоскости на расстоянии 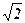 см, проведены две наклонные, образующие с плоскостью углы, равные
см, проведены две наклонные, образующие с плоскостью углы, равные 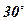 , а между собой – прямой угол. Найти расстояние между точками пересечения наклонных с плоскостью.
, а между собой – прямой угол. Найти расстояние между точками пересечения наклонных с плоскостью.
|
|
|
3. Сторона правильного треугольника равна 12 см. Точка М выбрана так, что отрезки, соединяющие точку М со всеми вершинами треугольника, образуют с его плоскостью углы 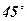 . Найти расстояние от точки М до вершин и сторон треугольника.
. Найти расстояние от точки М до вершин и сторон треугольника.
4. Двугранный угол между плоскостями треугольников АВС и DВС равен 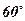 . Найти АD, если АВ = АС =5 см, ВС = 6 см, ВD = DС =
. Найти АD, если АВ = АС =5 см, ВС = 6 см, ВD = DС = 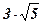 см.
см.
Контрольные вопросы по теме «Прямые и плоскости в пространстве»
Дата добавления: 2019-09-13; просмотров: 460; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
