Дан тетраэдр DАВ C. Точки М, N, Р являются серединами ребер DА, DВ, DС. Доказать, что плоскости МNР и АВС параллельны.
6. УГОЛ МЕЖДУ ПРЯМЫМИ
ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ ПРЯМОЙ И ПЛОСКОСТИ
УГОЛ МЕЖДУ ПРЯМЫМИ
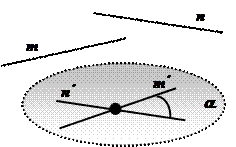
Определение: Углом между непараллельными прямыми т и п называется меньший из смежных углов, образованных пересекающимися прямыми т' и п', где т' || т , п' || п .
, 
, 
.
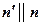Замечание: Угол между параллельными прямыми считается равным нулю.
Определение: Две прямые в пространстве называются перпендикулярными, если угол между ними равен 
.
Обозначение: 
Перпендикулярные прямые могут пересекаться и могут быть скрещивающимися.
Задача: Дан куб АВСDА1В1С1D1.
Найти: 
; 
; 
.
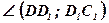Решение:
По признаку параллельности двух прямых:
и 
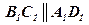, следовательно, 
. 
.
. 
, так как СDD1С1 является квадратом.
.
По признаку скрещивающихся прямых:
, следовательно, 
· 
.
, следовательно, 
.
.
Вывод: 
ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ ПРЯМОЙ И ПЛОСКОСТИ
 |
Определение: Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости.
Обозначение: 
Вывод: Через данную точку можно провести только одну прямую, перпендикулярную к данной плоскости.
Как проверить, перпендикулярна ли данная прямая к данной плоскости? Этот вопрос имеет практическое значение, например, при установке мачт, колонн зданий, которые нужно поставить прямо, т. е. перпендикулярно к той плоскости, на которую они ставятся. Оказывается, для этого нет необходимости проверять перпендикулярность данной прямой к любой прямой этой плоскости, как о том говорится в определении.
|
|
|
Рассмотрим признак перпендикулярности прямой и плоскости.
Теорема: Если прямая перпендикулярна к двум пересекающимся прямым, принадлежащим плоскости, то она перпендикулярна к этой плоскости.
Дано: 
, 
, 
, 
.
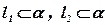Доказать: 
.
Вывод: Чтобы доказать, что данная прямая перпендикулярна данной плоскости, надо в этой плоскости найти две пересекающиеся прямые, которым данная прямая перпендикулярна.
Упражнения:
1. Сторона АВ правильного треугольника АВС лежит в плоскости a . Может ли быть перпендикулярна к этой плоскости:
A) ВС,
B) С D, где D – середина АВ?
2. Через точку О пересечения диагоналей квадрата, сторона которого равна а, проведена прямая ОК, перпендикулярная к плоскости квадрата. Найти расстояние от точки К до вершин квадрата, если ОК = b.
3. В треугольнике АВС дано: Ð С = 90 °, АС = 6 см, ВС = 8 см, СМ – медиана. Через вершину С проведена прямая СК, перпендикулярная к плоскости треугольника АВС, причем СК = 12 см. Найти КМ.
7. УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮ
ТЕОРЕМА О ТРЕХ ПЕРПЕНДИКУЛЯРАХ
ПОНЯТИЕ ПЕРПЕНДИКУЛЯРА И НАКЛОННОЙ К ПЛОСКОСТИ. СВОЙСТВА ПЕРПЕНДИКУЛЯРА И НАКЛОННЫХ, ОПУЩЕННЫХ НА ПЛОСКОСТЬ ИЗ ОДНОЙ ТОЧКИ
|
|
|
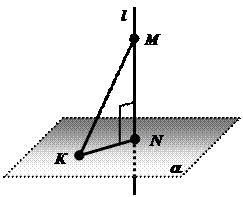Рассмотрим плоскость a и точку М, не принадлежащую этой плоскости. Проведем через точку М прямую l, перпендикулярную плоскости a. Прямая пересечет плоскость в точке N.
Отрезок МN называется перпендикуляром, проведенным из точки М к плоскости a, а точка N – основанием перпендикуляра.
Отметим в плоскости точку К, отличную от точки N, и проведем отрезок МК.
Отрезок МК называется наклонной, проведенной из точки М к плоскости a, а точка К – основанием наклонной.
Отрезок NК называется проекцией наклонной МК на плоскость a.
Определение: Проекцией наклонной на плоскость называется отрезок, соединяющий основание перпендикуляра с основанием наклонной, проведенных к плоскости из одной точки.
Обозначение: 
Дата добавления: 2019-09-13; просмотров: 557; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!