Не лежать в одной плоскости и, следовательно, не иметь общих точек.
Определение: Две прямые называются пересекающимися, если они имеют общую точку.
Определение: Две прямые называются параллельными, если они лежат в одной плоскости и не имеют общих точек или совпадают.
 |
Теоремы:
Если две прямые параллельны третьей прямой, то они параллельны.
Если при пересечении двух прямых секущей внутренние накрест лежащие углы равны, то прямые параллельны.
3. Если при пересечении двух прямых секущей сумма внутренних односторонних углов равна 180°, то прямые параллельны.
Замечание: Теоремы о параллельных прямых в пространстве примем без доказательства.
 |
Определение: Две прямые называются скрещивающимися, если они не пересекаются и не параллельны (не лежат в одной плоскости).
Обозначение: a · b
ПРИЗНАК СКРЕЩИВАЮЩИХСЯ ПРЯМЫХ
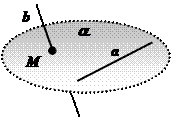
Теорема: Если одна из двух прямых лежит в плоскости, а другая пересекает эту плоскость в точке, не принадлежащей первой прямой, то данные прямые скрещиваются.
Дано: 
; 
; 
.
Доказать: a · b
Вывод:
1. Через скрещивающиеся прямые нельзя провести плоскость.
2. 
Чтобы доказать, что две данные прямые скрещиваются, надо назвать (задать) плоскость, которой одна из этих прямых принадлежит, а другая прямая её пересекает в точке, не принадлежащей первой прямой.
Пример: Известно, что 
. Возможны ли какие-либо случаи взаимного расположения прямых АВ и т, кроме случая, изображенного на рисунке?
|
|
|
Упражнения:
Укажите на модели куба несколько пар его ребер, лежащих на скрещивающихся прямых.
2. Через вершину А ромба АВСD проведена прямая а, параллельная диагонали ВD, а через вершину С – прямая b, не лежащая в плоскости ромба. Докажите, что прямые а и СD пересекаются, прямые а и b скрещиваются.
3. Дано: a · b, 
. Доказать: А1В1 · А2В2 , А1В2 · А2В1.
4. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ
ПРИЗНАК ПАРАЛЛЕЛЬНОСТИ ПРЯМОЙ И ПЛОСКОСТИ
ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ
В пространстве рассматриваются три случая возможного расположения прямой и плоскости, вытекающие из аксиомы:
I3. Прямая, проходящая через две любые точки плоскости, лежит в этой плоскости.
1. Прямая лежит в плоскости (Рис. 1.);
Из аксиомы I3 следует, что если прямая не лежит в плоскости, то она имеет с ней не более одной (одну или ни одной) общей точки.
2. Прямая и плоскость пересекаются (Рис. 2.);
3. 
Прямая и плоскость не имеют общих точек (Рис. 3.).
Определение: Прямая и плоскость называются пересекающимися, если прямая и плоскость имеют одну общую точку (Рис. 2.)
Определение: Прямая и плоскость называются параллельными, если прямая и плоскость не имеют общих точек или когда прямая лежит в плоскости. (Рис. 3, 1.)
|
|
|
Теорема: (вспомогательная) Если плоскости a и b пересекаются и прямая l,принадлежащая плоскости b, параллельна плоскости a, то прямая l параллельна прямой, являющейся пересечением плоскостей a и b .
Дано: 
.
Доказать: 
 | |||
 | |||
Дата добавления: 2019-09-13; просмотров: 899; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!