Значение коэффициента риска и процента Р
| Р % | 5 | 4,5 | 3,6 | 3 | 2,8 | 2,1 | 2 | 1,6 | 1,2 | 1 |
| t | 1,96 | 2,0 | 2,1 | 2,17 | 2,2 | 2,3 | 2,32 | 2,4 | 2,5 | 2,57 |
| Р % | 0,9 | 0,69 | 0,59 | 0,5 | 0,37 | 0,27 | 0,19 | 0,14 | 0,1 | 0,07 |
| t | 2,6 | 2,7 | 2,8 | 2,81 | 2,9 | 3 | 3,1 | 3,2 | 3,3 | 3,4 |
Тогда:
 (15)
(15)
Введя коэффициент относительного рассеяния λ в формулу 15, для закона нормального распределения: λ=  , имеем:
, имеем:
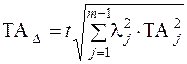 (16)
(16)
Формула 16 устанавливает связь между допуском на замыкающий размер и допуском на составляющие звенья.
lj характеризует закон распределения размеров в зависимости от условий и метода обработки детали, размер которой входит в размерную цепь.
Наиболее часто встречается распределение по нормальному закону, обусловленное действием большого количества случайных факторов. Если размеры распределяются по закону равной вероятности  . При законе равной вероятности –
. При законе равной вероятности –  .
.
Решение задачи с учетом теории вероятности аналогично ее решению на максимум–минимум, только за исходную зависимость принимается формула 16, куда подставляется известная формула: 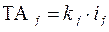
При способе одного квалитета средний квалитет допусков составляющих звеньев получается исходя из условия, что k1=k2=…=km–1=kср. Окончательно имеем:
 (17)
(17)
Пример расчета размерных цепей вероятностным методом.
Пример:
Для возможности сравнения вероятностного метода расчета с расчетом по методу полной взаимозаменяемости рассмотрим ту же размерную цепь (рис. 24).
|
|
|
Необходимо обеспечить осевой зазор АD=0,3+0,2 мм между торцом крышки и наружным кольцом подшипника при нормальном законе распределения рассеяния размеров составляющих звеньев и Р=0,5%.
Закон распределения и процент брака студент назначает сам.
Решение:
1. Определение номинальных размеров составляющих звеньев (этот пункт соответствует 1-му при расчете цепи методом полной взаимозаменяемости).
2. Определение средней точности размерной цепи.
Из табл. 20 при Р=0,5% находим коэффициент t =2,81.
Определим по формуле17 среднее число единиц допуска.

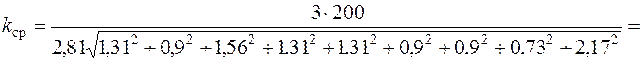 =54,7
=54,7
Найденное число единиц допуска находится ближе к стандартному значению k=64, что соответствует 10-му квалитету.
При расчете размерной цепи вероятностным методом допуски на размеры деталей назначим по 10 квалитету, что снизит стоимость их изготовления по сравнению с меньшими допусками, назначенными по 7 и 8 квалитетам при расчете методом полной взаимозаменяемости.
3. Определение истинного процента брака
Из формулы 16 определим процент брака:

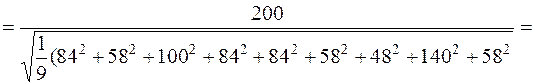
|
|
|
=2,39 ,
что соответствует браку менее 2-х процентов.
Примем, что в данных условиях такой процент брака нас устраивает. Если же потребуется меньший процент брака, то надо будет допуски на ряд звеньев назначить по 9-му квалитету.
4. Определение предельных отклонений звена  .
.
Отклонения составляющих звеньев назначаем по аналогии с методом полной взаимозаменяемости и заносим в табл. 21.
Пользуясь формулой 8, определим координату середины поля допуска звена  :
:


 мкм
мкм
Верхнее отклонение звена  :
:
 мкм
мкм
Нижнее отклонение звена 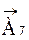 :
:
 мкм
мкм
Таблица 21
Дата добавления: 2019-09-13; просмотров: 322; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
