Моделирование законов распределения

⇐ ПредыдущаяСтр 20 из 27Следующая ⇒

Как было уже ранее отмечено, вероятностная информация может быть неполной, когда неизвестен тип закона распределения или неизвестны его параметры. Чаще всего оказывается неизвестен и тип и параметры закона распределения. Решение в общем виде задачи нахождения закона распределения случайной величины по ее частному распределению, полученному в результате наблюдений, является весьма сложной проблемой. Поэтому на практике поступают иначе – осуществляют моделирование законов распределения (зная, что моделирование осуществляется всегда с некоторой неточностью). Возможны два способа моделирования.

По первому способу выбирают один из известных теоретических законов распределения и определяют степень его сходимости со статистическим.

Второй способ используют тогда, когда статический закон распределения не соответствует ни одному теоретическому закону. В этом случае статистическое распределение сглаживается специальными кривыми (кривыми Пирсона или Романовского), позволяющими его более подробно описать.

Рассмотрим далее первый способ моделирования. Допустим, после обработки статистических данных получен какой-либо вариационный ряд, по данным которого построена некоторая статистическая кривая . Анализ этой кривой показывает, что данные статистического распределения наиболее полно согласуются с некоторой теоретической кривой (например, экспонентой), выраженной функцией распределения . Как бы хорошо ни была подобрана теоретическая кривая, между ней и статистическим распределением неизбежны некоторые расхождения. Естественно, возникает вопрос: объясняются ли эти расхождения только случайными обстоятельствами, связанными с ограниченным числом наблюдений и ошибками измерения, или являются существенными и связаны с тем, что подобранная теоретическая кривая плохо выравнивает данное статистическое распределение. Для ответа на этот вопрос служат так называемые критерии согласия.

Идея применения критериев согласия заключается в следующем. На основе статистического материала проверяется некая гипотеза Н о том, что случайная величина Х подчиняется некоторому определенному закону распределения. Этот закон может быть задан в той или иной форме: в виде функции распределения или в виде совокупности вероятностей , где - вероятность того, что величина Х попадает в пределы -го разряда.

Так как функция распределения является наиболее общей и определяет собой любую другую, то гипотезу Н можно сформулировать следующим образом: величина Х имеет функцию распределения . Чтобы принять или отвергнуть гипотезу Н, рассмотрим некоторую величину , характеризующую расхождение теоретического и статистического распределений. Величина может быть выбрана различными способами: например, в качестве меры расхождения можно взять сумму квадратов отклонений теоретических вероятностей от соответствующих частот или же сумму тех же квадратов с некоторыми коэффициентами («весами»), или максимальное отклонение статистической функции распределения от теоретической и т.д.

Оценка согласованности производится при допущении, что если статистическое распределение подчинено определенному закону распределения , то и вспомогательная случайная величина , выбранная в качестве меры расхождения между теоретическим и статистическим распределениями, определяется тем же законом распределения и тем же числом проведенных опытов .

Предположим, что нам известны закон распределения выбранной меры расхождения для нашего статистического распределения, подсчитанное по результатам испытаний. Тогда, если известна функция распределения меры расхождения , можно определить событие, когда

где 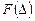- функция распределения меры расхождения;

- конкретное значение меры расхождения для данного статистического распределения;

- вероятность того, что мера расхождения не меньше статистической меры расхождения .

Если эта вероятность мала, гипотезу Н следует отвергнуть, как малоправдоподобную, т.е. теоретическое распределение выбрано неудачно; если же эта вероятность значительна, наше предположение, что статистическое распределение подчинено закону , верно и гипотезу Н следует принять как состоятельную.

Рассмотрим наиболее часто применяемые критерии согласия. Прежде всего - это критерий Пирсона. Пирсон предложил критерий согласия, который дает возможность сравнивать между собой два распределения, причем эти распределения могут быть теоретическими или статистическими, или одно теоретическим, а другое статистическим. Критерий согласия позволяет определить вероятность согласия всей совокупности точек одного распределения с другим. Предположим, что произведено независимых опытов, в каждом из которых случайная величина Х приняла определенные значения, отличающиеся друг от друга на какую угодно величину. Чтобы результаты опытов оформить в виде статистического ряда, весь объем выборки разбивают на равных интервалов. При этом число интервалов, как это уже было ранее отмечено, выбирают исходя из следующих соображений. Во-первых, оно не должно быть слишком большим, так как при этом в каждом интервале окажется малое число наблюдений и закономерность может отчетливо не проявиться, а, во-вторых, число интервалов не должно быть и чрезмерно малым, чтобы не утерять существенных подробностей распределения. Рекомендуется, чтобы в каждом интервале было не менее 15-20 замеров. Если по краям распределения имеются интервалы с числом замеров меньше пяти, то их следует объединить в более крупные, либо не учитывать при обработке данных, если их достоверность недостаточна (т.е. по краям статистическое распределение может быть плохо «обусловлено» из-за ограниченного количества статистических данных).

При решении задач исследования надежности на этот недостаток необходимо обращать особое внимание, т.к. решения обычно принимаются в области, где статистическое распределение плохо «обусловлено». При объеме выборки рекомендуется делить весь диапазон вариации на 6-15 интервалов.

В результате обработки статистических данных имеем интервальный вариационный ряд следующего вида:

Требуется проверить, согласуются ли экспериментальные данные с гипотезой о том, что случайная величина Х имеет закон распределения, заданный функцией .

Зная теоретический закон распределения можно найти теоретические вероятности попадания случайной величины в -й интервал: . В качестве меры расхождения между теоретическим и статистическим распределениями принимаем сумму квадратов отклонений , взятых с некоторыми «весами» (коэффициентами) :

где - статистическая частота попадания случайной величины в -й интервал;

- число значений случайной величины в -м интервале;

- теоретическая вероятность попадания случайной величины Х в -й интервал.

Коэффициенты (веса разрядов) вводят потому, что в общем случае отклонения, относящиеся к различным разрядам нельзя считать равноправными по значимости. Одно и то же по абсолютной величине отклонение может быть малозначительным, если сама вероятность велика, и очень значительным, если она мала. Поэтому «веса» целесообразно взять обратно пропорциональным вероятностям разрядов . Пирсон показал, что если принять 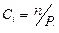, то при достаточно большом значении закон распределения обладает следующими свойствами: он практически не зависит от функции распределения и числа опытов , а зависит только от числа интервалов статистического ряда и параметра , называемого «числом степеней свободы» распределения.

При таком выборе коэффициентов мера расхождения обозначается

Чтобы не иметь дело с малыми дробными числами, можно ввести под знаком суммы, и тогда с учетом, что

Числом степеней свободы называется разность между числом частных интервалов вариационного ряда и числом условных связей , наложенных на случайную величину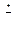

Число связей определяется следующими требованиями:

1). Сумма 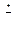равна единице, т.е.:

2). Совпадение математического ожидания с его статистической оценкой

3). Совпадение теоретических и статистических дисперсий

Таким образом, при .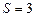

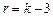Распределение табулировано.

Пользуясь таблицами, можно для каждого значения и числа степеней свободы найти вероятность того, что величина, распределенная по закону , превзойдет это значение.

Схема применения критерия согласия :

1) На основе опытных данных в качестве предполагаемого выбирают вид теоретического закона распределения и находят его параметры.

2) На основе принятого теоретического закона распределения определяют теоретические вероятности попадания случайной величины в -й интервал.

3) Вычисляют величину и числа степеней свободы .

4) По полученным значениям и с помощью таблиц определяют - вероятность того, что величина, имеющая распределение с степенями свободы, превзойдет данное значение .

5) Если вероятность настолько мала, что событие с такой вероятностью можно считать практически невозможным, гипотезу о предполагаемом законе распределения рассматриваемой случайной величины следует отвергнуть как несостоятельную; если вероятность сравнительно велика, то расхождения между теоретическим и статистическим распределениями считают несущественными и гипотезу о выбранном законе распределения рассматриваемой случайной величины принимают как правдоподобную.

Насколько же должна быть мала вероятность , чтобы отвергнуть (или пересмотреть) гипотезу о принятом законе распределения. Нет математического решения этого вопроса. На практике принято: если меньше 0.1 , то гипотезу отвергают.

Кроме критерия согласия Пирсона для оценки сходимости теоретического и статистического распределений на практике используют еще ряд критериев, и в том числе критерий согласия А.Н. Колмогорова.

В качестве меры расхождения между статистическим и теоретическим распределения по критерию А.Н. Колмогорова принимается максимальное абсолютное значение модуля разности между статистической функцией распределения и соответствующей ей теоретической функцией распределения :

Затем подсчитывается

А.Н. Колмогоров показал, что независимо от функции распределения непрерывной случайной величины Х при неограниченном возрастании числа наблюдений вероятность неравенства стремится к пределу, определяющему уравнением

Если 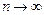, то можно считать, что . Значения табулированы.

Схема применения критерия согласия А.Н. Колмогорова следующая:

1) Строят теоретическую и статистическую функции распределения.

2) Определяют максимальную величину модуля разности .

3) Подсчитывают .

4) По величине из таблиц определяют .

5) Формируют вывод, руководствуясь общими принципами применения критериев согласия: если функция оказывается больше 0,25, функцию принимают за истинную гипотезу; если оказывается меньше 0,05, функцию считают не отвечающей действительности.

Дата добавления: 2019-09-13; просмотров: 401; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 15 16 17 18 192021 22 23 24 Следующая ⇒

Мы поможем в написании ваших работ!