Закон распределения Вейбулла-Гнеденко
Распределение Вейбулла-Гнеденко используют при определении уровня надежности элементов в период приработки и установления наработки на отказ неремонтируемых изделий. Это распределение двухпараметрическое. Его параметрами являются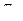 
и 
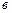- положительные постоянные. Дифференциальная функция (плотность вероятности) распределения имеет вид
.
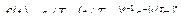Интегральная функция распределения Вейбулла-Гнеденко
.
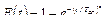Вероятность безотказной работы
.
При 
распределение Вейбулла-Гнеденко превращается в экспоненциальное, а при 
- в распределение Релея.
Основные характеристики для распределения Вейбула-Гнеденко приведены на рис. 5.3.
а)
б)
Рис. 5.3. График дифференциальной (а) и интегральной (б)
функции распределения Вейбулла-Гнеденко при различных значениях в.
Закон распределения Пуассона
Распределение Пуассона применяется для исследования дискретных случайных величин при условии, что события происходят независимо друг от друга с постоянно средней интенсивностью за одинаковые промежутки времени. К таким величинам относится число отказов элемента за определенный промежуток времени.
Случайная величина распределена по закону Пуассона, если вероятность того, что она примет значение 
выражается формулой
|
|
|
,
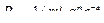где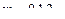 
- возможные значения случайной величины;
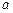- положительная величина, характеризующая интенсивность появления событий в 
испытаниях (параметр распределения).
Если в среднем в единицу времени наступает 
отказов и 
, то тогда
.
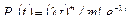Если поток отказов простейший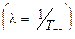 
, то тогда
,
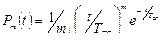где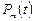 
- вероятность появления в период 
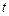равно отказов;
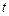- время, для которого определяется вероятность появления отказов;
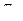- среднее время безотказной работы системы.
Таким образом, можно вычислить вероятность появления в системе любого числа отказов от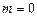 
до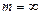 
при заданном относительном времени 
.
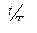Статистическая оценка законов распределения
Для исследования надежности ЭЭС необходимо знать законы распределения наблюдаемых случайных величин: наработки на отказ, времени восстановления, числа отказов и т.д. При эксплуатации ЭЭС в течение некоторого времени 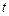рассматриваемая случайная величина может принять различных определенных значений. Совокупность этих случайных значений случайной величины в математической статистике получила название статической выборки объемом . Если расположить отдельные значения случайной величины в возрастающем порядке и указать относительно каждого значения, как часто оно встречается в данной совокупности, то получим распределение случайной величины, или вариационный ряд, на основании которого можно определить аналитическую форму неизвестной плотности вероятностей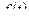 
или функцию распределения 
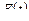и оценить входящие в эту функцию параметры.
|
|
|
Построение вариационного ряда осуществляется следующим образом. Весь диапазон значений рассматриваемой случайной величины разбивают на интервалы. Затем подсчитывают количество значений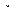 
случайной величины, приходящееся на каждый интервал, и определяют частоту ее попадания в данный интервал по формуле
,
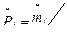где 
- частота попадания случайной величины в i-й интервал;
- объем выборки.
Определив таким образом частоту попадания случайной величины 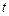в каждый интервал, получают интервальный вариационный ряд, который изображается в виде таблицы, в которой указаны интервалы и соответствующие им частоты:
Интервал 
… 
… 
.
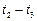Частота 
.
|
|
|
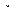
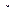
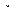Для выбора оптимальной величины интервала, при которой вариационный ряд не будет очень громоздким и в нем не исчезнут особенности изучаемого явления, можно пользоваться формулой [5]
,
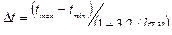где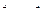 
- размах вариации случайной величины ;
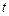- объем выборки.
Число интервалов в соответствии с данной формулой может быть определено как
.
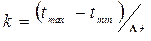Для приближенного расчета величины интервалов можно пользоваться формулой
,
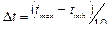но при этом в каждом i-ом интервале количество значений 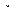должно быть не меньше 15-20.
Для наглядного изображения вариационного ряда прибегают к его графическому изображению, чаще всего к гистограмме и статистической функции распределения.
Статистическая функция распределения строится следующим образом. Над каждым отрезком оси абсцисс (рис. 5.4), соответствующим расстоянию между концами интервалов, проводится горизонтальная прямая на уровне ординаты, равной величине частоты, а затем концы горизонтальных отрезков соединяются вертикальными линиями.
Статистическая функция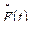 
представляет собой частоту событий 
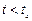в данной выборке
,
|
|
|
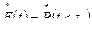где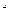 
- текущая переменная;
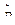- частота, или статистическая вероятность события.
Значение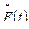 
при данном значении 
определяется по формуле
,
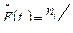где 
- число событий, при которых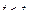 
.
При неограниченном увеличении числа наблюдений частота событий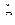 
, согласно теореме Я. Бернулли, приближается к вероятности этого события. Если 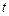наработка на отказ, то график функции 
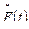приближается (рис. 5.5) к плавной кривой 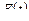- интегральной функции распределения величин 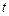, т.е. к вероятности отказа 
.
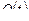Рис. 5.4. Статистическая функция распределения случайной величины .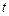
Рис. 5.5. Функция распределения случайной величины .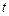
Дата добавления: 2019-09-13; просмотров: 882; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!