Расчет зубьев цилиндрической косозубой и шевронной передач на изгиб

3.57. Расчет на изгиб косых и шевронных зубьев аналогичен расчету прямых зубьев.

Так как в косозубой и шевронной передачах зубья значительно прочнее прямых зубьев, то соответственно в расчетные формулы (3.5), (3.9) вводят коэффициенты, учитывающие повышение прочности при изгибе по срав­нению с прямыми зубьями.

Коэффициент формы зуба Y_F выбирают по табл. 3.6 в зависимости ет эквивалентного числа зубьев приведенного колеса (см. рис. 3.44):

z _э = z_v = z/cos³β,

где z_v — число зубьев приведенного (эквивалентного) колеса в сечении Б—Б (рис. 3.44); z — фактическое число зубьев; β — угол наклона зубьев.

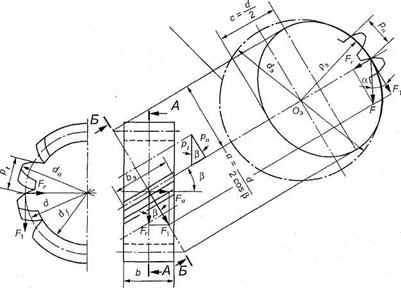
Рис. 3.44. К расчету косозубых колес.

Определение параметров приведенного цилиндрического колеса

Как влияет угол наклона зубьев на величину осевой силы (см. рис. 3.44)?

Если зубчатое колесо рассечь нормальной плоскостью (см. рис. 3.44), то в сечении начального цилиндра получим эллипс с полуосями а = d/2cosβ и с = d /2. Профиль зуба в этом сечении близок к профилю та­кого прямого зуба модуля т_п, который расположится на цилиндрическом колесе радиусом ρ_э = d _э /2, равным радиусу кривизны эллипса. Это колесо называется эквивалентным (приведенным) колесом. Радиус кривизны эл­липса. р_э = а²/с = d/(2cos²β). Диаметр эквивалентного колеса d ₃ = 2 p ₃ = = d / cos ² β . Если в последнее выражение подставить d = ( m_nz )/ cosβ , то полу­чится число зубьев эквивалентного колеса (эквивалентное или фиктивное число зубьев):

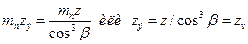
При одних и тех же силовых параметрах передачи косозубая передача по сравнению с прямозубой имеет меньшие или большие габариты?

3.58. Проверочный расчет.

По аналогии с формулой (3.5) условие прочности зубьев на изгиб ци­линдрической косозубой передачи отличается введением поправочных ко­эффициентов:

учитывающего перекрытие зубьев Y_ε = 1/К_εε_а;

учитывающего угол наклона зуба Y_β ≈ cos β (при β = 8 ÷ 18° среднее зна­чение Y_β = 0,9);

учитывающего распределение нагрузки между зубьями К _{F а} (выбирается по табл. 3.14).

 

 

Таблица 3.14. Значение коэффициента KHα , KFα
Степень точно­сти передачи	Кца при окружной скорости v , м/с			К Fa
	5	10	15
6	1,01	1,03	1,04	0,72
7	1,05	1,07	1,09	0,81
8	1,09	1,13	—	0,91

Приняв Y_εY_β = 0,9, формула проверочного расчета косозубых передач нг изгиб имеет вид

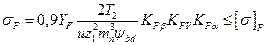                                   (3.23)

где Т₂ — вращающий момент на колесе, Н • мм; и — передаточное числе; Ψ_bd=0,2 ÷ 1,4 — коэффициент длины зуба (табл. 3.7); Y_F — коэффициент формы зуба (табл. 3.6 выбирается по эквивалентному числу зубьев шестер­ни z_v ); z — число зубьев; m_n  — нормальный модуль, мм; K_{F β} K_Fv — коэффи­циенты расчетной нагрузки (см. табл. 3.4 и 3.5); [ σ ] _F — допускаемое напря­жение при изгибе, МПа (выбирается, см. шаг 3.39).

Расчет косозубых передач на изгиб ведется по менее прочному зубу. которого отношение [о] _F / Y_F меньшее.

3.59. Проектировочный расчет.

С учетом формулы (3.8) из формулы  (3.23)

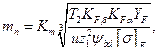                                           (3.24)

где т _n — нормальный модуль, мм; Т₂ — вращающий момент, Н · мм; [σ] _F — допускаемое напряжение при изгибе, МПа; К_т — вспомогательный коэф­фициент (см. шаг 3.38) (для косозубых передач К_т учитывает также Y_ε и Y_β .

Для условия z = 24, β = 36°52'12" выберите из табл. 3.6 коэффициент формы зуба Y_F .

 

---

Дата добавления: 2019-09-13; просмотров: 335; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!