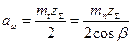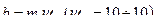Цилиндрические косозубые и шевронные зубчатые передачи . Устройство и основные геометрические и силовые соотношения

⇐ ПредыдущаяСтр 24 из 84Следующая ⇒

3.49. Косозубые зубчатые передачи, как и прямозубые, предназначены для передачи вращательного момента между параллельными валамя (рис. 3.36). У косозубых колес оси зубьев располагаются не по образующей делительного цилиндра, а по винтовой линии, составляющей с образующей угол β (рис. 3.44). Угол наклона зубьев р принимают равным 8÷18°, он одинаков для обоих колес, но на одном из сопряженных колес зубья наклонены вправо, а на другом влево.

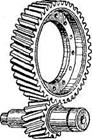
Рис. 3.36. Цилиндрическая косозубая передача

Передаточное число для одной пары колес может быть и ≤ 12. В прямозубых передачах линия контакта параллельна оси, а в косозубых расположена по диагонали на поверхности зуба (контакт в прямозубых передачах осуществляется вдоль всей длины зуба, а в косозубых — сначала в точке увеличивается до прямой, «диагонально» захватывающей зуб, и постепенно уменьшается до точки).

Достоинства косозубых передач по сравнению с прямозубыми: уменьшение шума при работе; меньшие габаритные размеры; высокая плавность зацепления; большая нагрузочная способность; значительно меньшие дополнительные динамические нагрузки.

За счет наклона зуба в зацеплении косо-зубой передачи появляется осевая сила.

Направление осевой силы зависит от направления вращения колеса (рис. 3.37), направления винтовой линии зуба, а также от того, каким является колесо — ведущим или ведомым. Осевая сила дополнительно нагружает валы и опоры, что является недостатком косозубых передач.

Рис. 3.37. Усилия в косозубой цилиндрической передаче

3.50. Шевронные зубчатые колеса пред ставляют собой разновидность косозубых колес (рис. 3.38).

а) б)

Рис. 3.38. Шевронная зубчатая передача

Цилиндрическое зубчатое колесо, венец которого по ширине состоит из участков с правыми и левыми зубьями (рис. 3.38, а), называют шевронным колесом. Часть венца зубчатого колеса, в пределах которого линии зубьев имеют одно направление, называют полушевроном. Различают шевронные колеса с жестким углом (рис. 3.38, б), предназначенным для выхода режущего инструмента при нарезании зубьев. Шевронные передачи обладают всеми преимуществами косозубых, а осевые силы (рис. 3.39) противоположно направлены и на подшипник не передаются.

Рис. 3.39. Усилия в зацеплении шевронных зубчатых колес

В этих передачах допускают большой угол наклона зубьев (β = 25 ÷ 40°). Ввиду сложности изготовления шевронные передачи применяют реже, чем косозубые, т. е. в тех случаях, когда требуется передавать большую мощность и высо-кую скорость, а осевые нагрузки нежелательны.

Рис. 3.40

Будет ли возникать осевая сила в передаче, состоящей из зубчатых колес (рис. 3.40)? Чем отличается эта передача от косозубой?

3.51. Косозубые и шевронные колеса в отличие от прямозубых имеют два шага и два модуля: в нормальном сечении (см. рис. 3.44) по делительной окружности — нормальный шаг р_п, в торцовой плоскости — торцовый шаг р _t . Из условия, что модуль зацепления равен шагу, деленному на число π, имеем т_п = р₁/π; т _t = р _t /п.

Для косозубых и шевронных колес значения нормального модуля т _n стандартизованы, так как профиль косого зуба в нормальном сечении соответствует исходному контуру инструментальной рейки и, следовательно, т = т_п (косозубые и шевронные колеса нарезают, тем же способом и инструментом, что и прямозубые). Нормальный модуль т_п является исходным при геометрических расчетах.

Определим зависимость между нормальным и торцовым шагом и модулех через угол наклона зубьев.

Если левую и правую части разделим на л, получим

m_n = m_t cosβ; m_t = m_n /cosβ.

3.52. Геометрические параметры цилиндрической косозубой и шевронной передач с эвольвентным профилем зуба рассчитают по формулам, приведенным в табл. 3.13. По торцовому модулю т _t рассчитывают делительные (начальные) диаметры, а до т_п — все остальные размеры зубчатых колес.

Таблица 3.13. Геометрические параметры цилиндрической косозубой передачи

Параметр, обозначение	Расчетные формулы
Нормальный модуль т„
Торцовый (окружной модуль) т _t
Диаметр вершин зубьев d_a
Делительный диаметр d
Диаметр впадин зубьев d_f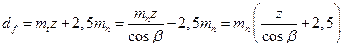
Шаг нормальный р _n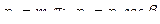
Шаг торцовый (окружной) р _t
Окружная толщина зубьев S_t
Ширина впадин зубьев e_t

Параметр, обозначение	Расчетные формулы
Высота зуба h	h = 2,25m_n
Высота головки зуба h_a	h_a = m_n
Высота ножки зуба h_f	h_f.=l,25m_n
Радиальный зазор с	с = 0,25m_n
Межосевое расстояние a_ω
Длина зуба b
Ширина венца b_ω

Окружная сила F_t = P / v . На косой зуб действует осевая сила F_a = F_t tgα (см. рис. 3.37), радиальная (распорная) сила F_r = F_t tga/cosβ.

Определите т_п и m_t, если известны делительный диаметр и межосевое расстояние.

3.53. В косозубдй передаче сила F , действующая на зуб косозубого колеса
(см. рис. 3.44), направлена по нормали к профилю зуба, т. е. по линии зацепле
ния эквивалентного прямозубого колеса, и составляет угол а с касательной к
эллипсу.

Эту силу разложим на две составляющие: окружную силу на эквивалентном колесе F_t и радиальную (распорную) силу на этом колесе F_r .

Если, в свою очередь, силу F _} разложить по двум направлениям, то получим такие силы: F , — окружную силу, F_a — осевую.

3.54. Для зубчатого колеса с шевронным зубом окружную силу F ₁ и рас
порную F_r определяют по тем же формулам, что и для косозубой передачи,
т. е. F_t = P / v , F_r = F_t tgα/cosβ. В шевронной передаче осевая сила F_a = 0 (см.
рис. 3.39).

Почему в шевронной передаче (см. рис. 3.38) осевая сила равна нулю?

3.55. Винтовая передача (разновидность косозубой) состоит из двух косозубых цилиндрических колес (рис. 3.42). Однако в отличие от косозубых цилиндрических передач с параллельными валами касания между зубьями здесь происходит в точке и при значительных скоростях скольжения. Поэтому при значительных нагрузках винтовые зубчатые передачи работать удовлетворительно не могут.

По рис. 3.42 определите, как расположены оси валов у винтовой передачи.

Рис. 3.41. Винтовая зубчатая передача

3.56. Ответить на вопросы контрольной карточки 3.8.

Контрольная карточка 3.8
Вопрос	Ответы	Код
Покажите на рис. 3.42 нормальный шаг зубьев р„	Х₁ Х₂ Х₃ Х₄ На рисунке не показан	1 2 3 4 5
В каких пределах принимают угол наклона зубьев (р) для косозубой зубчатой передачи?	8 ÷ 18° 25 ÷ 45° 20° 90°	6 7 8 9
Какой модуль принимают стандартным при расчете косозубой зубчатой передачи?	Т _n т _t Оба	10 11 12
Укажите формулу для расчета передаточного числа косозубой передачи, если известны диаметры, показанные на рис. 3.43	da/da da₂/da_x d/d₂ d₂/d\	13 14 15 16
По какому модулю рассчитывают делительный размер в косозубой передаче?	Т _n m_y По обоим

Рис. 3.42

Рис. 3.43

Дата добавления: 2019-09-13; просмотров: 682; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 19 20 21 22 232425 26 27 28 Следующая ⇒

Мы поможем в написании ваших работ!