Взаимное расположение прямых на плоскости.

 

Каноническое уравнение	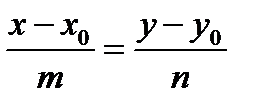Общее уравнение Ax + By + C = 0	Уравнение с угловым коэффициентом y = kx + b
Параллельность
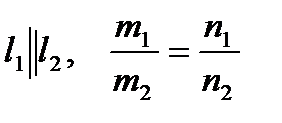
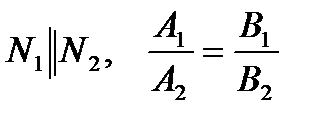
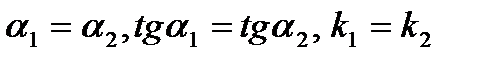
Перпендикулярность
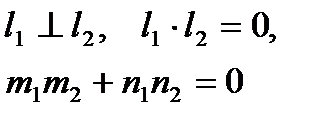
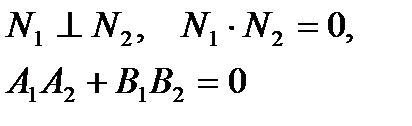
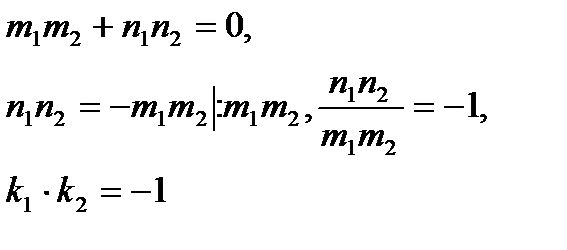
Угол между прямыми

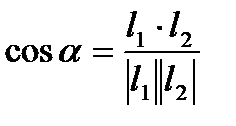
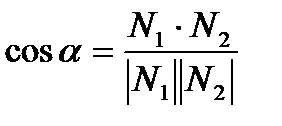
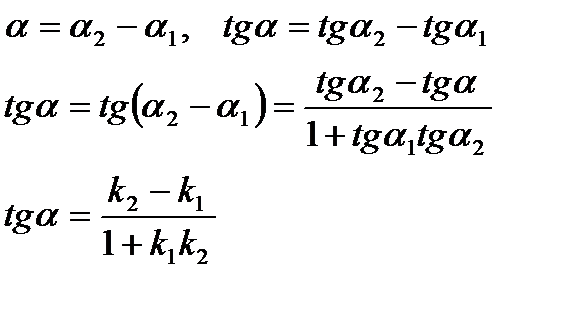
Кривые второго порядка.

Общее уравнение 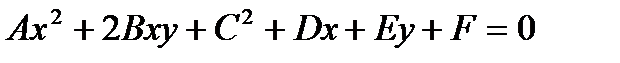. Будем рассматривать окружность, эллипс, гиперболу, параболу.

 

Окружность.

Определение: Окружностью называют множество точек плоскости, удаленных от заданной точки (центра окружности) на заданное расстояние (радиус окружности).

Пусть центр окружности С (а, b ) и радиус равен R, т. М (х, у)- текущая точка.

b

0

а

у

х

По определению │СМ│= R.

,

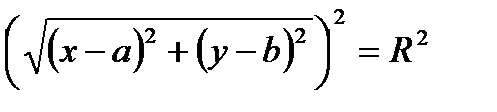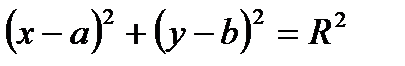 - нормальное уравнение окружности.

 

Если центр окружности находится в начале координат, т.е. С(0;0). Отсюда следует, что 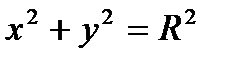- каноническое уравнение окружности.

 

Замечание:

1) Если в общем уравнении кривой второго порядка отсутствуют произведения x, y и коэффициенты при x² и y² равны, то это обязательно уравнение окружности, которое можно получить, выделяя полные квадраты по каждой переменной.

2) Может оказаться, что после выделения полных квадратов уравнение окружности примет вид 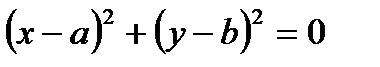,  центр окружности С(а,b), а радиус R= 0. Это уравнение вырожденной окружности. Может оказаться, что  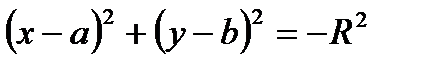- мнимая окружность (без рисунка).

3) Через любые три точки, не лежащие на одной прямой можно провести единственную окружность.

 

Эллипс.

Определение: Эллипсом называется множество точек плоскости, сумма расстояний от каждой из которых до двух заданных точек (фокусов), есть величина постоянная, равная 2а, большая, чем расстояние между фокусами.

Расположим эллипс так, чтобы фокусы находились на оси ОХ на одинаковом расстоянии от начала координат. Обозначим расстояние между фокусами │F₁F₂│=2c.

y

c

0

-c

F2

F1

M(x, y)

x

F₁ (-c, 0) - левый фокус,  F₂ (с, 0) - правый фокус.

т. М (х, у)- текущая точка эллипса.

По определению: │F₁ M│+│F₂M│=2a.

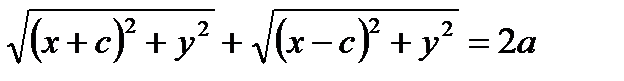
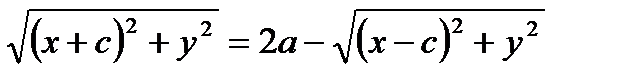
Возведем обе части в квадрат:

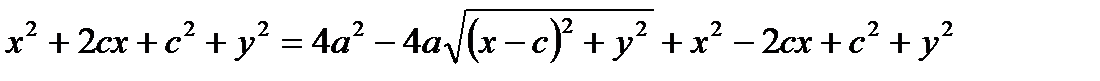
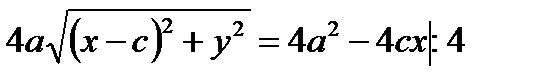
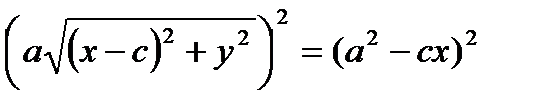
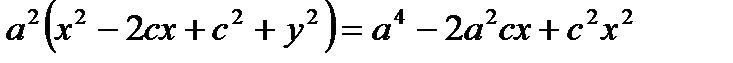
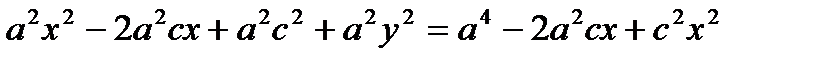
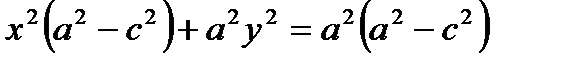
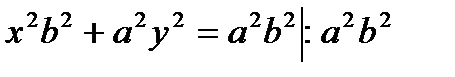
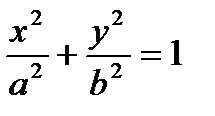 - каноническое уравнение эллипса.

Для построения проанализируем это уравнение:

1) Т.к. уравнение четно по х и у, то эллипс симметричен относительно осей ОХ и ОУ, поэтому достаточно будет построить эллипс в первой четверти и сделать симметрию относительно осей координат.

Выразим из канонического уравнения у через х:

-

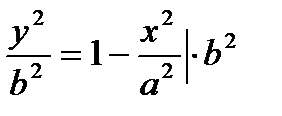
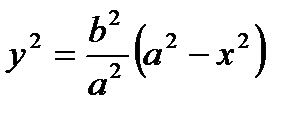
а

-а

-

+

                                   

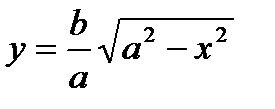
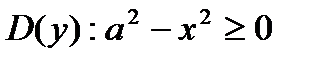
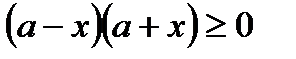
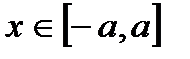
2) Найдем у(0)= b, y(a)= 0. С ростом х, уменьшается у.

Отрезок [0, а] на ОХ - большая полуось, [0, b] - малая полуось эллипса.

т. (а, 0) - правая вершина, т. (-а, 0) - левая вершина, т. (0, b) - верхняя вершина, т. (0, -b) - нижняя вершина, с - фокусное расстояние.

Так как a²-c²= b², то c²= a²-b²- соотношение, связывающее три параметра эллипса.

Определение: Мерой сжатия эллипса является эксцентриситет: .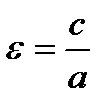

Для эллипса: 0< 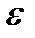<1.

Если эксцентриситет стремится к 0, то эллипс будет стремиться к окружности. Если эксцентриситет стремится к 1, то эллипс будет стремиться к отрезку.

Гипербола.

Определение: Гиперболой называют множество точек плоскости, разность расстояний от каждой из которых до двух заданных точек (фокусов) есть величина постоянная, равная 2а, меньшая, чем расстояние между фокусами, но больше 0.

Расположим гиперболу так, чтобы фокусы находились на оси ОХ на одинаковом расстоянии от начала координат.

│F₁F₂│=2c.

y

c

0

-c

F2

F1

M(x, y)

x

F₁ (-c, 0) - левый фокус,  F₂ (с, 0) - правый фокус.

т. М (х, у)- текущая точка гиперболы.

По определению: │F₁ M│-│F₂M│=2a.

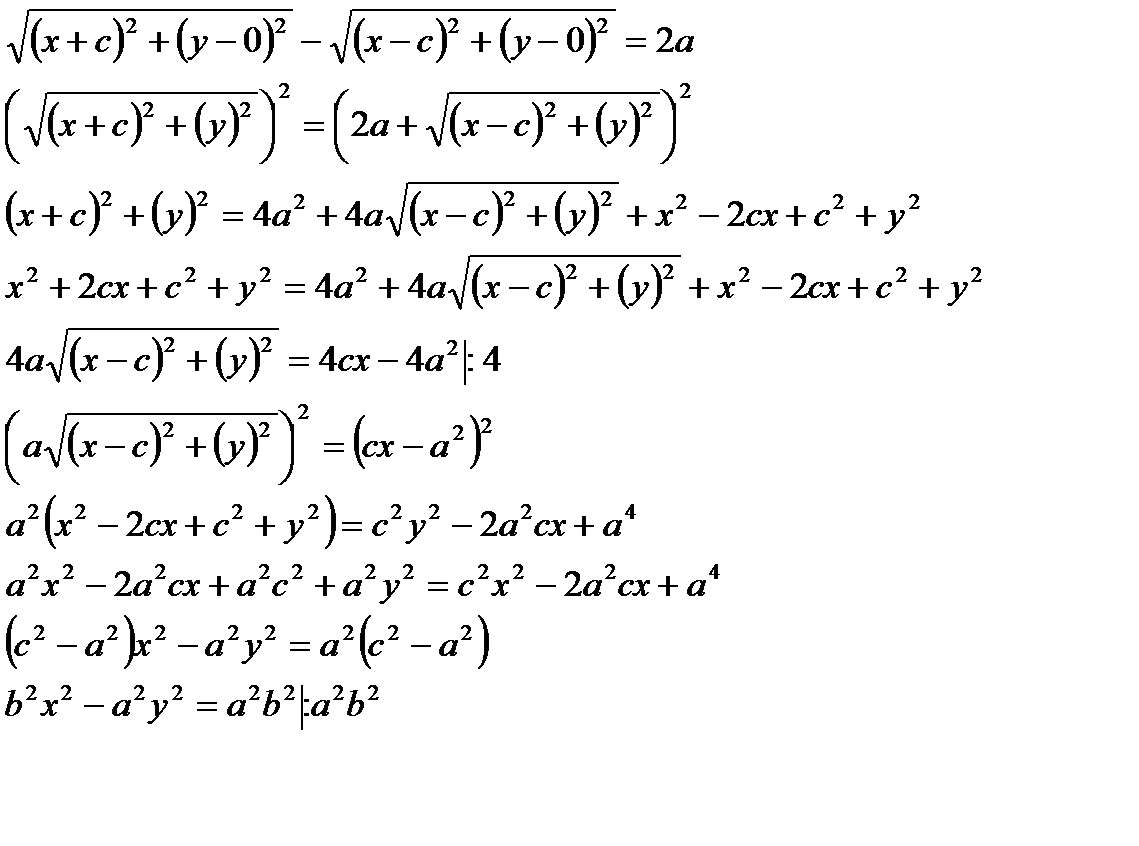
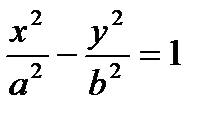 - каноническое уравнение гиперболы.

Исследуем это уравнение:

1) Так как уравнение чётно по х и по у, то гипербола симметрична относительно осей  ОХ и ОУ. Следовательно, построим ее в первой четверти и сделаем симметрию относительно осей координат.

Выразим из уравнения у:

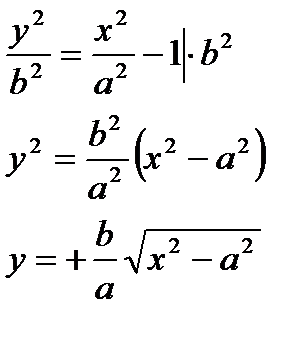
Так как x²- a² ≥ 0, тогда (х-а) (х+а) ≥ 0.

+

+

-

-а

а

х

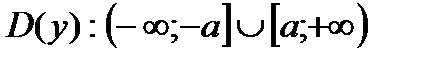
2) При x= a: y= 0. При возрастании х, увеличивается у. При х 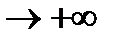 гипербола стремится к прямой .

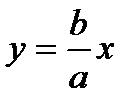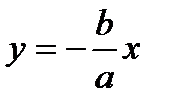
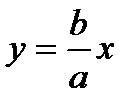
c

F2

F1

a

A

-a

B

b

b

x

y

-c

т. А (а, 0) - правая вершина гиперболы, т. В (-а, 0) - левая вершина.

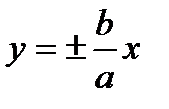- асимптота.

  - осевой прямоугольник.

[0, а] - на ОХ действительная полуось гиперболы.

[0, b] - на ОУ мнимая полуось.

с - фокусное расстояние.

с²= а²+ b² - соотношение для гиперболы.

Мера сжатия эксцентриситет 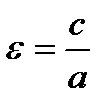. Так как а < с, отсюда следует, что ε> 1.

Парабола.

Определение: Параболой называют множество точек плоскости, расстояние от каждой из которых до заданной точки (фокуса) равно расстоянию до заданной прямой (директрисы).

Расположим параболу так, чтобы начало координат находилось посредине между F и директрисой, причем фокус лежал на оси ОХ.

Обозначим расстояние между F и директрисой - p.

Фокус: F( ).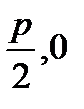

уравнение директрисы: х= .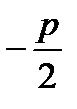

т. М (х, у) - текущая точка параболы.

 

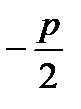
y

N( )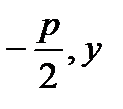

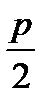
F

M(x, y)

х

По определению параболы: │FM│=│NM│.

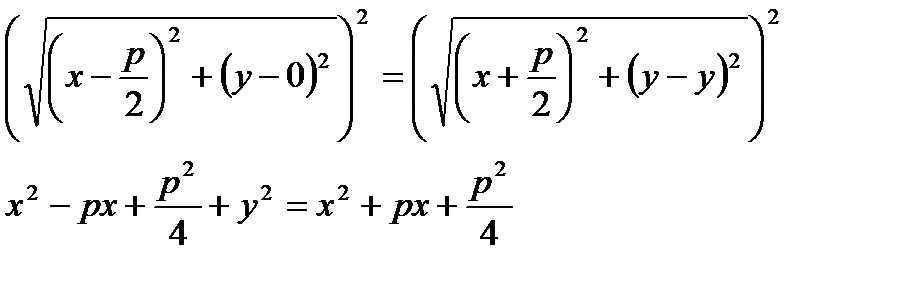
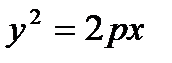 - каноническое уравнение параболы.

Анализ:

Так как уравнение четно по у, то парабола симметрична относительно оси ОХ.

При х= 0: у= 0. С возрастанием х, увеличивается у.

P - параметр параболы.

т. О(0,0) - вершина.

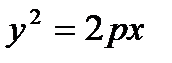: ось симметрии - ось ОХ, p > 0 -график ; p < 0- график .

Аналогично можно вывести каноническое уравнение параболы с осью симметрии ОУ.

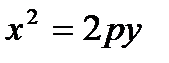: ось симметрии – ось ОУ, p > 0 –график   ; p < 0- график   .

Сфера в пространстве.

Определение: Сферой называют множество точек пространства, равноудаленных от заданной точки (центр сферы) на заданное расстояние (радиус сферы).

Пусть центр сферы С(a, b, c), радиус R, т. М (х, у, z) - текущая точка сферы.

По определению: │СМ│= R.

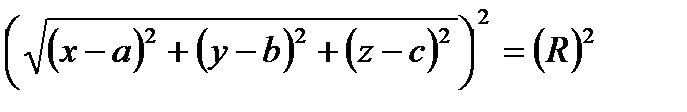
M(x, y, z)

y

z

х

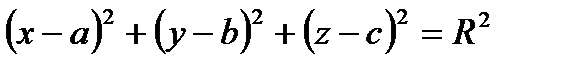- нормальное уравнение сферы.

Если центра сферы - О(0, 0, 0), тогда

x²+ y²+ z²= R² - каноническое уравнение сферы.

Замечание:

В пространстве различают поверхности двух видов:

1) поверхности первого порядка Ax+ By+ Cz+ D= 0 (уравнение плоскости)

2) поверхности второго порядка

Ax²+ By²+ Cz²+ 2Dxy+ 2Fyz+ Kx+ My+ Nz+ L= 0.

Примером поверхности второго порядка служит сфера, остальные поверхности второго порядка: цилиндры, конусы, параболы и другие.

 

 

Скалярное произведение	Векторное произведение	Смешанное произведение
Определение
число   а• b =│а│·│ b │ cos φ	a ´ b= вектор с, что 1° │с│=│ a │·│ b │ sin φ, где Ðj= a,b 2° вектор c ^ a , c ^ b, т.е. с ^ плоскости, в которой лежат вектора а и b. 3° кратчайший поворот от вектора a к b , видимый с конца вектора с будет против часовой стрелки.	число   а bc = ( a ´ b ) • с
Свойства
1° a • b = b • a 2° a • b= 0, т.к. a ┴ b 3° (λa)• b= λ(a• b) 4° a•(b + c)= a• b + a• c 5° а • а = │a│2	1° антикоммунитативность a ´ b = - b ´ a 2° (λ a ) ´ b = λ ( a ´ b ) 3° a ´ ( b + с)= a ´ b + a ´ с 4° a ´ а= 0	1° abc= - bac= bca= ... 2° ( λ a)bc= λ(abc) 3° (a+ b) cd= acd+ bcd 4° ijk= (i×j)· k= k· k= │k│2= 1 ijk= 1
Вычисление в координатной форме
a•b= ax bx + ay by + az bz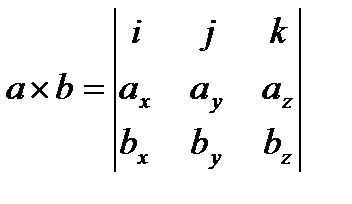
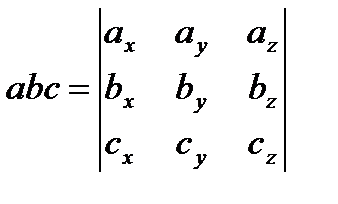
Приложения
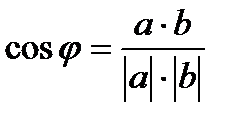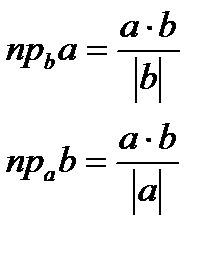
1) 2)Ðj - острый, cosj>0, отсюда следует: a•b> 0. Ðj - тупой, cosj<0, отсюда следует: a•b< 0. Ðj=90°, cosj=0, отсюда следует: a•b= 0. 3)	1) S пар =│ a ´ b │ 2) 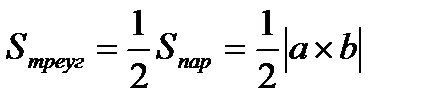3) a║b, отсюда следует, что │ a´b│= 0.	1) V парал = │ abc │ 2) V тетр = 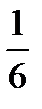V парал V тетр = 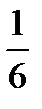│ abc │ 3) если abc >0, то тройка векторов правая; если abc <0, то тройка векторов левая. 4) abc – компланарные: abc =0.

 

---

Дата добавления: 2019-09-13; просмотров: 203; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!