Связь между координатами вектора и проекциями вектора на координатной оси.

проекция

y2

y1

· A(x1, y1, z1)

y

x

z

О

В (x2, y2, z2)

пр _OY АВ= y₁- y₂, пр _OX АВ= x₁- x₂, пр _OZ АВ= z₁- z₂.

Вывод: проекции вектора на координатные оси совпадают с координатами вектора.

 

Условие коллинеарности двух векторов.

а

b

Возьмем два коллинеарных вектора а= (а_х, а_у, а _z ) ║b = ( b_x , b_y , b_z ).

b = λ a.

В координатной форме:

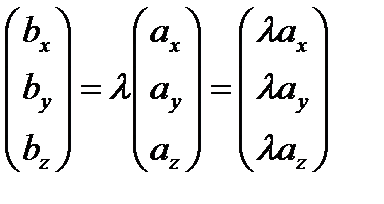
Сравнивая соответствующие координаты первые, вторые и третьи получим:

                                                        .

                           

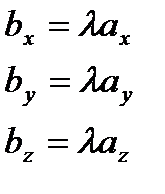
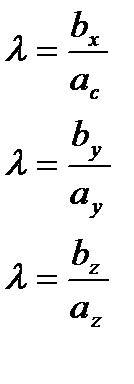
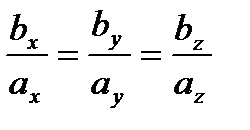Условие коллинеарности: Для коллинеарности двух векторов необходимо и достаточно, чтобы их соответствующие координаты были пропорциональны.

Замечание: если одна из координат вектора равна 0, то у коллинеарного вектора соответствующая координата тоже равна 0.

 

Скалярное произведение векторов.

Определение: Скалярным произведением двух векторов называется число равное произведению длин этих векторов (модулей) на косинус угла между векторами.

По определению: a • b = │ a │·│ b │· cos φ.

, .

, .

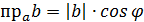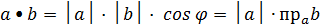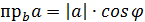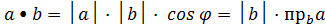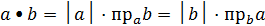 - связь между скалярным произведением и проекцией вектора на вектор.

Свойства скалярного произведения.

1° коммутативность: a • b = b •· a.

a • b= │a│·│b│· cos φ= │b│·│a│· cos φ= b • a.

 

2° условие перпендикулярности: a • b = 0, т.к. a _┴ b или a или b= 0.

1. a _┴ b, φ = 90°, cos 90°= 0, a • b= │a│·│b│·0= 0.

2. a= 0, │a│= 0, a • b= 0 ·│b│· cos φ= 0 .

 

3° (λa)•b= λ(a•b).

(λa)•b= │λa│·│b│· cos φ=λ│a│·│b│· cos φ= λ(a•b).

 

4° a•(b + c)= a•b + a•c.

a•(b + c)= │a│· 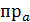(b + c)= │a│·( пр_а b + пр_а c)= │a│· пр_а b +│a│· пр_а c=

= a • b + a • c.

 

5° скалярный квадрат: а • а= │ a │².

а • а=│ a │·│а│· cos 0°=│ a │².

Следствие: .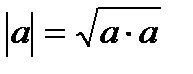

Скалярное произведение координатных ортов.

i × j= 0, так как i ^ j (из 2°);

i × k= 0, так как i ^ k (из 2°);

k × j= 0, так как k ^ j (из 2°);

i × i=│i│² = 1²=1;

j × j=│j│² = 1²=1;

k × k=│k│² = 1²=1.

 

Скалярное произведение в координатной форме.

Возьмем два вектора в координатной форме

а= (а_х, а_у, а _z )= a_xi + a_yj + a_zk , b = ( b_x , b_y , b_z )= b_xi + b_yj + b_zk.

a • b = ( a_xi + a_yj + a_zk )•( b_xi + b_yj + b_zk )= a_xi • b_xi + a_xi • b_yj + a_xi • b_zk + a_yj • b_xi +

+ a_yj• b_yj + a_yj •b_zk + a_zk •b_xi + a_zk•b_yj + a_zk •b_zk = a_x b_x i• i + a_x b_y i•j + a_x b_z i•k+

+a_y b_x i• j + a_y b_y j• j + a_y b_z i• k + a_z b_x i•k + a_z b_y k• j + a_z b_z k•k=

= a_x b_x + a_y b_y + a_z b_z.

Если векторы заданы в координатной форме, то для вычисления скалярного произведения используем формулу:

a • b= a_x b_x + a_y b_y + a_z b_z.

 

Приложения скалярного произведения.

1) Угол между векторами:

.

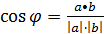Ðj - острый, cos j> 0, отсюда следует, что a • b > 0.

Ðj - тупой, cos j< 0, отсюда следует, что a • b < 0.

Ðj= 90°, cos j= 0, отсюда следует, что a • b = 0.

 

2) Проекция вектора на вектор:

.

 

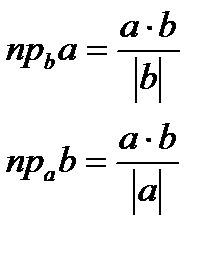Векторное произведение двух векторов.

Определение: Векторным произведением a ´ b векторов a и b называется третий вектор с, обладающий следующими свойствами:

1° │с│=│ a │·│ b │· sin φ, где Ðj= a,b;

2° вектор c ^ a , c ^ b, т.е. с ^ плоскости, в которой лежат вектора а и b;

3° кратчайший поворот от вектора a к b , видимый с конца вектора с будет против часовой.

Свойства векторного произведения:

1° антикоммутативность: a ´ b = - b ´ a .

a ´ b= с , b ´ a= - с .

2° ( λ a) ´ b= λ (a ´ b).

3° a ´ (b + с )= a ´ b + a ´ с.

4° a ´ а = 0.

│ a ´ а │=│ a │·│а│ sin 0°= 0. Отсюда следует, что a ´ а= 0.

 

Векторные произведения координатных ортов.

i

k

j

Если первый орт умножить векторно на второй орт, то по стрелке получим третий орт, причем взятый с «+», если поворот против часовой стрелки, и берется с «-», если по часовой стрелке.

i´j= k,

i´k= -j,

j´k= i,

j´i= -k,

i´i= 0.

---

Дата добавления: 2019-09-13; просмотров: 466; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!