Теорема о разложении вектора по базису.
Теорема. Любой вектор ЛП разлагается, причем единственным образом, в ЛК базисных векторов этого пространства.
Док-во: Рассмотрим ЛП размерности n с базисом l 1 , l 2 , ... , ln. Вектор а Є ЛП. Система векторов l 1 , l 2 , ... , ln , а содержит ( n +1) вектор, а пространство размерности n . Отсюда следует, что система ЛЗ, т.е. линейная комбинация
α1 l 1 + α2 l 2 + ... +α n ln +α n +1 a = 0, причем среди коэффициентов есть ≠ 0.
Покажем, что коэффициент α n +1 ≠ 0 от противного. Допустим, что α n +1 = 0. Тогда α1 l 1 + α2 l 2 + ... +α n ln +0 a = 0.
Отсюда следует, что α1 l 1 + α2 l 2 + ... +α n ln = 0 и есть ≠ 0 коэффициент.
Получили противоречие тому, что базис l 1 , l 2 , ... , ln – ЛНЗ.
Отсюда следует α n +1 ≠ 0.
Следовательно, мы доказали, что коэффициент α n +1 ≠ 0.
Разделим на коэффициент α n +1:

Отсюда следует, что вектор а - ЛК базисных векторов.
Докажем единственность разложения базиса от противного.
Пусть есть два разложения вектора а по базису.
a = α 1 l1+ α 2 l2+ ... + α n ln
a = β 1 l1+ β 2 l2+ ... + β n ln
0 = ( α 1 - β 1 ) l1+ ( α 2 - β 2 ) l2+ … + ( α n - β n ) ln.
Т.к. базис - ЛНЗ, то коэффициенты α 1 - β 1 =0, α 2 - β 2 =0, α n - β n =0.
Отсюда следует α1=β1, α2=β2 , α n =β n, т.е. коэффициенты совпали. Единственность разложения доказана.
Ч.т.д.
Координаты вектора в данном базисе. Операции с векторами в координатной форме.
Рассмотрим в ЛП размерности n базис l 1 , l 2 , ... , ln. Любой вектор ЛП разлагается в линейную комбинацию базиса х = α1 l 1 + α2 l 2 + ... +α n ln (по теореме о разложении по базису), х Є ЛП.
|
|
|
Определение: Упорядоченный набор чисел, участвующий в разложении вектора по базису (α1, α2,… α n ) называется координатами этого вектора в данном базисе.
х =(α1, α2,… α n ) – координаты вектора ЛП.
Операции:
1) Для того, чтобы сложить два вектора ЛП в координатной форме нужно сложить их соответствующие координаты.
Док-во: Возьмем два вектора ЛП.
| + |
у = (β1, β2, … β n )= β1 l 1 + β2 l 2 +…+β n ln
х + у = (α1 +β1, α2 +β2,… α n +β n ) = (α1 + β1) l 1 +(α2 + β2) l 2 +…+(α n +β n ) ln.
Ч.т.д.
2) Чтобы вектор в координатной форме умножить на число нужно каждую координату умножить на это число.
Док-во: х =(α1, α2,… α n )= α1 l 1 + α2 l 2 + ... +α n ln.
λ х = (λ1α1, λ2α2,… λ n α n )= λ1α1 l 1 + λ2α2 l 2 + … +λ n α n ln.
Ч.т.д.
Евклидово пространство.
Определение: Линейное пространство называется евклидовым, если в нем введена операция скалярного произведения, которая ставит в соответствие любым векторам х и у Є L число x • y, удовлетворяющее следующим свойствам:
1° x•y=y•x;
2° ( l x)• y= l (x•y);
|
|
|
3° x•(y + z)= x•y + x•z;
4° x • x ³ 0,причем скалярный квадрат x • x = 0 ↔ х= 0.
В Евклидовых пространствах можно ввести понятие длины вектора (модуль вектора)  и угол между векторами
и угол между векторами 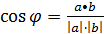 .
.
Нужно показать, что ïcos jï£ 1.
Для этого докажем неравенство Коши - Буняковского (Шварца):
0£│a • b│£│a│·│b│.
Док-во: Рассмотрим скалярный квадрат
( a - l b )•( a - l b )= a • a - l a • b - l a • b + l 2 b • b = │ a │2- 2 l a • b + l 2 │ b │2 ³ 0, как скалярный квадрат.
Последнее неравенство рассмотрим как квадратное относительно l.
l 2 │ b │2- 2λ a • b +│ a │2 ³ 0.
Чтобы это неравенство выполнялось при любом λ, нужно, чтобы дискриминант D £ 0.
D= b2- 4ac= (-2a•b)2- 4│b│2·│a│2 £ 0.
4(a•b) 2- 4│b│2·│a│2 £ 0 ê : 4;
(a•b) 2 £ │b│2·│a│2.
Извлекаем корень  :
:
0 £ │a • b│ £ │a│·│b│.
Ч.т.д.
На основании неравенства Коши - Буняковского определение косинуса угла между векторами Евклидова пространства корректно.
Замечание: Евклидово пространства размерности n принято обозначать En,
E2 - евклидово пространство всех векторов на плоскости, E3 - в пространстве.
Дата добавления: 2019-09-13; просмотров: 726; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
