Переход от одних уравнений прямой к другим.

1) От канонических к параметрическим.

.

  

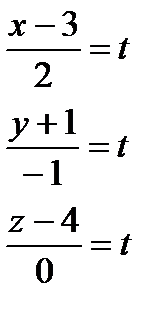
2) От параметрических к каноническим.

 

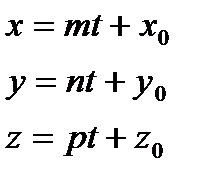
l= (2,-1,3), т. М₀= (-1,2,1).

.

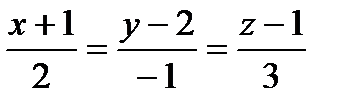3)От общих к каноническим.

2x - y + z - 3=0       N₁=(2, -1, 1),

x - 3y - z - 2=0             N₂= (1, -3, -1).

 

 l ^ N₁

 l ^ N₂ ,

l= N₁ ×N₂=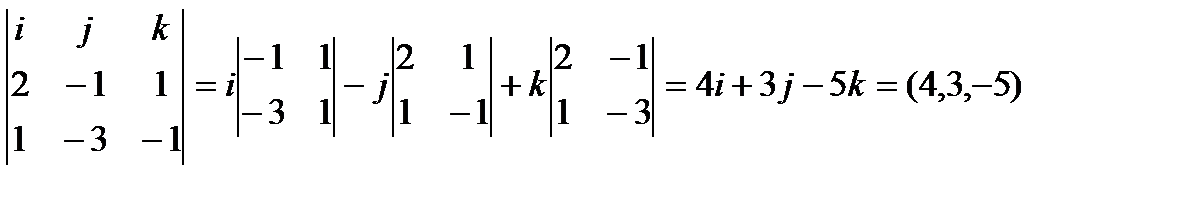

Пусть х=0, тогда -y + z - 3= 0 +

                         -3y - z - 2= 0

                         -4y – 5= 0

                            y= 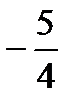 , z=

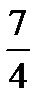
т. М₀= .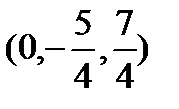

.

 

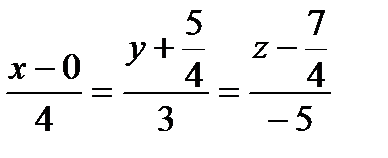Взаимное расположение прямых в пространстве.

1) Прямая (1) c направляющим вектором l ₁ = ( m ₁ , n ₁ , p ₁ ) ║ прямой (2) c направляющим вектором l ₂ =( m ₂ , n ₂ , p ₂ ).

l2

l1

1

2

 

l ₁ ║ l ₂. Отсюда следует, что 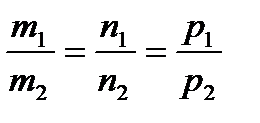 - условие параллельности двух прямых в пространстве.

 

2) Прямая (1) ^ прямой (2).

1

l2

l1

2

 

l ₁ ^ l ₂. Отсюда следует:  l ₁ • l ₂ =0.

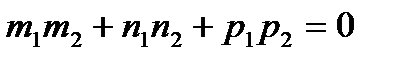 - условие перпендикулярности двух прямых в пространстве.

 

3) Угол между двумя прямыми - это угол между их направляющими векторами.

φ

l1

l2

2

1

 - угол между прямыми.

 

Взаимное расположение прямой и плоскости в пространстве.

Возьмем в пространстве плоскость α с уравнением ,

N = ( A , B , C ), и прямую а с уравнением 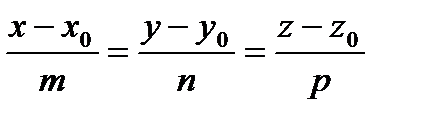, l = ( m ; n ; p ).

Возможны следующие случаи расположения:

1) Прямая ^ плоскости.

N ║ l: 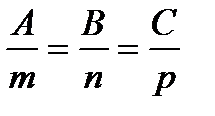 - условие перпендикулярности прямой и плоскости.

 

2) Прямая ║ плоскости.

N ^ l . N • l = 0: Am + Bn + Cp = 0 - условие параллельности прямой и плоскости.

 

3) Прямая лежит в плоскости.

N ^ l, т. М₀ на прямой Є плоскости.

N • l = 0, координаты т. М₀ удовлетворяют уравнению плоскости.

 - условие принадлежности прямой к плоскости.

 

4) Угол между прямой и плоскостью - это угол между прямой и ее проекцией на плоскость.

 ;    .

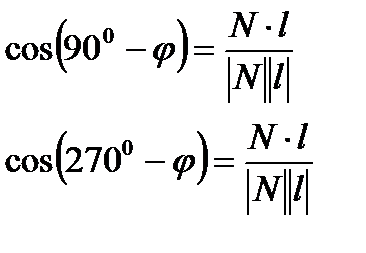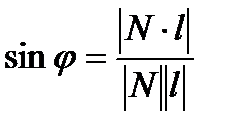- угол между прямой и плоскостью в пространстве.

Расстояния между различными объектами в пространстве.

1) Расстояние от точки до плоскости.

Найдем расстояние от т. М₀ (x₀, y₀, z₀) до плоскости Ax + By + Cz + D =0. Расстояние от точки до плоскости - это длина перпендикуляра, опущенного из точки на плоскость. Проведем через М₀ прямую, перпендикулярную плоскости. т. N₀ – точка пересечения прямой и плоскости.

.

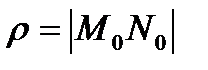а) Составим параметрические уравнения прямой:

l= N= (A, B, C) ║прямой,

т. М₀ (x₀, y₀, z₀) Є прямой.

x= At+ x₀

y= Bt+ y_0.

z= Ct+ z₀

б) т. N₀ – общая для прямой и плоскости, поэтому подставим параметрические уравнения прямой в уравнение плоскости и найдем параметр, соответствующий т. N₀:

A(At+ x₀) + B(Bt+ y₀) + C(Ct+ z₀) + D=0;

(A²+ B²+ C²)t+ Ax₀+ By₀+ Cz₀+ D=0;

,

координаты т. N₀ .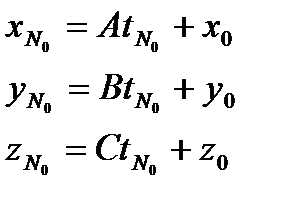

в)

 

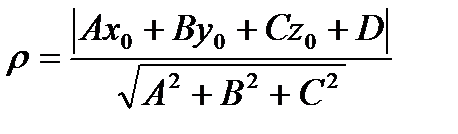 - расстояние от точки до плоскости.

 

2) Расстояние между двумя параллельными плоскостями.

На одной плоскости нужно взять произвольную точку и найти расстояние от этой точки до другой плоскости.

 

3) Расстояние между прямой и параллельной плоскостью.

На прямой нужно взять произвольную точку и найти расстояние от этой точки до плоскости.

а

α

4) Расстояние от точки до прямой.

т. М₀ (3, 1, -1), прямая .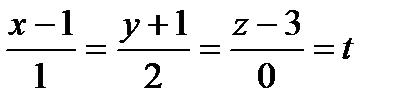

M0

N0

a

l

ρ

Проведем через т. М₀ плоскость, перпендикулярную прямой (проектирующая плоскость). Найдем точку пересечения прямой и плоскости.

.

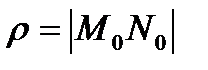а) Составим уравнение плоскости:

l = N = (1, 2, 0) ^ плоскости,

  т. М₀ (3, 1, -1) Є плоскости.

A(x- x₀) + B(y- y₀) + C(z- z₀)= 0,

1( x - 3) + 2( y - 1) + 0( z + 1)= 0,

x + 2 y - 5= 0 - уравнение плоскости.

б) Составим параметрические уравнения прямой:

x= t+ 1

y= 2t- 1

z= 0t- 3

в) т. N₀ – точка пересечения прямой и плоскости. Подставим параметрические уравнения прямой в уравнение плоскости.

(t+ 1)+ 2(2t- 1)- 5= 0, t+ 1+ 4t- 2- 5= 0, 5t- 6= 0, 5t= 6.

, т. N₀  

т. N_{0 .}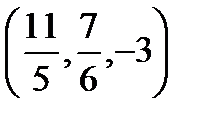

г)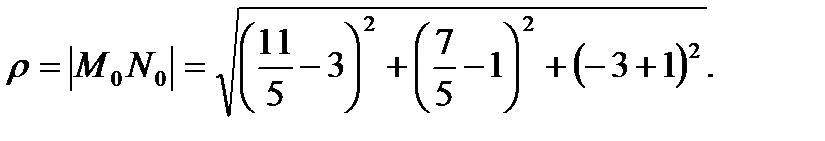

Прямая на плоскости.

Аналогично тому, как выводились канонические уравнения прямой в пространстве выводятся канонические уравнения прямой на плоскости.

М (х, у)

 

l=(m, n)

а

М0(х0, у0)

 

М₀М ║ l. Отсюда следует, что 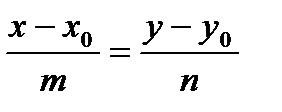 - каноническое уравнение прямой на плоскости, где l =( m , n ) - направляющий вектор прямой.

.

.

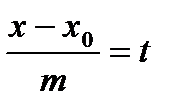
x = mt + x ₀

y = nt + y ₀  - параметрические уравнения прямой на плоскости.

M(x, y)

l

M2(x2, y2)

М1(x1, y1)

а

 

 

M ₁ M ║ M ₁ M ₂. Отсюда следует, что 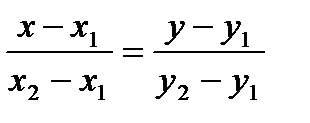 - уравнение прямой через две точки.

Если в каноническом уравнении 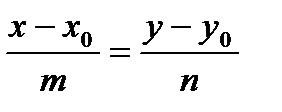 знаменатели m ≠0, n ≠0, то можно освободиться от знаменателей:

, , .

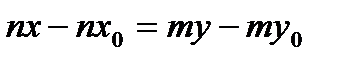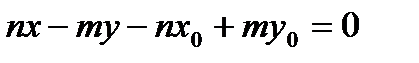 -общее уравнение прямой на плоскости.

N = ( A , B ) - нормаль, перпендикулярная прямой.

Проверка: N = ( A , B )= ( n , - m ), l = ( m , n ), N • l = m · n - n · m = 0.

⇒ N ^ l. Отсюда следует, что N ^ прямой.

l= (m, n)

N=(A, B)

 

 

Исследуем общее уравнение:

1) А=0, B и С≠ 0, т.е. нет х. Прямая параллельна ОХ.

 

 

0

x

у

а

 

                                

y= const - уравнение прямой параллельной оси ОХ.

2) В=0, А и С≠ 0, т.е. нет у. Прямая параллельна ОУ.

0

у

х

а

х= const - уравнение прямой параллельной оси ОУ.

3) С=0, А и В ≠ 0: Ах+Ву=0, т.е. т. О(0, 0) принадлежит прямой. Прямая проходит через начало координат.

у

0

х

а

4) у=0 - уравнение оси ОХ. х=0 - уравнение оси ОУ.

Пусть прямая отсекает на координатных осях отрезки: a - на оси ОХ и b - на оси ОУ.

A(a, 0)

В(0, b)

b

у

0

х

а

Прямая проходит через две точки A ( a , 0) и В(0, b ).

Уравнение: .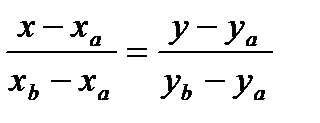

, ,

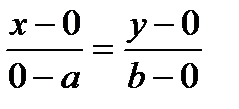b ( x - a )= - ay , bx - ab + ay =0, bx + ay - ab =0, bx + ay = ab │: ab ,

 - уравнение прямой в отрезках.

Если в каноническом уравнении 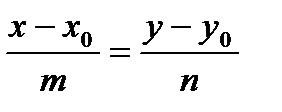, m ≠ 0, то выразим у:

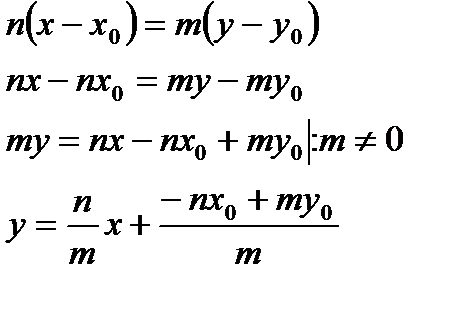
- уравнение прямой с угловым коэффициентом ( k ).

Выясним смысл k и b.

Из треугольника: tg α= 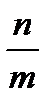, tg α= k.

Угловой коэффициент прямой равен тангенсу угла наклона прямой к положительному направлению оси ОХ.

Так как y (0)= b, то b - отрезок, отсекаемой прямой на оси ОУ.

Через любую точку плоскости проходит бесконечное множество прямых.

Такое множество прямых, проходящих через точку, называется пучком прямых.

 

Уравнение пучка прямых: .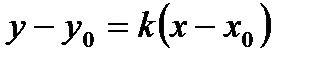

Задавая различные значения угловых коэффициентов k можно выбирать различные прямые из пучка.

Пример. Вывести формулу для вычисления расстояния от точки до прямой .

 

---

Дата добавления: 2019-09-13; просмотров: 494; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!