Размерность и базис линейного пространства.
Министерство образования и науки российской федерации
Федеральное государственное автономное образовательное учреждение
высшего профессионального образования
«Национальный исследовательский ядерный университет «МИФИ»
Волгодонский инженерно-технический институт - филиал НИЯУ МИФИ
КУРС ЛЕКЦИЙ
По дисциплине «Линейная алгебра. Аналитическая геометрия. Начала анализа» 1 семестр
Для студентов очной формы обучения
Раздел №1,2 «Элементы линейной, векторной алгебры и аналитической геометрии»
Волгодонск
Линейные (векторные) пространства.
Определение: Множество L называется линейным (векторным) пространством, если на нем введены две операции:
1) сложение: для любых х, у Є L сумма (х + у) Є L,
2) умножение на число: для любого х Є L и любого числа λ произведение
λх Є L,
которые удовлетворяют 8 аксиомам:
1) х + у = у + х, где х,у Є L ;
2) (х + у)+ z = x +(у + z ), где х,у, z Є L ;
3) существует нулевой элемент Ө такой, что Ө + х = х, где х Є L ;
4) для любого х Є L существует единственный противоположный элемент
(–х) такой, что х + (-х)= Ө;
5) 1·х = х, где х Є L ;
6) α(βх) = (αβ)х, где х Є L, α и β- числа;
7) α(х + у) = αх + αу, где х,у Є L, α- число;
8) (α + β) х = αх + βх, где х Є L, α и β- числа.
Замечание: Элементы линейного (векторного) пространства называют векторами.
Примеры:
Множество действительных чисел является линейным пространством.
|
|
|
Множества всех векторов на плоскости и в пространстве являются линейным пространством.
Множество всех матриц одного размера является линейным пространством.
Линейная зависимость и независимость векторов линейного пространства.
Дана в линейном пространстве система векторов а1, а2, а3, … а n Є L.
Определение: Вектор α1 а1+ α2 а2+…+ α n а n Є L, где α i (i = 1,…,n) - числа, называется линейной комбинацией (ЛК) векторов а1, а2, а3, … а n.
Определение: Система векторов линейного пространства а1, а2, а3, … а n Є L называется линейно независимой (ЛНЗ), если линейная комбинация
α1 а1+ α2 а2+α3 а3+…+ α n а n =0 тогда и только тогда, когда коэффициенты
α 1 =α 2 =α 3 =…=α n =0.
Определение: Система векторов а1, а2, а3, … а n Є L называется линейно зависимой (ЛЗ), если существует набор чисел α1, α2 ,α3 … α n, не все из которых равны 0, такие что линейная комбинация α1 а1+ α2 а2+…+ α n а n = 0.
Примеры:
Два вектора называются коллинеарными, если они параллельны одной прямой или лежат на одной прямой.
1) Рассмотрим два ненулевых, неколлинеарных вектора на плоскости. Диагональ 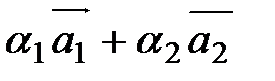 =0
=0 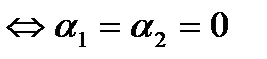 .
.
| α2а2 |
| α1а1+α2а2 |
а1 α1 а1
|
|
|
Два ненулевых, не коллинеарных вектора на плоскости линейно независимы.
2) Рассмотрим два ненулевых , коллинеарных вектора а1 ║а2.
| а1 |
| а2 |
Линейная комбинация равна нулю, есть не нулевой коэффициент, следовательно, два коллинеарных вектора на плоскости линейно зависимы.
Теоремы о линейно зависимых системах векторов линейного пространства.
Теорема 1. Необходимое и достаточное условие линейной зависимости.
Для того чтобы система векторов линейного пространства была линейно зависимой необходимо и достаточно, чтобы какой-нибудь вектор этой системы был линейной комбинацией всех остальных.
Док-во: Необходимость ( ).
Дана ЛЗ система. Нужно доказать, что один вектор ЛК всех остальных.
а1, а2, а3, … а n – ЛЗ система векторов, т.е. среди α1, α2 ,α3 … αn существует число отличное от нуля так, что ЛК α1 а1+ α2 а2+α3 а3+…+ α n а n = 0.
Положим для определения, что коэффициент α1 ≠ 0. Разделим обе части последнего равенства на α1 ≠ 0:
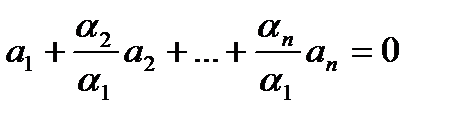 ;
;
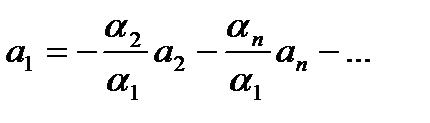 .
.
Отсюда следует, что а1 - ЛК остальных векторов.
Необходимость доказана.
Достаточность ( ).
Пусть один вектор – это линейная комбинация остальных. Нужно доказать, что система векторов ЛЗ.
|
|
|
Пусть α n = α1 а1+ α2 а2+α3 а3+…+ α n -1 а n -1.
α1 а1+ α2 а2+α3 а3+…+ α n -1 а n -1 - 1α n = 0.
Так как есть не нулевой коэффициент, то система векторов а1, а2, а3, … а n- линейно зависима.
Ч.т.д.
Теорема 2. Система, содержащая нуль-вектор, линейна зависима.
Док-во: Рассмотрим систему векторов, содержащую нуль-вектор. а1, а2, а3, … а n ,Ө, где Ө ‒ нуль-вектор. Очевидно, что имеет место следующее равенство 0·а1+ 0· а2+0· а3+…+ 5·Ө = 0.
Есть не равный нулю коэффициент, равный 5, а линейная комбинация равна 0, отсюда следует, что система векторов ЛЗ.
Ч.т.д.
Теорема 3. Система, содержащая линейно зависимую подсистему, тоже будет линейно зависима.
Док-во: Рассмотрим систему векторов а1, а2, …,ак, ак+1 … а n, где а1, а2,…, ак - линейно зависимый кусочек. α1 а1+ α2 а2+ … +αкак= 0. Есть коэффициент отличный от нуля.
Очевидно, что с этими же коэффициентами будет выполняться равенство
α1 а1+ α2 а2+…+αк ак+…+0· ак+1+…+ 0·α n = 0.
Отсюда следует, что система векторов ЛЗ.
Ч.т.д.
Размерность и базис линейного пространства.
Определение: Если в ЛП система, состоящая из n векторов ЛНЗ, а любая система с большим количеством векторов ЛЗ, то такое пространство называется n - мерным, а n называют размерностью пространства.
|
|
|
Другими словами, размерность ЛП - это максимальное количество ЛНЗ векторов, помещающихся в этом пространстве.
Определение: Любые n ЛНЗ векторов ЛП размерности n l 1 , l 2 , ... , ln называются базисом ЛП.
Примеры:
1) Любой ненулевой вектор на прямой ЛНЗ и является базисом ЛП всех векторов на прямой.
2) Любые два ненулевых не коллинеарных вектора на плоскости ЛНЗ (любые три вектора на плоскости будут ЛЗ) и образуют базис ЛП всех векторов на плоскости.
3) Можно показать, что любые 3 ненулевых и некомпланарных вектора в пространстве ЛНЗ (любые 4 вектора ЛЗ) и образуют базис ЛП всех векторов в пространстве.
Определение: Три вектора А, В, С ‒ компланарны, если они параллельны одной плоскости или лежат в одной плоскости.
Дата добавления: 2019-09-13; просмотров: 196; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
