Уравнение плоскости, проходящей через 3 точки.
Аксиома: Через три точки, не лежащие на одной прямой, проходит единственная плоскость.
Пусть т. М1( x 1 , y 1 , z 1 ), т. М2 ( x 2 , y 2 , z 2 ), т. М3( x 3 , y 3 , z 3 ) Є плоскости.
Пусть т. М ( x , y , z ) - текущая точка плоскости.
| M |
| М1 |
| М2 |
| М3 |
Вектор М 1 М = ( х - x1, y- y1, z- z1), М 1 М 2 = (x2 - x1, y2 - y1, z2 - z1),
М1М3= ( x 3 - x 1 , y 3 - y 1 , z 3 - z 1 ).
Все вектора лежат в одной плоскости ⇒ векторы компланарны. Тогда смешанное произведение векторов М1М·М1М2· М1М3= 0:
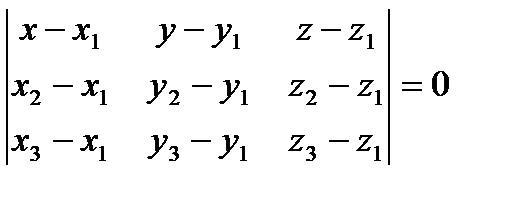- уравнение плоскости через три точки.
Уравнение плоскости в отрезках.
Пусть плоскость отсекает на координатных осях отрезки a – на оси ОХ, b – на оси ОУ, с – на оси OZ.
Тогда т. А (а, 0, 0), т. В (0, b, 0), т. C (0, 0, c) Є плоскости.
Тогда вектора AM ( x - a , y , z ), AB (- a , b , 0), AC (- a , 0, c ) компланарны. Отсюда следует, что AM · AB · AC = 0.
.
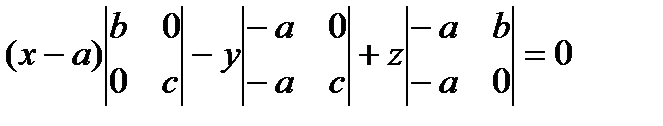
bc (x-a)+ acy+ abz= 0,
bcx+ acy+ abz= bac │: abc,
- уравнение плоскости в отрезках.
Взаимное расположение двух плоскостей.
1) Плоскость (1) с уравнением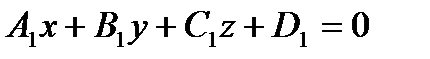 
параллельна плоскости (2) с уравнением 
.
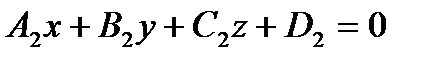Отсюда следует, что 
║ 
. Координаты коллинеарных векторов пропорциональны.
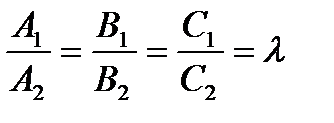- условие параллельности двух плоскостей.
Если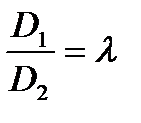 
, то такие плоскости будут совпадать.
2) Плоскость (1) перпендикулярна плоскости (2).
⇒ ^ . Отсюда следует, что скалярное произведение • =0. 
- условие перпендикулярности двух плоскостей.
3) При пересечении двух плоскостей образуются две пары двухгранных углов.
Углом между двумя плоскостями считают угол между их векторами нормали: 
- угол между плоскостями.
|
|
|
Прямая в пространстве.
Определение: Любой ненулевой вектор, параллельный прямой, называется направляющим вектором этой прямой.
l = ( m ; n ; p ) ║прямой.
Пусть т. М0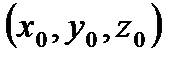 
- произвольная фиксированная точка прямой,
т. М 
- текущая фиксированная точка прямой.
Вектор М0М=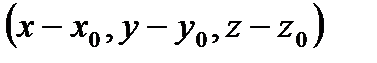 
║ l = ( m ; n ; p ).
Координаты векторов М0М и l пропорциональны.
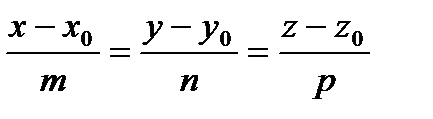- каноническое уравнение прямой в пространстве.
Положим в канонических уравнениях все равно параметру t и выразим x , y , z :
.
; 
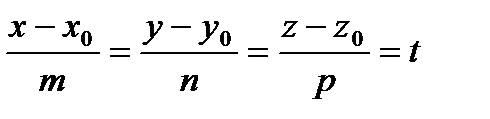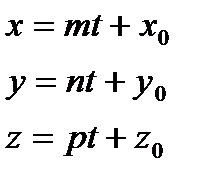- параметрические уравнения прямой в пространстве.
Задавая различные значения параметра t из параметрических уравнений можно получать точки, принадлежащие прямой.
Аксиома: Через две различные точки проходит одна прямая.
| a |
| M(x, y, z) |
| M2(x2, y2, z2) |
| M1(x1, y1,z1) |
| l |
Прямая а проходит через М1, М2. М1М и М1М2 – направляющие векторы.
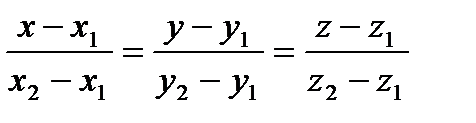- уравнение прямой, проходящей через две точки.
Общее уравнение прямой в пространстве.
Прямая может быть задана в пространстве как линия пересечения плоскостей:
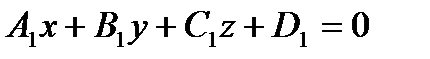
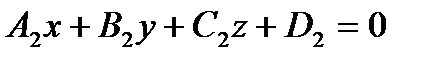- общее уравнение прямой в пространстве.
Замечание: такое задание прямой неоднозначно.
Для нахождения направляющего вектора прямой, нужно провести следующие рассуждения:
|
|
|
l ^ N 1
l ^ N 2 l = N 1 × N 2 .
Для нахождения точки, принадлежащей прямой, нужно в общих уравнениях одну координату обнулить, например, положить х=0 и вычислить из системы у,z. Если известен, направляющий вектор прямой и точка, принадлежащая прямой, то такая прямая называется заданной, т.е. можно составить ее каноническое уравнение.
Дата добавления: 2019-09-13; просмотров: 177; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!