Проверка статистической значимости коэффициентов регрессии
Надежность получаемых оценок 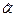 и
и  зависит, очевидно, от их дисперсий, которые вычисляются по следующей формуле
зависит, очевидно, от их дисперсий, которые вычисляются по следующей формуле
 ,
,  , где
, где  и представляет собой оценку дисперсии случайных отклонений
и представляет собой оценку дисперсии случайных отклонений  .
.
Проверка значимости отдельных коэффициентов регрессии связана с определением расчетных значений t-критерия (t–статистики) для соответствующих коэффициентов регрессии:
 ,
, 
Затем эти расчетные значения сравниваются с табличными t табл. Табличное значение критерия определяется при (n-2) степенях свободы (n - число наблюдений) и соответствующем уровне значимости a (0,01; 0,05)
Если расчетное значение t-критерия с (n-2) степенями свободы по модулю превосходит его табличное значение при заданном уровне значимости, то оценка коэффициента регрессии считается значимой. В противном случае оценка коэффициента регрессии является незначимой и фактор, соответствующий этой оценке, следует исключить из модели (при этом ее качество не ухудшится).
Пример 2.2. Используя данные примера 2.1, проверить статистическую значимость оценки параметра  на 5% уровне (
на 5% уровне (  .
.
Решение. Величину отклонения от линии регрессии вычисляют по формуле  (таблица 2.2), используя данные таблицы 2.1.
(таблица 2.2), используя данные таблицы 2.1.
Таблица 2.2.
| Наблюдение | y | 
| 
| 
|
| 1 | 3 | 3.541 | -0.5406 | 0.2923 |
| 2 | 6 | 5.688 | 0.3125 | 0.0977 |
| 3 | 5 | 4.256 | 0.7438 | 0.5532 |
| 4 | 3.5 | 2.109 | 1.3906 | 1.9338 |
| 5 | 1.5 | 2.109 | -0.6094 | 0.3713 |
| 6 | 4.5 | 4.972 | -0.4719 | 0.2227 |
| 7 | 2 | 2.825 | -0.8250 | 0.6806 |
| Сумма | 25.5 | 25.500 | 0.0000 | 4.1516 |
|
|
|
Тогда
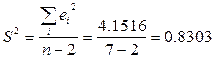 ,
,
 ,
,  ,
,
 .
.
Табличное значение статистики Стьюдента 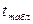 для m =5 степеней свободы ( m = n -2) и уровня значимости 0.05 равно 2,571 (см. Приложение, таблица 1). Как видим
для m =5 степеней свободы ( m = n -2) и уровня значимости 0.05 равно 2,571 (см. Приложение, таблица 1). Как видим  по модулю превосходит
по модулю превосходит  =2,571, следовательно, оценка параметра
=2,571, следовательно, оценка параметра  является статистически значимой.
является статистически значимой.
Раздел 3. Модель множественной линейной регрессии
Значения экономических переменных определяются обычно влиянием не одного, а нескольких объясняющих факторов. Предположим, что модель наблюдений имеет вид
 где
где
 - значение объясняемой переменной в
- значение объясняемой переменной в  -м наблюдении;
-м наблюдении;
 - известное значение
- известное значение  -ой объясняющей переменной в
-ой объясняющей переменной в  -м наблюдении;
-м наблюдении;
 - неизвестный параметр при
- неизвестный параметр при  -ой объясняющей переменной;
-ой объясняющей переменной;
 - случайная составляющая (“отклонений“) в
- случайная составляющая (“отклонений“) в  -ом наблюдении.
-ом наблюдении.
Предполагается, чтослучайные величины  независимы в совокупности, имеют одинаковое нормальное распределение с нулевым математическим ожиданием и однородной дисперсией
независимы в совокупности, имеют одинаковое нормальное распределение с нулевым математическим ожиданием и однородной дисперсией  (выполняются условия Гаусса-Маркова).
(выполняются условия Гаусса-Маркова).
Определенную указанным образом модель наблюдений мы будем называть нормальной линейной моделью множественной регрессии переменной y на переменные x1, ... , xp. Оцениваниенеизвестных параметров модели (  ) методом наименьших квадратов, как и в случае парной линейной регрессии,состоит в минимизации суммы квадратов отклонений, т. е. в минимизации следующей функции от параметров:
) методом наименьших квадратов, как и в случае парной линейной регрессии,состоит в минимизации суммы квадратов отклонений, т. е. в минимизации следующей функции от параметров:
|
|
|

Минимум этой суммы достигается при некотором наборе значений коэффициентов
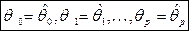 .
.
Решение данной задачи удобнее записать в матричном виде. Для этого введем следующие обозначения:

- матрица значений 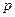 объясняющих переменных в
объясняющих переменных в  наблюдениях,
наблюдениях,
 ,
,  ,
, 
Тогда, в матричной форме решение выглядит следующим образом:

Качество модели регрессии оценивается по следующим направлениям:
1) проверка качества всего уравнения регрессии;
2) проверка значимости всего уравнения регрессии;
3) проверка статистической значимости коэффициентов уравнения регрессии;
Для оценки качества модели множественной регрессии вычисляют коэффициент детерминации  (формула 2.4, где
(формула 2.4, где  ). Чем ближе к 1 значение этих характеристик, тем выше качество модели.
). Чем ближе к 1 значение этих характеристик, тем выше качество модели.
Для проверки значимости модели регрессии используется  -критерий Фишера с
-критерий Фишера с  степенями свободы, вычисляемый по формуле:
степенями свободы, вычисляемый по формуле:
 , где
, где  - число объясняющих факторов,
- число объясняющих факторов,  - объем выборки. Если расчетное значение больше табличного при заданном уровне значимости (см. Приложении, таблица 2), то модель считается значимой.
- объем выборки. Если расчетное значение больше табличного при заданном уровне значимости (см. Приложении, таблица 2), то модель считается значимой.
|
|
|
Распределение Фишера может быть использовано не только для проверки гипотезы об одновременном равенстве нулю всех коэффициентов линейной регрессии (значимости модели), но и гипотезы о равенстве нулю части этих коэффициентов. Это особенно важно при развитии линейной регрессионной модели, так как позволяет оценить обоснованность исключения отдельных переменных или их групп из числа объясняющих переменных, или же, наоборот, включения их в это число.
Пусть, например, вначале была оценена множественная линейная регрессия

по п наблюдениям с 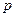 объясняющими переменными, и коэффициент детерминации равен
объясняющими переменными, и коэффициент детерминации равен  . Затем последние к переменных исключены из числа объясняющих, и по тем же данным оценено уравнение
. Затем последние к переменных исключены из числа объясняющих, и по тем же данным оценено уравнение
 ,
,
для которого коэффициент детерминации равен  (он обязательно уменьшился, поскольку каждая дополнительная переменная объясняет часть, пусть небольшую, вариации зависимой переменной). Для того чтобы проверить гипотезу об одновременном равенстве нулю всех коэффициентов регрессии при исключенных переменных рассчитывается величина
(он обязательно уменьшился, поскольку каждая дополнительная переменная объясняет часть, пусть небольшую, вариации зависимой переменной). Для того чтобы проверить гипотезу об одновременном равенстве нулю всех коэффициентов регрессии при исключенных переменных рассчитывается величина
 , (3.1)
, (3.1)
имеющая распределение Фишера с 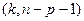 степенями свободы. По таблицам, при заданном уровне значимости, находится критическое значение
степенями свободы. По таблицам, при заданном уровне значимости, находится критическое значение  -статистики (см. Приложение, таблица 2), и если ее рассчитанное значение превосходит критическое, то нулевая гипотеза отвергается. В таком случае исключать сразу из числа объясняющих все
-статистики (см. Приложение, таблица 2), и если ее рассчитанное значение превосходит критическое, то нулевая гипотеза отвергается. В таком случае исключать сразу из числа объясняющих все  переменных некорректно.
переменных некорректно.
|
|
|
Пример 3.1. По  наблюдениям построено уравнение линейной регрессии, содержащее
наблюдениям построено уравнение линейной регрессии, содержащее  фактора. Для этой модели коэффициент детерминации
фактора. Для этой модели коэффициент детерминации  . После этого из модели исключили
. После этого из модели исключили  фактор. Для нового уравнения линейной регрессии коэффициент детерминации
фактор. Для нового уравнения линейной регрессии коэффициент детерминации  . Существенно ли ухудшилось качество описания поведения результативного признака
. Существенно ли ухудшилось качество описания поведения результативного признака  ? Уровень значимости
? Уровень значимости 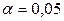 .
.
Решение. Из таблиц  -распределения (см. Приложение, таблица 2) находим граничную точку
-распределения (см. Приложение, таблица 2) находим граничную точку  -статистики с числом степеней свободы равном
-статистики с числом степеней свободы равном 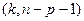 =(1,10):
=(1,10):  . Воспользовавшись формулой 3.1, найдем значение
. Воспользовавшись формулой 3.1, найдем значение  -статистики:
-статистики:
 .
.
Как видно, данное значение превышает табличное и, следовательно, гипотеза о равенстве нулю коэффициента при исключенной переменной отвергается. Таким образом, качество описания поведения результативного признака  ухудшилось существенно.
ухудшилось существенно.
Для анализа статистической значимости оценок параметров множественной линейной регрессии необходимо, как и в случае парной регрессии, необходимо вычислить их дисперсии, для которых получены следующие выражения:
 ,
,
где  - диагональный элемент матрицы
- диагональный элемент матрицы  . Оценка
. Оценка  признается статистически значимой при выбранном уровне значимости
признается статистически значимой при выбранном уровне значимости  , если статистика Стьюдента с
, если статистика Стьюдента с 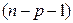 степенями свободы, вычисленная по формуле
степенями свободы, вычисленная по формуле  по модулю превосходит
по модулю превосходит 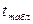 .
.
Мультиколлинеарность.
Для множественной регрессии существует так называемая проблема мультиколлинеарности. Мультиколлинеарность - это коррелированность двух или нескольких объясняющих переменных в уравнении регрессии. Оценка коэффициента регрессии может оказаться незначимой не только из-за несущественности данного фактора, но и из-за того, что трудно разграничить воздействие на зависимую переменную двух или нескольких факторов. Это бывает в том случае, когда какие-то факторы линейно связаны между собой (коррелированы) и меняются синхронно. Связь зависимой переменной с изменениями каждого из них можно определить, только если в число объясняющих переменных включается лишь один из этих факторов. Природа мультиколлинеарности нагляднее всего может быть продемонстрирована на примере совершенной мультиколлинеарности, то есть строгой линейной связи между объясняющими переменными. Например, если в уравнении

объясняющие переменные  и
и  связаны линейным соотношением
связаны линейным соотношением  , то исходное уравнение сводится к уравнению простой линейной регрессии
, то исходное уравнение сводится к уравнению простой линейной регрессии
 ,
,
в котором могут быть получены оценки коэффициентов  и
и  . Последнее уравнение представляет собой одно уравнение с двумя неизвестными
. Последнее уравнение представляет собой одно уравнение с двумя неизвестными 
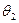 , которые найдены пo отдельности, естественно быть не могут. Таким образом, совершенная мультиколлинеарность не позволяет определить коэффициенты регрессии и разделить вклады переменных
, которые найдены пo отдельности, естественно быть не могут. Таким образом, совершенная мультиколлинеарность не позволяет определить коэффициенты регрессии и разделить вклады переменных  и
и  в объяснение поведения переменной у. Несовершенная мультиколлинеарность, то есть стохастическая связь переменных
в объяснение поведения переменной у. Несовершенная мультиколлинеарность, то есть стохастическая связь переменных  и
и  , характеризуется величиной коэффициента корреляции между ними. Чем ближе пo абсолютной величине значение коэффициента корреляции к единице, тем ближе мультиколлинеарность к совершенной и тем труднее разделить влияния объясняющих переменных
, характеризуется величиной коэффициента корреляции между ними. Чем ближе пo абсолютной величине значение коэффициента корреляции к единице, тем ближе мультиколлинеарность к совершенной и тем труднее разделить влияния объясняющих переменных  и
и  на поведение переменной
на поведение переменной  и тем менее надежными будут оценки коэффициентов регрессии при этих переменных.
и тем менее надежными будут оценки коэффициентов регрессии при этих переменных.
В общем случае, если при оценке уравнения регрессии несколько факторов оказались незначимыми, то нужно выяснить, нет лисреди них сильно коррелированных между собой. Для этого распечатывается корреляционная матрица (это предусмотрено стандартными статистическими программными пакетами), и проверяется статистическая значимость коэффициентов парной корреляции. При наличии корреляции один из пары связанных между собой факторов исключается, либо в качестве объясняющего фактора берется какая-то их функция. Если же незначимым оказался только один фактор, то можно его исключить или заменить другим.
Дата добавления: 2019-09-02; просмотров: 1336; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
