Влияние постоянной силы на свободные незатухающие колебания
Пусть кроме восстанавливающей силы (2.1) на точку действует постоянная по модулю и направлению сила, например, сила тяжести. Для наглядности рассмотрим колебания груза, прикрепленного к концу пружины (Рис.2.3). На груз действуют две силы: сила тяжести и реакция пружины, величина которой пропорциональна удлинению пружины: 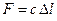 .
.
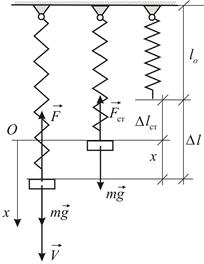
|
| Рис. 2.3 |
Выберем начало отсчета в положении статического равновесия  ; ось
; ось  направим вертикально вниз. Тогда
направим вертикально вниз. Тогда 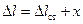 . Дифференциальное уравнение движения точки принимает вид:
. Дифференциальное уравнение движения точки принимает вид:
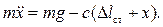 (2.16)
(2.16)
Учитывая условие статического равновесия: 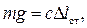 приводим уравнение (2.16) к виду:
приводим уравнение (2.16) к виду:
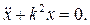 (2.18)
(2.18)
Таким образом, наличие постоянной силы не изменяет характера движения – оно остается простым гармоническим колебанием. Действие постоянной силы приводит только к тому, что центр колебаний смещается в сторону действия постоянной силы.
Движение точки при наличии сопротивления
Пусть кроме восстанавливающей силы на точку действует сила сопротивления, пропорциональная первой степени скорости. Дифференциальное уравнение движения
|
| Рис. 2.4 |
принимает вид:
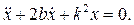 (2.19)
(2.19)
Рассмотрим возможные случаи.
|
|
|
Случай малого сопротивления 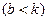 . Решение уравнения (2.19)представляется в виде:
. Решение уравнения (2.19)представляется в виде:
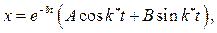 (2.20)
(2.20)
где
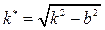
или в виде:
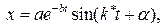 (2.21)
(2.21)
где 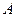 и
и 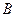 или
или 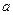 и
и 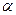 — постоянные интегрирования, определяемые из начальных условий.
— постоянные интегрирования, определяемые из начальных условий.
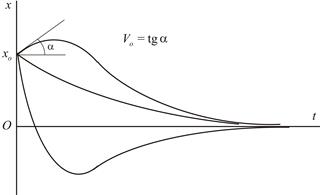
Как видно из решения (2.21), рассматриваемое движение будет затухающим колебанием, поскольку благодаря наличию множителя 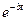 размахи колебаний будут со временем убывать, стремясь к нулю (Рис.2.4).
размахи колебаний будут со временем убывать, стремясь к нулю (Рис.2.4).
Случай большого сопротивления 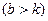 . Обозначая
. Обозначая 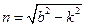 , получаем общее
, получаем общее
|
| Рис. 2.5 |
решение уравнения (2.19) в виде:
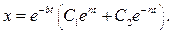
Как видно, колебаний в рассматриваемом случае не будет. Поскольку 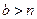 , с течением времени
, с течением времени 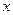 убывает, стремясь к нулю, т.е. точка со временем асимптотически приближается к положению равновесия. Примерный характер движения показан на Рис.2.5.
убывает, стремясь к нулю, т.е. точка со временем асимптотически приближается к положению равновесия. Примерный характер движения показан на Рис.2.5.
Граничный случай 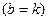 . Общее решение уравнения (2.19) имеет вид:
. Общее решение уравнения (2.19) имеет вид:
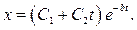 (2.23)
(2.23)
Картина движения в этом случае будет качественно такой же, как в случае большого сопротивления (Рис.2.5).
|
|
|
Вынужденные колебания при отсутствии сопротивления
Пусть на точку с массой 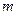 кроме восстанавливающей силы действует возмущающая сила вида (2.4). Влияние силы сопротивления мы рассмотрим в следующем параграфе. Дифференциальное уравнение движения имеет вид:
кроме восстанавливающей силы действует возмущающая сила вида (2.4). Влияние силы сопротивления мы рассмотрим в следующем параграфе. Дифференциальное уравнение движения имеет вид:
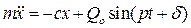 или
или 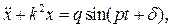 (2.24)
(2.24)
где
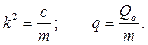
Общее решение неоднородного уравнения (2.24), как известно, складывается из общего решения соответствующего однородного уравнения (2.8) и любого частного решения 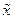 уравнения (2.24). Частное решение
уравнения (2.24). Частное решение 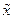 будем искать в виде:
будем искать в виде:
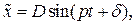 (2.25)
(2.25)
где 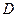 – любое число.
– любое число.
Подставляя предполагаемый вид решения (2.25) в уравнение (2.24), получаем:
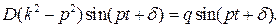
Как видно, функция (2.25) действительно будет решением уравнения (2.24), если
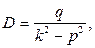
что возможно только при 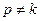 .
.
Таким образом, если 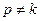 , общее решение уравнения (2.24) имеет вид:
, общее решение уравнения (2.24) имеет вид:
|
| Рис. 2.6 |
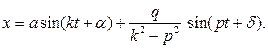 (2.26)
(2.26)
|
|
|
Как следует из полученного решения, движение точки в рассматриваемом случае представляет собой результат наложения двух колебаний: собственных с частотой 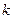 , амплитуда
, амплитуда 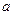 и начальная фаза
и начальная фаза 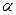 которых определяются начальными условиями, и вынужденных с частотой
которых определяются начальными условиями, и вынужденных с частотой 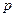 , равной частоте возмущающей силы. Амплитуда вынужденных колебаний от начальных условий не зависит.
, равной частоте возмущающей силы. Амплитуда вынужденных колебаний от начальных условий не зависит.
Если частота возмущающей силы равна частоте собственных колебаний, т.е., если  , то рассмотренное частное решение не имеет смысла. Рассмотрим другое частное решение, которое получается из общего решения (2.26) при конкретных значениях произвольных постоянных.
, то рассмотренное частное решение не имеет смысла. Рассмотрим другое частное решение, которое получается из общего решения (2.26) при конкретных значениях произвольных постоянных.
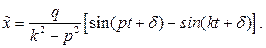 (2.27)
(2.27)
При 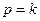 это частное решение имеет неопределенность вида
это частное решение имеет неопределенность вида 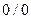 , раскрывая которую (по правилу Лопиталя), находим:
, раскрывая которую (по правилу Лопиталя), находим:
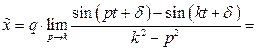
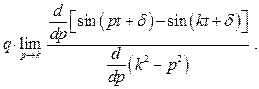
результате получаем:
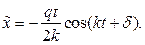 (2.28)
(2.28)
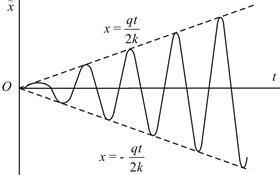
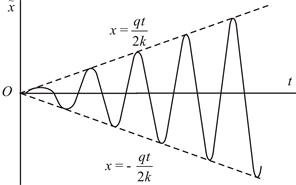
Как видно, в том случае, когда частота возмущающей силы совпадает с собственной частотой, амплитуда вынужденных колебаний с течением времени неограниченно возрастает (Рис.10.6). Такое явление называется резонансом. Резонанс играет важнейшую роль в акустике, радиотехнике, динамическом расчете сооружений и т.д.
|
|
|
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
- Что называется восстанавливающей силой?
- Что называется амплитудой, частотой и периодом свободных незатухающих колебаний?
- При каких условиях возникают свободные затухающие колебания?
- При каких условиях возникает апериодическое движение?
- Что называется резонансом и когда он возникает?
ЛЕКЦИЯ 3 (11)
ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
Дата добавления: 2019-09-02; просмотров: 221; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
