Механизм и схемы напряженно-деформированного состояния при раздаче
Рассмотрим обобщенный механизм способа раздачи на конической оправке.
ab – участок упругого деформирования, передающий основное усилие,
bc – участок радиуса свободного изгиба,
cd – основной участок пластической деформации,
de – участок закругления по радиусу оправки,
ef – упругий участок.
Всегда необходимо, чтобы 
. Если 
, то заготовка будет отходить от оправки.
Рассмотрим схемы напряженно-деформированного состояния.
Для участков bc, dc, de схема напряженно-деформированного состояния – одинаковая, но величины напряжений и деформаций – разные.
При раздаче нужно учитывать, чтобы 
, где 
- радиус оправки, 
.
Если данное условие не выполняется, то получаем следующее условие формообразования:
Если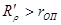 
, то заготовка отходит от оправки.
,
.
Чтобы этого избежать следует напряжение 
, либо производить формирование по матрице.
График изменения усилия при раздаче имеет следующий вид
АВ – участок неустановившегося деформирования,
Bh – участок установившегося деформирования.
Они отличаются тем, что на участке АВ для каждого элемента соотношение напряжений 
, а для участка Bh 
.
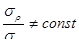Определение напряжений и деформаций при раздаче
Наиболее просто напряжения и деформации определяются для кромки заготовки
,
,
тангенсальная деформация 
.
Так как 
, то 
.
Если считать, что кромка деформируется как модель, близка к линейному растяжению, то для изотропного металла имеет место соотношение следующее соотношение дефомаций
.
– конечная величина.
.
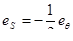Чтобы определить деформацию для других элементов, используем уравнение связи напряжений и деформаций.
. (*)
Данное уравнение получено из следующего: для монотонного процесса( для немонотонного используют скорости деформаций) имеем:
,
.
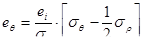Перепишем уравнение (*) в следующем виде:
.
Данное уравнение дает возможность определить деформации любого элемента для случая
1. если процесс монотонный, то есть все время происходит либо увеличение, либо уменьшение размеров;
2. когда известна одна из деформаций, например из геометрических соотношений;
3. Соотношение напряжений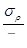 
находится из условия упрочнения и трения, также как при вытяжке.
Тангенсальную деформацию при раздаче находим из геометрических соотношений. Независимо от того, какой элемент мы рассматриваем с координатой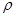 
– этот элемент имеет длину 
. Поэтому для любого элемента мы находим
.
Далее определим соотношение напряжений для идеального случая без учета трения, упрочнения, изменения толщины.
Для этот используем инженерный метод, решая уравнение равновесия.
Выделим бесконечно малый элемент.
Бесконечно малый элемент находится в равновесии силы, моментов или работы. Так как задача статическая, то мы рассматриваем условие равновесия сил. Находится условие равновесия сил по всем взаимно перпендикулярным осям: 
, 
, 
.
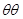В виду симметрии сумма сил на ось 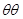обращается в тождество 
, 
.
Аналогично сумма сил на ось обращается в тождество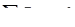 
, .
Составим уравнение равновесия на ось
,
,
здесь 
,
(где S-толщина),
,
,
.
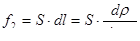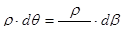После подстановки полученных значений площадей, приравняв слагаемые более высокого порядка к 0, получим:
(**)
напишем упрощенное уравнение пластичности
,
,
,
,
. (***)
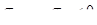После подставки (***) в (**), получим 
- дифференциальное уравнение 1-ого порядка с разделяющимися переменными. После интегрирования последнего выражения, получим
.
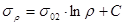Постоянная интегрирования С находится из условия:
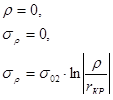
Если провести анализ с учетом трения, то схема действия сил на бесконечно малый элемент будет выглядеть следующим образом:
Считаем схему напряженного состояния плоской, но когда учитываем трение, то учитываем касательные напряжения. Напряжение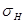 
суммируется по бесконечной образующей и становится соизмеримым с 
и 
и составляет 30-40%.
,
,
.
Зная эти напряжения, можно построить эпюры.
Дата добавления: 2019-07-15; просмотров: 266; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!