Гармонический ток при параллельном соединении RLC.

В соответствии с первым законом Кирхгофа для цепи с параллельным соединением R, L, C (рис. 6.4) имеем:

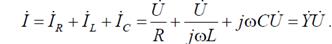
Ток в сопротивлении I_R совпадает по фазе с напряжением U; ток в индуктивности I _L отстает от напряжения на π/2; ток в емкости I _C опережает напряжение на π/2

Выражение   представляет собой комплексную проводимость цепи; g = 1/R – активная составляющая; b – реактивная составляющая проводимости цепи.

При ωL <1/ ωC проводимость цепи имеет индуктивный характер и полный ток I отстает от входного напряжения U по фазе (рис. 6.5, а).

При ωL >1/ ωC проводимость цепи имеет емкостный характер и полныйток I опережает входное напряжение Uпо фазе (рис. 6.5,б).

Активная составляющая тока I _A = I R , реактивная составляющая I _P = I _L + I _C и суммарный ток I образуют треугольник токов (рис. 6.6, а).

Если стороны треугольника токов поделить на входное напряжение, то получатся стороны треугольника проводимостей; для случая ωL <1/ ωC (рис. 6.6, б) и (рис. 6.6, в) для случая ωL >1/ ωC.

 

Мощность в цепи гармонического тока. Активная, реактивная и полная мощность.

Пусть имеем участок цепи R–X (рис. 7.1), находящийся под воздействи-

ем гармонического напряжения.

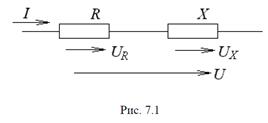
При напряжении на участке цепи u = Umcos ωt (ψ = 0) в цепи течет ток i = Imcos (ωt – φ).

Мгновенная мощность, поступающая в цепь

состоит из двух составляющих: постоянной величины и гармонической

, колеблющейся с удвоенной частотой.

На рис. 7.2 приведены временные диаграммы напряжения, тока и мгновенной мощности.

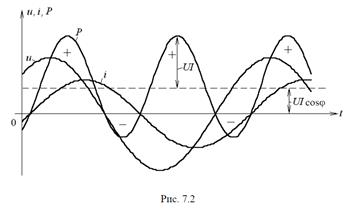
Выражение для мгновенной мощности может быть также представленов иной форме

Очевидно, что первое слагаемое является мгновенной скоростью расходования энергии в цепи, т. е. мощностью, потребляемой активным сопротивлением.

Второе слагаемое представляет собой мгновенную скорость запасания энергии в магнитном или электрическом поле цепи.

Активная мощность

Среднее значение мощности за период, равное активной мощности

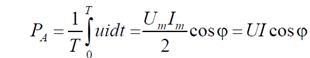
В отличие от цепи, содержащей только активное сопротивление, где

P _A = UI = RI², теперь P _A < UI.

Таким образом, активная мощность равна произведению действующих

значений напряжения и тока, умноженному на cos φ, который носит название

коэффициента мощности. Чем ближе угол φ к нулю, ближе cos φ к единице,

тем большая активная мощность будет передаваться от источника к нагрузке

при заданном напряжении.

Реактивная мощность

Мгновенная скорость запасания энергии – реактивная мощность – име-

ет абсолютное значение

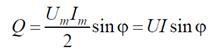
Знак Q свидетельствует о характере запасаемой энергии. Если Q > 0, то

энергия запасается в магнитном поле; если же Q < 0, энергия накапливается в электрическом поле цепи.

В отличие от чисто реактивной цепи, для которой , всмешанной цепи

Реактивная мощность измеряется в вольт-амперах реактивных (ВАР).

Реактивная мощность, подводимая к индуктивности,

где WL max – максимальное значение энергии магнитного поля, запасаемой в

индуктивности.

Реактивная мощность, подводимая к емкости

где WC max – максимальное значение энергии электрического поля, запасаемой

емкостью.

В цепи, содержащей индуктивность и емкость, реактивная мощность

Равна Q = ω(W_{L max} - W_{C max} )

 

Полная мощность

Величина, равная произведению действующих значений напряжения и тока на зажимах цепи S = UI, называется полной мощностью и измеряется в вольт-амперах (ВА).

Поскольку PA = UIcosφ = Scosφ, Q = UIsinφ = Ssinφ, то, очевидно

S² = PA ²+ Q² ; tgϕ = Q/PA

Энергетический расчет цепи гармонического тока может быть проведен и методом комплексных амплитуд, если воспользоваться следующим приемом.

Пусть через некоторое комплексное сопротивление Z под действием комплексной амплитуды напряжения

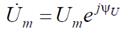
протекает ток с комплексной амплитудой

Найдем произведение из комплексной амплитуды напряженияи комплексного числа, сопряженного с комплексной амплитудой тока

Разделив полученное произведение на два, имеем

Таким образом, вещественная часть полученного произведения равнаактивной мощности PA, а мнимая часть реактивной мощности Q. На комплексной плоскости соотношение между мощностями может быть представлено в виде треугольника мощностей (рис. 7.3), подобного треугольнику сопротивлений.

Если комплексно-сопряженное напряжение умножить на комплексный ток и поделить полученное произведение на два, то получим:

Отсюда следует, что активная и реактивная мощности могут быть записаны в виде

Для комплексов действующих значений напряжения и тока

---

Дата добавления: 2019-07-15; просмотров: 530; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!