Замена переменной и интегрирование по частям в неопределенном интеграле.

Теоретические вопросы

Понятие первообразной функции. Теорема о первообразных.

Основной задачей дифференциального исчисления является нахождение производной f’( x) или дифференциала df= f’( x) dx функции f( x). В интегральном исчислении решается обратная задача. По заданной функции f( x) требуется найти такую функцию F( x), что F’(х)= f( x) или dF( x)= F’( x) dx= f( x) dx.

Таким образом, основной задачей интегрального исчисления является восстановление функции F( x) по известной производной (дифференциалу) этой функции. Интегральное исчисление имеет многочисленные приложения в геометрии, механике, физике и технике. Оно дает общий метод нахождения площадей, объемов, центров тяжести и т. д..

Определение. Функция F( x), , называется первообразной для функции f( x) на множестве Х, если она дифференцируема для любого и F’( x)= f( x) или dF( x)= f( x) dx.

Теорема. Любая непрерывная на отрезке [ a; b] функция f( x) имеет на этом отрезке первообразную F(x).

Теорема. Если F₁( x) и F₂( x) – две различные первообразные одной и той же функции f( x) на множестве х , то они отличаются друг от друга постоянным слагаемым, т. е. F₂( x)= F₁ x)+ C, где С – постоянная.

Неопределенный интеграл, его свойства.

Определение. Совокупность F( x)+ C всех первообразных функции f( x) на множестве Х называется неопределенным интегралом и обозначается:

- (1)

В формуле (1) f( x) dx называется подынтегральным выражением, f( x) – подынтегральной функцией, х – переменной интегрирования, а С – постоянной интегрирования.

Рассмотрим свойства неопределенного интеграла, вытекающие из его определения.

1. Производная из неопределенного интеграла равна подынтегральной функции, дифференциал неопределенного интеграла равен подынтегральному выражению:

и .

2. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной:

3. Постоянный множитель а (а≠0) можно выносить за знак неопределенного интеграла:

4. Неопределенный интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме интегралов от этих функций:

5. Если F( x) – первообразная функции f( x), то:

6 (инвариантность формул интегрирования). Любая формула интегрирования сохраняет свой вид, если переменную интегрирования заменить любой дифференцируемой функцией этой переменной:

где u – дифференцируемая функция.

Таблица неопределенных интегралов.

Приведем основные правила интегрирования функций.

II.

III.

IV.

VI.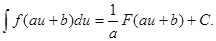

Приведем таблицу основных неопределенных интегралов. (Отметим, что здесь, как и в дифференциальном исчислении, буква u может обозначать как независимую переменную ( u= x), так и функцию от независимой переменной ( u= u( x)).)

1. ( n≠-1).

2. (a >0, a≠1).

10.

11.

12.

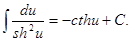
13.

14. (a≠0).

15. 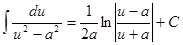(a≠0).

16. (|u| > |a|).

17. (|u| < |a|).

18.

19.

Интегралы 1 – 17 называют табличными.

Некоторые из приведенных выше формул таблицы интегралов, не имеющие аналога в таблице производных, проверяются дифференцированием их правых частей.

Замена переменной и интегрирование по частям в неопределенном интеграле.

Интегрирование подстановкой (замена переменной). Пусть требуется вычислить интеграл , который не является табличным. Суть метода подстановки состоит в том, что в интеграле переменную х заменяют переменной t по формуле x=φ( t), откуда dx=φ’( t) dt.

Теорема. Пусть функция x=φ( t) определена и дифференцируема на некотором множестве Т и пусть Х – множество значений этой функции, на котором определена функция f( x). Тогда если на множестве Х функция f( x) имеет первообразную, то на множестве Т справедлива формула:

- (2)

Формула (1) называется формулой замены переменной в неопределенном интеграле.

Интегрирование по частям. Метод интегрирования по частям следует из формулы дифференциала произведения двух функций. Пусть u( x) и v( x) – две дифференцируемые функции переменной х. Тогда:

d(uv)=udv+vdu. – (3)

Интегрируя обе части равенства (3), получаем:

Но так как , то:

- (4)

Соотношение (4) называется формулой интегрирования по частям. С помощью этой формулы отыскание интеграла . Применять ее целесообразно, когда интеграл в правой части формулы (4) более прост для вычисления, нежели исходный.

В формуле (4) отсутствует произвольная постоянная С, так как в правой части этой формулы стоит неопределенный интеграл, содержащий произвольную постоянную.

Приведем некоторые часто встречающиеся типы интегралов, вычисляемых методом интегрирования по частям.

I. Интегралы вида , , ( P_n( x) – многочлен степени n, k – некоторое число). Чтобы найти эти интегралы, достаточно положить u= P_n( x) и применить формулу (4) n раз.

II. Интегралы вида , , , , (Pn(x) – многочлен степени n относительно х). Их можно найти по частым, принимая за u функцию, являющуюся множителем при P_n( x).

III. Интегралы вида , (a, b – числа). Они вычисляются двукратным интегрированием по частям.

Дата добавления: 2019-07-15; просмотров: 321; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 4 5 6 Следующая ⇒

Мы поможем в написании ваших работ!