Разложение дробной рациональной функции на простейшие дроби.
Рациональной дробью R( x) называется дробь, числителем и знаменателем которой являются многочлены, т. Е. всякая дробь вида:
Если степень многочлена в числителе больше или равна степени многочлена в знаменателе ( n≥ m), то дробь называется неправильной. Если степень многочлена в числителе меньше степени многочлена в знаменателе ( n≤ m), то дробь называется правильной.
Всякую неправильную рациональную дробь можно представить в виде суммы многочлена (целой части) и правильной рациональной дроби (это представление достигается путем деления числителя на знаменатель по правилу деления многочленов):
где R( x) – многочлен-частное (целая часть) дроби 
; Pn( x) – остаток (многочлен степени n < m).
Интегрирование простейших дробей. Интегрирование рациональных дробей.
Интегрирование простейших дробей. Простейшей дробью называется правильная рациональная дробь одного из следующих четырех типов:
1) 
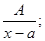
2) 
(n≥2);
3) 
4) 
(n≥2).
Здесь А, a, p, q, M, N – действительные числа, а трехчлен не имеет действительных корней, т. е. p2/4-q < 0.
Простейшие дроби первого и второго типов интегрируются непосредственно с помощью основных правил интегрального исчисления:
Интеграл от простейшей дроби третьего типа приводится к табличным интегралам путем выделения в числителе дифференциала знаменателя и приведения знаменателя к сумме квадратов:
|
|
|
Интегрирование рациональных дробей.
Разложение рациональной дроби на простейшие дроби. Всякую правильную рациональную дробь 
можно представить в виде суммы конечного числа простейших рациональных дробей первого – четвертого типов. Для разложения 
на простейшие дроби необходимо разложить знаменатель Qm( x) на линейные и квадратные множители, для чего надо решить уравнение:
- (5)
Теорема. Правильную рациональную дробь , где 
, можно единственным образом разложить на сумму простейших дробей:
- (6)
( A1, A2, …, Ak, B1, B2, …, B1, M1, N1, M2, M2, …, Ms, Ns – некоторые действительные числа).
Метод неопределенных коэффициентов. Суть метода неопределенных коэффициентов состоит в следующем. Пусть дано разложение правильной рациональной дроби по формуле (6) на простейшие дроби с неопределенными коэффициентами. Приведем простейшие дроби к общему знаменателю Qm( x) и приравняем многочлен, получившийся в числителе, многочлену Pn( x).
Метод частных значений. При нахождении неопределенных коэффициентов вместо того, чтобы сравнивать коэффициенты при одинаковых степенях х, можно дать переменной х несколько частных значений (по числу неопределенных коэффициентов) и получить таким образом систему уравнений относительно неопределенных коэффициентов. Особенно выгодно применять этот метод в случае, корни знаменателя рациональной дроби просты и действительны. Тогда оказывается удобным последовательно полагать равным каждому из корней знаменателя.
|
|
|
Правило интегрирования рациональных дробей . Для того чтобы проинтегрировать рациональную дробь, необходимо выполнить следующие действия:
1) если рассматриваемая рациональная дробь - неправильная ( k≥ m), представить ее в виде суммы многочлена и правильной рациональной дроби:
где n < m; R( x) – многочлен;
2) если рассматриваемая рациональная дробь - правильная ( n < m), представить ее в виде суммы простейших рациональных дробей по формуле (6);
3) интеграл от рациональной дроби представить в виде суммы интегралов от целой части и от соответствующих простейших дробей и вычислить эти интегралы.
Дата добавления: 2019-07-15; просмотров: 139; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!