Интегрирование выражений, содержащие тригонометрические функции.

Интегралы вида Универсальная подстановка. Будем рассматривать интегралы вида:

- (7)

при условии, что они не являются табличными. Вычислить их можно различными методами, изложенными ранее. Иногда бывает достаточно преобразовать подынтегральное выражение, использовав тригонометрические формулы, применить методы «подведения» множителя под знак дифференциала, замены переменной или интегрирования по частям.

Для вычисления интеграла вида (7) существует общая универсальная схема вычисления, основанная на универсальной тригонометрической подстановке .

Интегралы вида ( m, n є Z, m ≥ 0, n ≥ 0). Если хотя бы одно из чисел m и n – нечетное, то, отделяя от нечетной степени один сомножитель и выражая с помощью формулы sin² x+ cos² x=1 оставшуюся четную степень через конфункцию, приходим к табличному интегралу.

Интегралы вида , , ( n є N, n > 1). Эти интегралы вычисляются подстановками tgx= t и ctgx= t соответсвенно.

Если t= tgx, то x= arctgt, . Тогда:

Последний интеграл при n ≥ 2 является интегралом от неправильной рациональной дроби, которая вычисляется по правилу интегрирования рациональных дробей.

Аналогично если t= ctgx, то x= arcctgt, , откуда:

Интегралы вида ( m, n є R). Они вычисляются путем разложения подынтегральной функции на слагаемые по формулам:

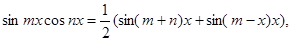
Интегрирование иррациональных выражений.

Интегралы вида (m₁, n₁, m₂, n₂, … - целые числа). В этих интегралах подынтегральная функция рациональна относительно переменной интегрирования и радикалов от х. Они вычисляются подстановкой x= t^s, где s – общий знаменатель дробей , , … При такой замене переменной все отношения = r₁, = r₂, … являются целыми числами, т. е. интеграл приводится к рациональной функции от переменной t:

Интегралы вида (m₁, n₁, m₂, n₂, … - целые числа). Эти интегралы подстановкой:

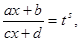
где s – общий знаменатель дробей , , …, сводятся к рациональной функции от переменной t.

Интегралы вида Для вычисления интеграла I₁ выделяется полный квадрат под знаком радикала:

и применяется подстановка:

, dx=du.

В результате этот интеграл сводится к табличному:

В числителе интеграла I₂ выделяется дифференциал выражения, стоящего под знаком радикала, и этот интеграл представляется в виде суммы двух интегралов:

где I₁ – вычисленный выше интеграл.

Вычисление интеграла I₃ сводится к вычислению интеграла I₁ подстановкой:

Интеграл вида Частные случаи вычисления интегралов данного вида рассмотрены в предыдущем пункте. Существует несколько различных приемов их вычисления. Рассмотрим один из таких приемов, основанный на применении тригонометрических подстановок.

Квадратный трехчлен ax²+ bx+ c путем выделения полного квадрата и замены переменной может быть представлен в виде Таким образом, достаточно ограничиться рассмотрением трех видов интегралов:

Интеграл подстановкой

u=ksint (или u=kcost)

сводится к интегралу от рациональной функции относительно sint и cost.

Интегралы вида (m, n, p є Q, a, b є R). Рассматриваемые интегралы, называемые интегралами от дифференциального бинома , выражаются через элементарные функции только в следующих трех случаях: