Понятие определенного интеграла, его геометрический смысл.
Определение. Если существует конечный передел интегральной суммы (8)
- (8)
при λ→0, не зависящий от способа разбиения τ n отрезка [ a; b] на частичные отрезки и выбора промежуточных точек ξ k, то этот предел называют определенным интегралом (или интегралом Римана) от функции f( x) на отрезке [ a; b] и обозначают:
Если указанный предел существует, то функция f( x) называется интегрируемой на отрезке [a; b] (или интегрируемой по Риману). При этом f( x) dx называется подынтегральным выражением, f( x) – подынтегральной функцией, х – переменной интегрирования, a и b – соответственно нижним и верхним пределами интегрирования.
Определенный интеграл есть число, равное пределу, к которому стремится интегральная сумма, в случае, когда диаметр разбиения λ стремится к нулю.
Геометрический смысл определенного интеграла. Пусть функция y= f( x) непрерывна на отрезке [a; b] и f( x) ≥ 0. Фигура, ограниченная графиком АВ функции y= f( x), прямыми x= a, x= b и осью Ох (рис. 1), называется криволинейной трапецией.
Интегральная сумма и ее слагаемые имеют простой геометрический смысл: произведение 
равно площади прямоугольника с основанием 
и высотой 
, а сумма 
представляет собой площадь заштрихованной ступенчатой фигуры (изображенной на рис. 1). Очевидно, что эта площадь зависит от разбиения τ n отрезка [a; b] на частичные отрезки и выбора точек ξ k.
|
|
|
Чем меньше 
, k=1, n, тем площадь ступенчатой фигуры ближе к площади криволинейной трапеции. Следовательно, за точную площадь S криволинейной трапеции принимается предел интегральной суммы при λ→0:
Таким образом, с геометрической точки зрения определенный интеграл от неотрицательной функции численно равен площади соответствующей криволинейной трапеции.
Основные свойства определенного интеграла.
Рассмотрим свойства определенного интеграла.
1. Если нижний и верхний пределы интегрирования равны ( a= b), то интеграл равен нулю:
Это свойство следует из определения интеграла.
2. Если f(x)=1, то
Действительно, так как f( x)=1, то
3. При перестановке пределов интегрирования определенный интеграл меняет знак на противоположный:
4. Постоянный множитель можно выносить за знак определенного интеграла:
R.
5. Определенный интеграл от алгебраической суммы конечного числа интегрируемых на [ a; b] функций f1( x), f2( x), …, fn( x) равен алгебраической сумме определенных интегралов от слагаемых:
6 (аддитивность определенного интеграла). Если существует интегралы 
и 
то существует также интеграл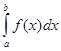 
и для любых чисел a, b, c;
|
|
|
7. Если f( x) ≥ 0 
[ a; b], то
a < b.
8 (определенность определенного интеграла). Если интегрируемые функции f( x) и φ( x) удовлетворяют неравенству f( x) ≥ φ( x) [ a; b], то
a > b.
9 (об оценке определенного интеграла). Если m и М – соответственно нименьшее и наибольшее значения функции f( x), непрерывной на отрезке [ a; b], то
a < b.
10 (теорема о среднем). Если функция f( x) непрерывна на отрезке [ a; b], то существует такая точка 
[ a; b], что
т. е. определенный интеграл от переменной функции равен произведению значения подынтегральной функции в некоторой промежуточной точке ξ отрезка интегрирования [ a; b] и длины b- a этого отрезка.
Теорема о среднем.
Если функция f( x) непрерывна на отрезке [ a; b], то существует такая точка 
[ a; b], что
т. е. определенный интеграл от переменной функции равен произведению значения подынтегральной функции в некоторой промежуточной точке ξ отрезка интегрирования [ a; b] и длины b- a этого отрезка.
Дата добавления: 2019-07-15; просмотров: 243; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!