Производная определенного интеграла по верхнему пределу. Формула Ньютона-Лейбница.
До сих пор мы рассматривали определенный интеграл с постоянными пределами интегрирования a и b. Если оставить постоянным нижний предел интегрирования a, а верхний х изменять так, чтобы x є [ a; b], то величина интеграла будет изменяться. Интеграл вида:
x є [a; b],
называется определенным интегралом с переменным верхним пределом и является функцией верхнего предела х. Здесь для удобства переменная интегрирования обозначена буквой t, а верхний предел интегрирования – буквой х.
Теорема. Производная определенного интеграла от непрерывной функции f( x) по его переменному верхнему пределу существует и равна подынтегральной функции, в которой вместо переменной интегрирования подставлено значение верхнего предела:
Формула Ньютона-Лейбница. Формула Ньютона-Лейбница дает правило вычисления определенного интеграла: значение определенного интеграла на отрезке [ a; b] от непрерывной функции f( x) равно разности значений любой ее первообразной, вычисленной при x= b и x= a.
- (9)
Замена переменной и интегрирования по частям в определенном интеграле.
Замена переменной в определенном интеграле. Этот метод, как и в случае неопределенного интеграла, позволяет упростить вычисления, т. е. привести подынтегральное выражение к соответствующей табличной форме. Применение замены переменной в определенном интеграле базируется на следующей теореме.
|
|
|
Теорема. Если функция f( x) непрерывная на отрезке [ a; b], а функция x=φ( t) непрерывно дифференцируема на отрезке [ t1; t2], причем φ([ t1; t2])=[ a; b] и φ( t1)= a, φ( t2)= b, то справедлива формула:
- (10)
Интегрирование по частям в определенном интеграле. Пусть u( x) и v( x) – дифференцируемые на отрезке [ a; b] функции переменной х. Тогда d( uv)= udv+ vdu. Проинтегрируем обе части последнего равенства на отрезке [a; b]:
- (11)
С другой стороны, по формуле Ньютона-Лейбница
Следовательно, формула (11) принимает вид:
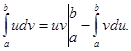- (12)
Формула (12) называется формулой интегрирования по частям в определенном интеграле.
Вычисление площадей плоских фигур.
Площадь криволинейной трапеции, ограниченной кривой y= f( x) [ f( x) ≥ 0], прямыми x= a и x= b и отрезками [ a; b] оси Ох, вычисляется по формуле:
Площадь фигуры, ограниченной кривыми y= f1( x) и y= f2( x)[ f1( x) ≤ f2( x)] и прямыми x= a и x= b, находится по формуле:
Если кривая задана параметрическими уравнениями x= x( t), y= y( t), то площадь криволинейной трапеции, ограниченной этой кривой, прямыми x= a, x= b и отрезком [ a; b] оси Ох, выражается формулой:
где t1 и t2 определяются из уравнений a= x( t1), b= x( t2) [ y( t) ≥ 0 при t1 ≤ t ≤ t2].
|
|
|
Площадь криволинейного сектора, ограниченного кривой, заданной в полярных координатах уравнением ρ=ρ(θ) и двумя полярными радиусами θ=α, θ=β (α < β), выражается интегралом:
Дата добавления: 2019-07-15; просмотров: 185; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!