Метод непосредственного интегрирования.
Определение. Непосредственным интегрированием называется интегрирование заключающееся в прямом применении формул таблицы основных интегралов. Чтобы найти неопределённый интеграл от какой–нибудь функции f(х), нужно прежде всего отыскать в таблице интегралов формулу в левой части которой стоит интеграл такого же вида, как данный, и записать ответ в соответствии с правой частью этой формулы.
Примеры.
1)
х7dх
Решение.
х7dх = + С
2)

2
3 х2 dх

Решение. Имеем 2
3 х2 dх = 2
х2/3dх
Применяя формулы, получаем 2
х2/3dх = 2
х2/3dх = 2 + С.

 Таким образом, 2х2/3dх = х 3 х2 + С.
Таким образом, 2х2/3dх = х 3 х2 + С.
3)
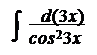
Решение. Согласно известному свойству дифференциала, 3
dх = d(
3х), а потому
=
Применяя формулу, получаем tg3х + С
В тех случаях, когда под знаком интеграла стоит алгебраическая сумма обычно разлагают данный интеграл на сумму нескольких интегралов, из которых каждый можно найти по соответствующей формуле.
3)


(2
х3 + 9
х2 – 5
х + 4/
х )
dх


Решение. (2
х3 + 9
х2 – 5
х + 4/
х )
dх =
 = 2 х3dх + 9 х2dх – 5 х1/2 + 4 dх/ х =
= 2 х3dх + 9 х2dх – 5 х1/2 + 4 dх/ х =

= 2 + 9 – 5 + 4 * 2
х + С =

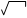 = х4 / 2 + 3х3 – 10/3 х х + 8 х + С.
= х4 / 2 + 3х3 – 10/3 х х + 8 х + С.
Метод замены переменной (способ подстановки).
Наиболее общим приёмом интегрирования функций является способ подстановки, который применяется тогда, когда искомый интеграл
f(
х)
dх не является табличным, но путём но путём ряда элементарных преобразований он может быть сведён к табличному.
Метод подстановки основан на применении следующей формулы:
f(х)dх = f[j(t)]j’(t)dt, (1)
где х = j(t) – дифференцируемая функция от t, производная которой j’(t) сохраняет знак для рассматриваемых значений переменных.
Сущность применения этой формулы состоит в том, что в данном интеграле
f(
х)
dх переменная
х заменяется переменной
t по формуле
х = j(
t) и, следовательно,
dх произведением j’(
t)
dt.
Справедливость формулы (1) будет доказана если после дифференцирования обеих её частей получатся одинаковые выражения. Продифференцировав левую часть формулы, имеем
d [ f(х)dх ] = f(х)dх = f [j(t)] j’(t)dt
Продифференцировав правую часть формулы, имеем
d f [j(t)] j’(t)dt = f [ j(t) ] j’(t)dt
Таким образом, формула (1) справедлива. Часто употребляется обратная замена переменной, то есть, подстановка t = j(t), dt = j’(t)dх.
Примеры.
1) (2х + 3)4dх.
Данный интеграл можно свести к табличному интегралу (V). Подстановка выбирается из простого соображения: в подынтегральном выражении табличного интеграла (V) в основании степени и под знаком дифференциала стоит одно и тоже выражение и.
Следовательно, в данном случае нужно применить подстановку
и = 2
х + 3, отсюда имеем
dи = 2
dх и
dх =
dи/2
, а потому
(2
х + 3)
4dх =
и4(
dи/2) = 1/2
и4dи =
= 1/2 * и5/5 + С = + С.
Интегрирование по частям.
Допустим, что u, v – функции переменной х, непрерывные и имеющие производные в интервале (а,в). имеем тогда
(uv)’ = uv’ + vu’
так что uv’ = (uv)’ – vu’
Беря неопределённые интегралы от обоих частей и учитывая, что
uv’dх =
uv –
vu’dх, (1)
Если оба интеграла существуют.
Пользуясь дифференциалами предыдущую формулу можно написать в следующем виде:
udv = uv – vdu. (2)
Формула (2) даёт возможность вычисления интеграла
udv свести к вычислению интеграла
vdu , который, быть может, берётся легче. Этот метод называется интегрированием по частям.
Примеры.
1) J = хехdх.
Положим
и = х, dи = dх, dv = ехdх,
v = ехdх = ех
Следовательно,
J = хех – ехdх = хех – ех + С.
2)
ln хdх .
Положим, u = ln х, dи = dх/х
dv = dх v = dх = х.
Следовательно,
J = х ln х – dх = х ln х – х + С..
Дата добавления: 2019-07-15; просмотров: 209; | Поделиться с друзьями:
|

Мы поможем в написании ваших работ!
 2 3 х2 dх
2 3 х2 dх
 Решение. Имеем 2 3 х2 dх = 2х2/3dх
Решение. Имеем 2 3 х2 dх = 2х2/3dх

 Таким образом, 2х2/3dх = х 3 х2 + С.
Таким образом, 2х2/3dх = х 3 х2 + С.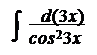 Решение. Согласно известному свойству дифференциала, 3dх = d(3х), а потому
Решение. Согласно известному свойству дифференциала, 3dх = d(3х), а потому

 (2х3 + 9х2 – 5 х + 4/ х )dх
(2х3 + 9х2 – 5 х + 4/ х )dх

 Решение. (2х3 + 9х2 – 5 х + 4/ х )dх =
Решение. (2х3 + 9х2 – 5 х + 4/ х )dх =
 = 2 х3dх + 9 х2dх – 5 х1/2 + 4 dх/ х =
= 2 х3dх + 9 х2dх – 5 х1/2 + 4 dх/ х =

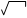 = х4 / 2 + 3х3 – 10/3 х х + 8 х + С.
= х4 / 2 + 3х3 – 10/3 х х + 8 х + С.
