Замены переменных в определённых интегралах.

⇐ ПредыдущаяСтр 7 из 10Следующая ⇒

Пусть требуется в определённом интеграле

f(х)dх

применить подстановку х = j(t). Тогда имеет место следующая формула замены переменных в определённом интеграле:

f(х)dх = f [j(t)]j’(t)dt,

где j(a) = а, j(b) = в.

Эту формулу мы докажем при условиях:

1. Функции j(t) и j’(t) непрерывны в [a, b].

2. Функция f(х) определена и непрерывна для всех значений, которые функция х = j(t) принимает в [a, b].

3. j(a) = а, j(b) = в.

Доказательство: Обозначим через М и т наибольшее и наименьшее значения функции х = j(t) в [a, b]. Пусть

F(х) = f(х)dх, т £ х £ М.

По теореме о подстановке в неопределённых интегралах для всех t из [a, b] справедливо равенство

F[j(t)] = f[j(t)]j’(t)dt.

Отсюда f[j(t)]j’(t)dt = F[j(b)] – F[j(a)] = F(в) – F(а)

Так как f(х)dх = F(в) – F(а)

то из сравнения последних двух равенств получим доказываемую формулу.

Пример. Вычислить интеграл

J = х 1+х² dх

^Ö ² ¹

Подставим 1+х² = t, то есть, х = t² –1 . Имеем: t = 1, при х =0, t = Ö2, при х = 1. Так как dх = tdt/ t² –1 , то

J = t²dt = t³/3| = (2Ö2 – 1)/3.

Интегрирование по частям.

Пусть функции f(х) и j(х) непрерывны вместе со своими производными в интервале [а,в]. Пусть, далее,

F(х) = f(х) j(х).

Тогда F’(х) = f(х) j’(х) f’(х) j(х).

^в ^а

Так как F’(х)dх = F(х)| ,

^в ^а

то [f(х) j’(х) f’(х) j(х)]dх = f(х) j(х)| ,

откуда f(х) j’(х)dх = f(х) j(х)| – f’(х) j(х)dх

Примеры.

1) Вычислить интеграл.

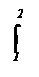х cos х dх

^в ^а

Положив f(х) = х, j(х) = sin х получим:

х cos х dх = х sin х| – sin х dх = –2

2) Вычислить интеграл

ln х dх.

²¹

Положив f(х) = ln х, j(х) = х получим:

²¹

ln х dх = [х ln х] – х(dх/х) =

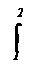
= [х ln х] – [х] = 2 ln2 – 1 = ln4 – 1

Исторические сведения о возникновении и развитии основных понятий.

В математике XVII в. самым большим достижением справедливо считается изобретение дифференциального и интегрального исчисления. Сформировалось оно в ряде сочинений Ньютона и Лейбница и их ближайших сотрудников и учеников. Введение в математику методов анализа бесконечно малых стало началом больших преобразований, быстро изменивших всё лицо математики и поднявших её роль в системе естественно научных знаний человечества.

Однако появление анализа бесконечно малых не было делом рук одного или нескольких учёных, их гениальной догадки. Оно в действительности было завершением длительного процесса, внутриматематическая сущность которого состояла в накоплении и выделении элементов дифференциального и интегрального исчисления и теории рядов.

Для создания исчисления бесконечно малых внутри математики XVII в. сложились достаточные предпосылки. Это были: наличие сложившейся алгебры и вычислительной техники; введение в математику переменной величины и координатного метода; усвоение инфинитезимальных идей древних, особенно Архимеда; накопление методов решения задач на вычисление квадратур, кубатур, определение центров тяжести, нахождение касательных, экстремалей и т.д.

Дата добавления: 2019-07-15; просмотров: 166; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 4 5 678 9 10 Следующая ⇒

Мы поможем в написании ваших работ!